Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jaka figurę otrzymamy, łącząc kolejno środki boków: a) rombu, b) prostokąta, c) kwadratu?
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Udowodnij...
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
Trapez równoramienny 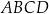 nie jest równoległobokiem. Przekątna
nie jest równoległobokiem. Przekątna 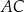 tego trapezu tworzy z podstawą
tego trapezu tworzy z podstawą 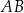 kąt o mierze
kąt o mierze 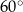 . Wykaż, że trapez
. Wykaż, że trapez 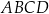 nie może być opisany na okręgu.
nie może być opisany na okręgu.
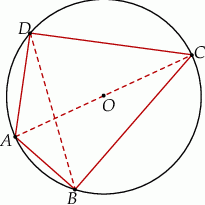
Czworokąt 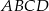 jest wpisany w okrąg oraz pola trójkątów
jest wpisany w okrąg oraz pola trójkątów 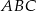 i
i 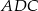 są równe. Wykaż, że
są równe. Wykaż, że
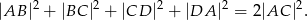
Dwa przeciwległe boki czworokąta wpisanego w okrąg mają równe długości. Wykaż, że czworokąt ten jest trapezem.
Dany jest czworokąt wypukły 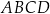 . Przekątne
. Przekątne 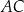 oraz
oraz 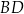 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 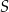 . Wykaż, że jeżeli
. Wykaż, że jeżeli 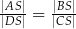 , to na czworokącie
, to na czworokącie 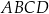 można opisać okrąg.
można opisać okrąg.
Dany jest czworokąt wypukły 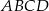 , w którym:
, w którym: 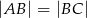 ,
, 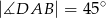 ,
, 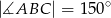 ,
, 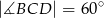 . Wykaż, że trójkąt
. Wykaż, że trójkąt 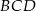 jest równoboczny.
jest równoboczny.
Przekątne czworokąta wypukłego 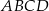 dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt
dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt 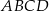 można wpisać okrąg.
można wpisać okrąg.
Przez każde dwa sąsiednie wierzchołki czworokąta 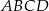 wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
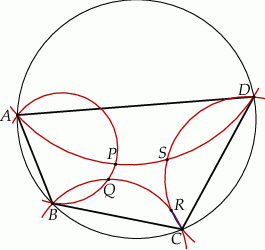
Wykaż, że punkty 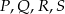 , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
Dany jest czworokąt 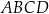 . Niech
. Niech 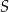 będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt
będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt 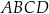 można wpisać w okrąg wtedy i tylko wtedy, gdy
można wpisać w okrąg wtedy i tylko wtedy, gdy 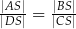 .
.
Bok 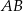 czworokąta
czworokąta 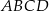 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 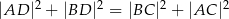 .
.
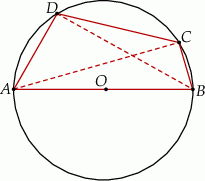
Przekątna 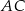 czworokąta
czworokąta 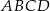 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 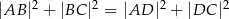 .
.