Bok kwadratu 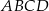 ma długość 1. Na bokach
ma długość 1. Na bokach 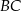 i
i 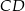 wybrano odpowiednio punkty
wybrano odpowiednio punkty 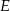 i
i 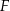 umieszczone tak, by
umieszczone tak, by 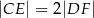 . Oblicz wartość
. Oblicz wartość 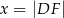 , dla której pole trójkąta
, dla której pole trójkąta 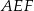 jest najmniejsze.
jest najmniejsze.
/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema
Dany jest kwadrat 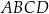 o boku długości 2. Na bokach
o boku długości 2. Na bokach 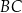 i
i 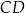 tego kwadratu wybrano – odpowiednio – punkty
tego kwadratu wybrano – odpowiednio – punkty 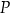 i
i 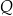 , takie, że długość odcinka
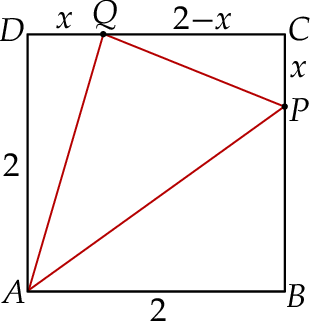
, takie, że długość odcinka 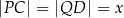 (zobacz rysunek). Wyznacz tę wartość
(zobacz rysunek). Wyznacz tę wartość  , dla której pole trójkąta
, dla której pole trójkąta 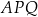 osiąga wartość najmniejszą. Oblicz to najmniejsze pole.
osiąga wartość najmniejszą. Oblicz to najmniejsze pole.
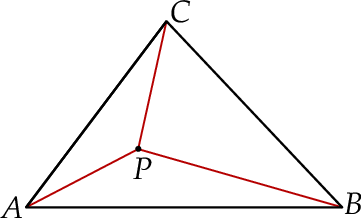
Każdy kąt trójkąta 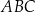 ma miarę mniejszą od
ma miarę mniejszą od 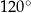 . Wyznacz taki punkt
. Wyznacz taki punkt 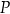 wewnątrz trójkąta
wewnątrz trójkąta 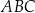 , dla którego suma
, dla którego suma 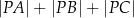 jest najmniejsza możliwa.
jest najmniejsza możliwa.
Heron codziennie rano wyrusza ze swojego domu (punkt 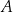 ) do brzegu rzeki (prosta
) do brzegu rzeki (prosta 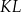 ) aby nabrać wodę (w punkcie
) aby nabrać wodę (w punkcie 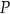 ) i podlać rośliny w sadzie (punkt
) i podlać rośliny w sadzie (punkt 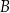 ).
).
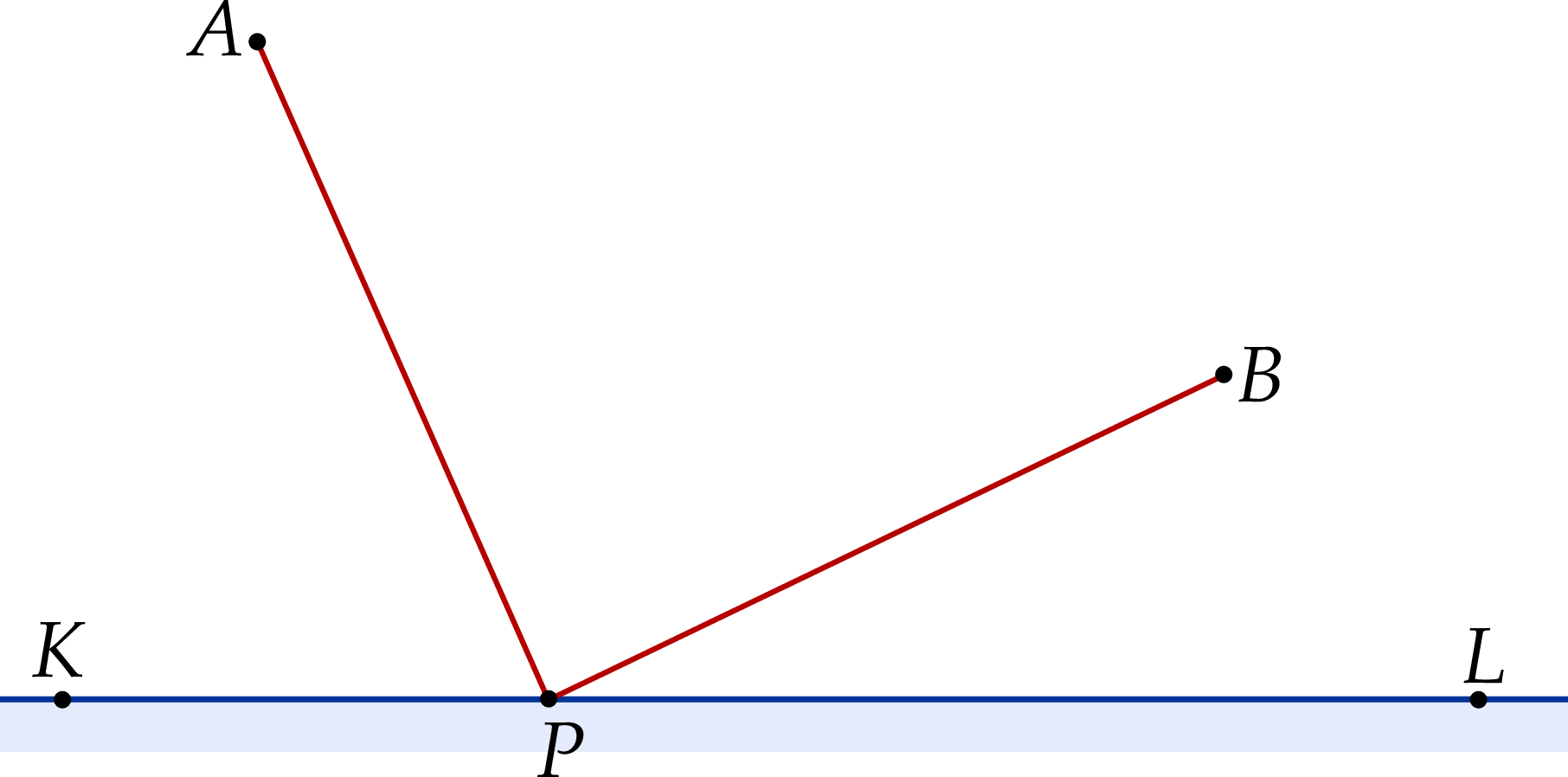
Jakie powinno być położenie punktu 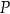 , żeby pokonana przez niego droga (wzdłuż łamanej
, żeby pokonana przez niego droga (wzdłuż łamanej 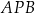 ) była najkrótsza?
) była najkrótsza?
W trójkącie o obwodzie 14 jeden z boków jest dwa razy dłuższy od drugiego boku. Oblicz cosinus najmniejszego kąta, tego spośród trójkątów spełniających podany warunek, w którym suma kwadratów długości boków jest najmniejsza.
Na kole o promieniu 4 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta, którego pole jest najmniejsze.
Na kole o promieniu 12 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta, którego pole jest najmniejsze.
Na kole o promieniu 1 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta, którego pole jest najmniejsze.
Obwód trapezu równoramiennego kącie ostrym 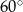 równa się
równa się 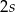 (
(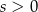 ). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole.
). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole.
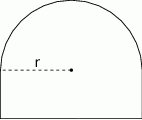
Z arkusza blachy w kształcie półkola o promieniu 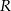 należy wyciąć trapez, którego jedna podstawa jest średnicą tego półkola, a wierzchołki drugiej podstawy leżą na jego brzegu (zobacz rysunek).
należy wyciąć trapez, którego jedna podstawa jest średnicą tego półkola, a wierzchołki drugiej podstawy leżą na jego brzegu (zobacz rysunek).
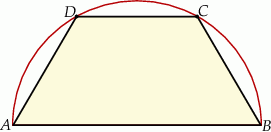
Oblicz jaką długość powinno mieć ramię tego trapezu, aby jego pole było największe możliwe. Oblicz to pole.
Dany jest trójkąt równoboczny 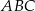 o boku długości
o boku długości  . Punkty
. Punkty 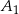 ,
, 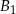 i
i 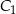 należą do boków
należą do boków 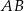 ,
, 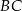 i
i 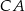 , przy czym
, przy czym 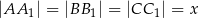 .
.
- Wyraź pole trójkąta
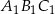 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji.
. Wyznacz dziedzinę tej funkcji. - Wyznacz wartość
 , dla której pole trójkąta
, dla której pole trójkąta 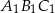 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.
Drut o długości 72 cm rozcięto na dwa kawałki i z każdego kawałka zbudowano brzeg trójkąta równoramiennego, przy czym stosunek długości ramienia do długości podstawy w jednym trójkącie wynosi 5:8, a w drugim 13:10. Jakie obwody mają te trójkąty jeżeli suma ich pól jest najmniejsza z możliwych?
Spośród wszystkich trapezów, w których iloczyn długości podstaw jest równy 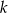 , a pole jest równe
, a pole jest równe 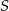 wybrano ten, który ma najdłuższą wysokość. Wykaż, że przekątne wybranego trapezu dzielą się na połowy.
wybrano ten, który ma najdłuższą wysokość. Wykaż, że przekątne wybranego trapezu dzielą się na połowy.
W kwadracie 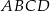 o boku długości 1 na boku
o boku długości 1 na boku 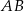 wybrano punkt
wybrano punkt 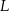 . Na bokach
. Na bokach 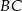 i
i 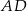 wybrano odpowiednio punkty
wybrano odpowiednio punkty 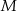 i
i 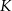 tak, że
tak, że 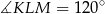 , a dwusieczna tego kąta jest równoległa do boku
, a dwusieczna tego kąta jest równoległa do boku 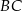 . Oblicz długości odcinków
. Oblicz długości odcinków 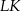 i
i 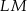 , dla których pole trójkąta
, dla których pole trójkąta 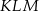 jest największe.
jest największe.
Rozpatrujemy wszystkie trójkąty równoramienne o obwodzie równym 18.
- Wykaż, że pole
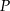 każdego z tych trójkątów, jako funkcja długości
każdego z tych trójkątów, jako funkcja długości 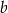 ramienia, wyraża się wzorem
ramienia, wyraża się wzorem 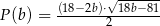 .
. - Wyznacz dziedzinę funkcji
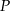 .
. - Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole.
Działka ma kształt trapezu. Podstawy 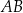 i
i 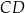 tego trapezu mają długości
tego trapezu mają długości 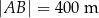 oraz
oraz 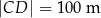 . Wysokość trapezu jest równa 75 m, a jego kąty
. Wysokość trapezu jest równa 75 m, a jego kąty 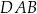 i
i 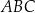 są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie
są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie 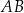 tego trapezu, a dwa pozostałe –
tego trapezu, a dwa pozostałe – 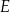 oraz
oraz 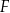 – na ramionach
– na ramionach 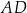 i
i 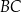 trapezu (zobacz rysunek).
trapezu (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię.
Działka ma kształt trapezu. Podstawy 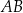 i
i 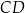 tego trapezu mają długości
tego trapezu mają długości 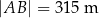 oraz
oraz 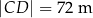 . Wysokość trapezu jest równa 54 m, a jego kąty
. Wysokość trapezu jest równa 54 m, a jego kąty 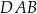 i
i 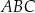 są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie
są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie 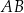 tego trapezu, a dwa pozostałe –
tego trapezu, a dwa pozostałe – 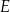 oraz
oraz 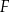 – na ramionach
– na ramionach 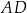 i
i 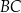 trapezu (zobacz rysunek).
trapezu (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię.
Budżet przeznaczony na ogrodzenie pewnej działki w kształcie trójkąta równoramiennego 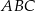 (
(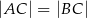 ) wynosi 12 000 zł.
) wynosi 12 000 zł.
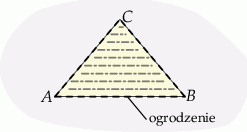
Ze względu na warunki terenowe, koszt wykonania 1 metra bieżącego ogrodzenia jest różny dla każdego z boków trójkąta 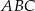 i wynosi odpowiednio: 140 zł dla boku
i wynosi odpowiednio: 140 zł dla boku 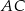 , 100 zł dla boku
, 100 zł dla boku 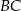 i 360 zł dla boku
i 360 zł dla boku 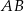 . Oblicz jakie powinny być wymiary ogrodzenia, aby odgradzało ono działkę o największym możliwym polu powierzchni. Wymiary podaj z dokładnością do 1 metra.
. Oblicz jakie powinny być wymiary ogrodzenia, aby odgradzało ono działkę o największym możliwym polu powierzchni. Wymiary podaj z dokładnością do 1 metra.
Rozpatrujemy wszystkie trójkąty prostokątne 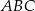 o przeciwprostokątnej
o przeciwprostokątnej 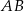 i obwodzie równym 4. Niech
i obwodzie równym 4. Niech 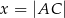 .
.
- Wykaż, że pole
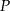 trójkąta
trójkąta 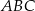 jako funkcja zmiennej
jako funkcja zmiennej  jest określone wzorem
jest określone wzorem 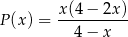
- Wyznacz dziedzinę funkcji
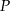 .
. - Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
Rozpatrujemy wszystkie prostokąty 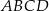 , w których suma długości dwóch sąsiednich boków i przekątnej jest równa 6. Niech
, w których suma długości dwóch sąsiednich boków i przekątnej jest równa 6. Niech 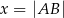 .
.
- Wykaż, że pole
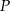 prostokąta
prostokąta 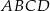 jako funkcja zmiennej
jako funkcja zmiennej  jest określone wzorem
jest określone wzorem 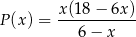
- Wyznacz dziedzinę funkcji
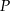 .
. - Oblicz długości boków tego z rozpatrywanych prostokątów, który ma największe pole. Oblicz to największe pole.
W trójkąt prostokątny 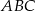 , w którym
, w którym 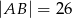 ,
, 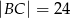 ,
, 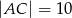 , wpisujemy prostokąty
, wpisujemy prostokąty 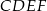 , tak, że punkt
, tak, że punkt 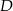 należy do boku
należy do boku 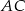 , pkt
, pkt 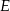 należy do boku
należy do boku 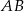 i punkt
i punkt 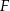 należy do boku
należy do boku 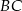 . Oblicz wymiary prostokąta o największym polu.
. Oblicz wymiary prostokąta o największym polu.
Przedstawiona na rysunku figura składa się z półkola i prostokąta. Oblicz maksymalne pole tej figury, jeżeli jej obwód jest równy 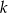 .
.
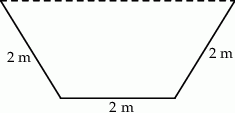
Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 4 dm. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby do pomieszczenia wpadało przez to okno jak najwięcej światła, czyli aby pole powierzchni okna było największe. Oblicz to pole.
Rozważamy zbiór wszystkich trapezów równoramiennych, których krótsza podstawa i ramiona mają długość 6. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby jego pole było największe. Oblicz to pole.
Betonowy kanał wodny ma mieć przekrój w kształcie trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 2 m. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby przez kanał mogło przepłynąć jak najwięcej wody, czyli aby pole powierzchni przekroju kanału było największe. Oblicz to pole przekroju.
Długości boków prostokąta 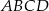 spełniają warunki:
spełniają warunki: 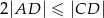 i
i 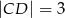 . Na boku
. Na boku 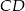 wybrano punkty
wybrano punkty 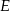 i
i 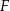 w ten sposób, że
w ten sposób, że 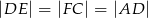 . Punkt
. Punkt 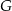 jest takim punktem odcinka
jest takim punktem odcinka 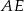 , że
, że 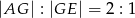 . Oblicz długość boku
. Oblicz długość boku 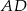 prostokąta, dla której pole trójkąta
prostokąta, dla której pole trójkąta 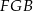 jest największe.
jest największe.
Dany jest romb 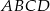 o boku długości 1, w którym kąt
o boku długości 1, w którym kąt 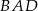 jest ostry i
jest ostry i 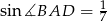 . Na bokach
. Na bokach 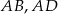 i
i 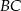 wybrano odpowiednio punkty
wybrano odpowiednio punkty 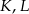 i
i 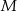 w ten sposób, że odcinki
w ten sposób, że odcinki 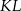 i
i 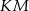 są równoległe do przekątnych rombu.
są równoległe do przekątnych rombu.
- Oblicz pole czworokąta
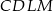 .
. - Oblicz największą możliwą wartość pola trójkąta
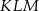 .
.

