Na bokach 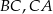 i
i 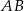 trójkąta
trójkąta 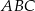 wybrano punkty
wybrano punkty 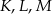 takie, że
takie, że
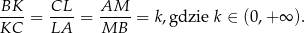
Wyznacz wartość 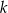 , dla której stosunek pola trójkąta
, dla której stosunek pola trójkąta  do pola trójkąta
do pola trójkąta  jest najmniejszy.
jest najmniejszy.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na bokach 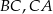 i
i 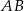 trójkąta
trójkąta 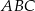 wybrano punkty
wybrano punkty 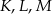 takie, że
takie, że
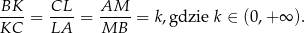
Wyznacz wartość 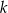 , dla której stosunek pola trójkąta
, dla której stosunek pola trójkąta 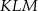 do pola trójkąta
do pola trójkąta 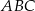 jest najmniejszy.
jest najmniejszy.
Wyznacz wymiary prostokąta o obwodzie 36 cm, którego pole jest największe.
Z drutu o długości 320 cm zbudowano ramkę w kształcie prostokąta. Jakie powinna mieć wymiary aby pole prostokąta było największe?
Z drutu o długości 200 cm zbudowano ramkę w kształcie prostokąta. Jakie powinna mieć wymiary aby pole prostokąta było największe?
Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego przekątna ma długość 6 dm. Oblicz, jakie jest największe możliwe pole powierzchni tego okna.
Rozpatrujemy trapezy równoramienne  o przekątnej długości 1 i sumie długości podstaw równej
o przekątnej długości 1 i sumie długości podstaw równej  . Zapisz pole trapezu
. Zapisz pole trapezu  jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.
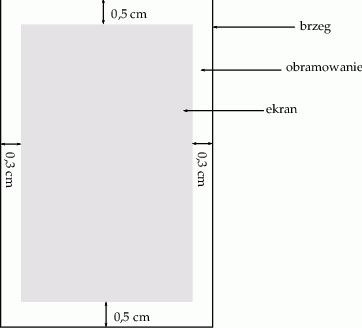
Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego ekranu od krótszych brzegów smartfona były równe 0,5 cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe 0,3 cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię 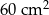 . Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
. Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
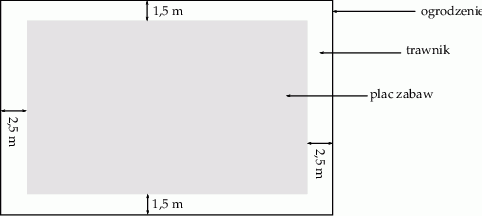
Należy zaprojektować wymiary prostokątnego placu zabaw, tak aby szerokość trawnika wzdłuż dłuższych brzegów placu była równa 1,5 m, a szerokość trawnika wzdłuż krótszych brzegów placu była równa 2,5 m (zobacz rysunek – plac zabaw zaznaczono kolorem szarym). Sam plac zabaw ma mieć powierzchnię 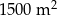 . Wyznacz takie wymiary placu zabaw, przy których powierzchnia placu wraz z trawnikami jest najmniejsza.
. Wyznacz takie wymiary placu zabaw, przy których powierzchnia placu wraz z trawnikami jest najmniejsza.
Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, spełniające warunek: suma długości dłuższej podstawy  i wysokości trapezu jest równa 2.
i wysokości trapezu jest równa 2.
 , dla których istnieje trapez o podanych własnościach.
, dla których istnieje trapez o podanych własnościach.  takiego trapezu, jako funkcja długości
takiego trapezu, jako funkcja długości  dłuższej podstawy trapezu, wyraża się wzorem
dłuższej podstawy trapezu, wyraża się wzorem 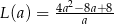
Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, i w których suma długości dłuższej podstawy i średnicy okręgu wpisanego jest równa 6. Wyznacz wymiary tego spośród tych trapezów, który ma najmniejszy obwód. Oblicz ten obwód.
Oblicz jakie długości powinny mieć boki prostokąta o polu równym 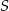 , aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
, aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
Suma długości dwóch boków trójkąta jest równa 4, a kąt zawarty między nimi ma miarę 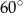 . Oblicz najmniejszą możliwą wartość obwodu trójkąta.
. Oblicz najmniejszą możliwą wartość obwodu trójkąta.
Suma długości dwóch boków trójkąta wynosi 6 cm, a miara kąta pomiędzy tymi bokami wynosi 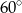 . Jaką najmniejszą wartość ma obwód tego trójkąta.
. Jaką najmniejszą wartość ma obwód tego trójkąta.
 i
i 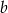 spełniona jest nierówność
spełniona jest nierówność 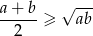
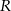 znajdź prostokąt o największym polu.
znajdź prostokąt o największym polu.Dany jest okrąg o środku 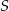 i promieniu 18. Rozpatrujemy pary okręgów: jeden o środku
i promieniu 18. Rozpatrujemy pary okręgów: jeden o środku 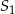 i promieniu
i promieniu  oraz drugi o środku
oraz drugi o środku 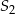 i promieniu
i promieniu 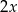 , o których wiadomo, że spełniają jednocześnie następujące warunki:
, o których wiadomo, że spełniają jednocześnie następujące warunki:
– rozważane dwa okręgi są styczne zewnętrznie;
– obydwa rozważane okręgi są styczne wewnętrznie do okręgu o środku 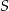 i promieniu 18;
i promieniu 18;
– punkty: 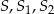 nie leżą na jednej prostej.
nie leżą na jednej prostej.
Pole trójkąta o bokach 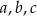 można obliczyć ze wzoru Herona
można obliczyć ze wzoru Herona
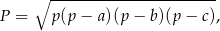
gdzie 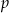 – jest połową obwodu trójkąta.
– jest połową obwodu trójkąta.
Zapisz pole trójkąta 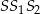 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
Dany jest okrąg o środku 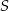 i promieniu 12. Rozpatrujemy pary okręgów: jeden o środku
i promieniu 12. Rozpatrujemy pary okręgów: jeden o środku 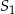 i promieniu
i promieniu  oraz drugi o środku
oraz drugi o środku 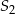 i promieniu
i promieniu 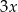 , o których wiadomo, że spełniają jednocześnie następujące warunki:
, o których wiadomo, że spełniają jednocześnie następujące warunki:
– rozważane dwa okręgi są styczne zewnętrznie;
– obydwa rozważane okręgi są styczne wewnętrznie do okręgu o środku 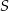 i promieniu 12;
i promieniu 12;
– punkty: 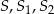 nie leżą na jednej prostej.
nie leżą na jednej prostej.
Zapisz pole trójkąta 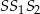 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
Rozważamy wszystkie trapezy równoramienne o obwodzie równym 96 i kącie ostrym o mierze 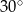 .
.
 jego ramienia.
jego ramienia. Cztery miasta 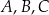 i
i 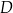 znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami
znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami 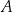 i
i 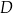 , a drugi węzeł z miastami
, a drugi węzeł z miastami  i
i  (zobacz rysunek).
(zobacz rysunek).
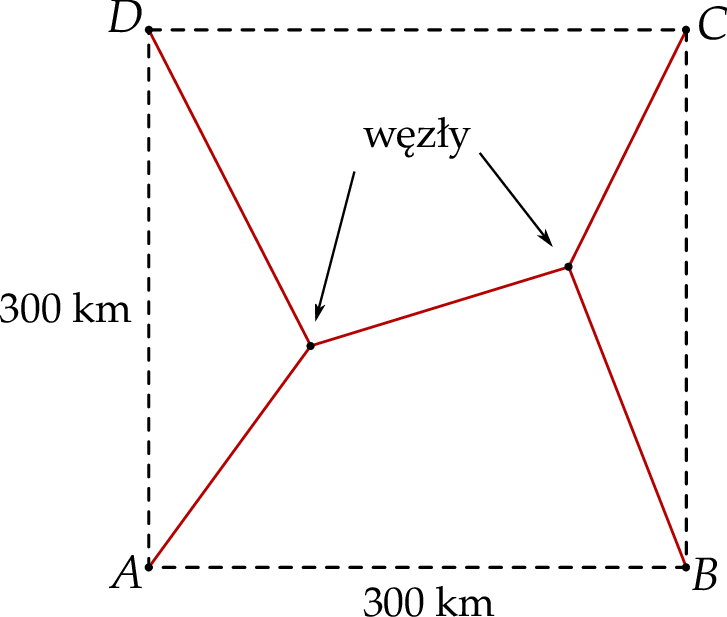
Oblicz, jaka musi być długość najkrótszej takiej sieci dróg i gdzie muszą być zlokalizowane węzły tej sieci.
W trójkąt prostokątny o przyprostokątnych długości 6 i 8 wpisujemy prostokąt w taki sposób, że dwa jego boki zawarte są w przyprostokątnych, a jeden z jego wierzchołków leży na przeciwprostokątnej. Zbadaj, jakie powinny być wymiary prostokąta, aby jego pole było możliwie największe.
Dany jest odcinek  o długości 10. Rozpatrujemy wszystkie sześciokąty foremne
o długości 10. Rozpatrujemy wszystkie sześciokąty foremne 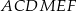 i trójkąty równoboczne
i trójkąty równoboczne 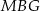 , których wspólny wierzchołek
, których wspólny wierzchołek 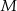 leży na odcinku
leży na odcinku 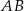 (zobacz rysunek).
(zobacz rysunek).
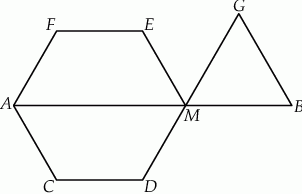
Oblicz stosunek obwodu sześciokąta  do obwodu trójkąta
do obwodu trójkąta  w przypadku, gdy suma pól tych dwóch wielokątów jest najmniejsza.
w przypadku, gdy suma pól tych dwóch wielokątów jest najmniejsza.
Z odcinka drutu o długości 4 m wykonano ramkę w kształcie rombu z jedną przekątną (zobacz rysunek).
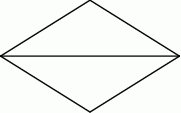
Jaka powinna być długość tej przekątnej, aby pole powierzchni tego rombu było największe możliwe?
Suma długości dwóch sąsiednich boków w pewnym trójkącie jest równa 14, a kąt między tymi bokami ma miarę 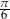 . Wyznacz długości boków trójkąta tak, aby jego pole było największe. Oblicz pole tego trójkąta.
. Wyznacz długości boków trójkąta tak, aby jego pole było największe. Oblicz pole tego trójkąta.
W trójkąt prostokątny o kącie ostrym 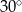 i przeciwprostokątnej długości 40 cm wpisujemy prostokąty w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w przeciwprostokątnej trójkąta. Zbadaj który z tych prostokątów ma największe pole.
i przeciwprostokątnej długości 40 cm wpisujemy prostokąty w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w przeciwprostokątnej trójkąta. Zbadaj który z tych prostokątów ma największe pole.
Oblicz jaka może być najmniejsza możliwa długość przeciwprostokątnej trójkąta prostokątnego o polu 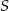 .
.
Na bokach prostokąta o obwodzie 16 cm opisano, jako na średnicach, półokręgi leżące na zewnątrz prostokąta. Zbadaj, dla jakich długości boków prostokąta, pole figury ograniczonej krzywą złożoną z tych czterech półokręgów jest najmniejsze. Oblicz to pole
Wewnątrz prostokąta  o wymiarach
o wymiarach 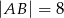 i
i 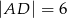 wybrano dwa punkty
wybrano dwa punkty 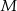 i
i 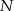 takie, że
takie, że 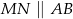 oraz
oraz 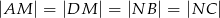 . Przy jakiej odległości punktów
. Przy jakiej odległości punktów 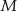 i
i 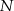 suma kwadratów długości odcinków
suma kwadratów długości odcinków 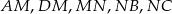 jest najmniejsza?
jest najmniejsza?
Arkusz blachy ma kształt trójkąta prostokątnego 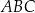 , w którym
, w którym 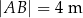 i
i 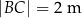 . Z tego arkusza należy wyciąć trójkąt równoramienny
. Z tego arkusza należy wyciąć trójkąt równoramienny 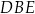 w ten sposób, że punkty
w ten sposób, że punkty 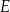 i
i 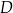 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 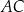 i
i 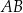 oraz
oraz 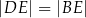 (zobacz rysunek).
(zobacz rysunek).
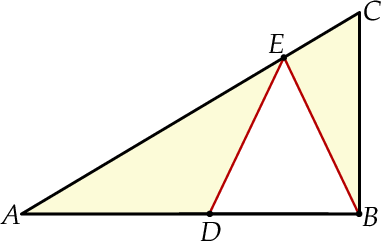
Oblicz jaką długość powinna mieć podstawa 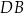 trójkąta
trójkąta 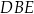 tak, aby jego pole było największe możliwe. Oblicz to największe pole.
tak, aby jego pole było największe możliwe. Oblicz to największe pole.
