Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, spełniające warunek: suma długości dłuższej podstawy  i wysokości trapezu jest równa 2.
i wysokości trapezu jest równa 2.
- Wyznacz wszystkie wartości
 , dla których istnieje trapez o podanych własnościach.
, dla których istnieje trapez o podanych własnościach. - Wykaż, że obwód
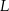 takiego trapezu, jako funkcja długości
takiego trapezu, jako funkcja długości  dłuższej podstawy trapezu, wyraża się wzorem
dłuższej podstawy trapezu, wyraża się wzorem 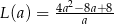
- Oblicz tangens kąta ostrego tego spośród rozpatrywanych trapezów, którego obwód jest najmniejszy.

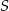 , aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
, aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej. 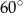 . Oblicz najmniejszą możliwą wartość obwodu trójkąta.
. Oblicz najmniejszą możliwą wartość obwodu trójkąta. 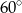 . Jaką najmniejszą wartość ma obwód tego trójkąta.
. Jaką najmniejszą wartość ma obwód tego trójkąta.  i
i 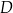 znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami
znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami  i
i  , a drugi węzeł z miastami
, a drugi węzeł z miastami  i
i  (zobacz rysunek).
(zobacz rysunek). 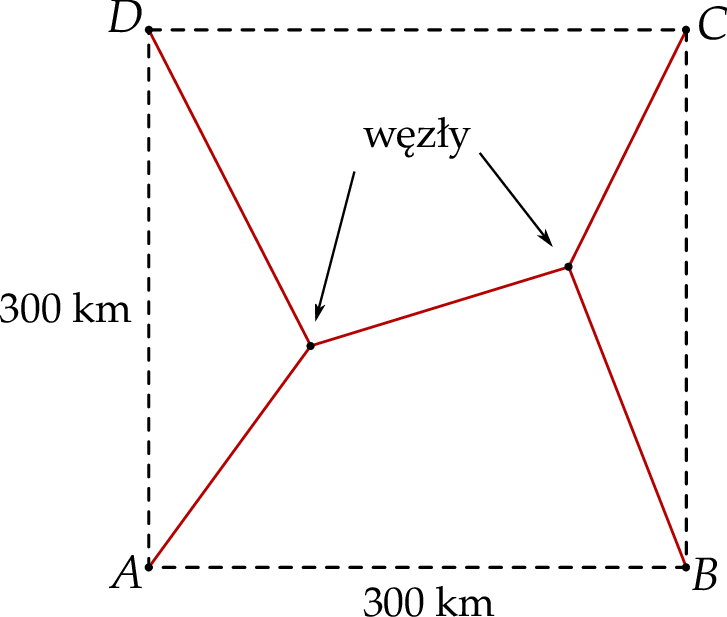
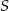 .
. 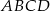 o wymiarach
o wymiarach 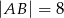 i
i 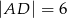 wybrano dwa punkty
wybrano dwa punkty 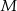 i
i 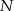 takie, że
takie, że 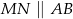 oraz
oraz 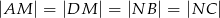 . Przy jakiej odległości punktów
. Przy jakiej odległości punktów 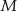 i
i 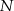 suma kwadratów długości odcinków
suma kwadratów długości odcinków 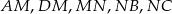 jest najmniejsza?
jest najmniejsza? 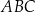 ma miarę mniejszą od
ma miarę mniejszą od 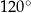 . Wyznacz taki punkt
. Wyznacz taki punkt 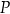 wewnątrz trójkąta
wewnątrz trójkąta 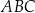 , dla którego suma
, dla którego suma 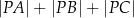 jest najmniejsza możliwa.
jest najmniejsza możliwa. 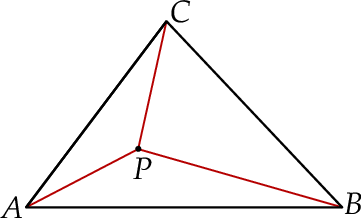
 ) do brzegu rzeki (prosta
) do brzegu rzeki (prosta  ) aby nabrać wodę (w punkcie
) aby nabrać wodę (w punkcie  ) i podlać rośliny w sadzie (punkt
) i podlać rośliny w sadzie (punkt  ).
). 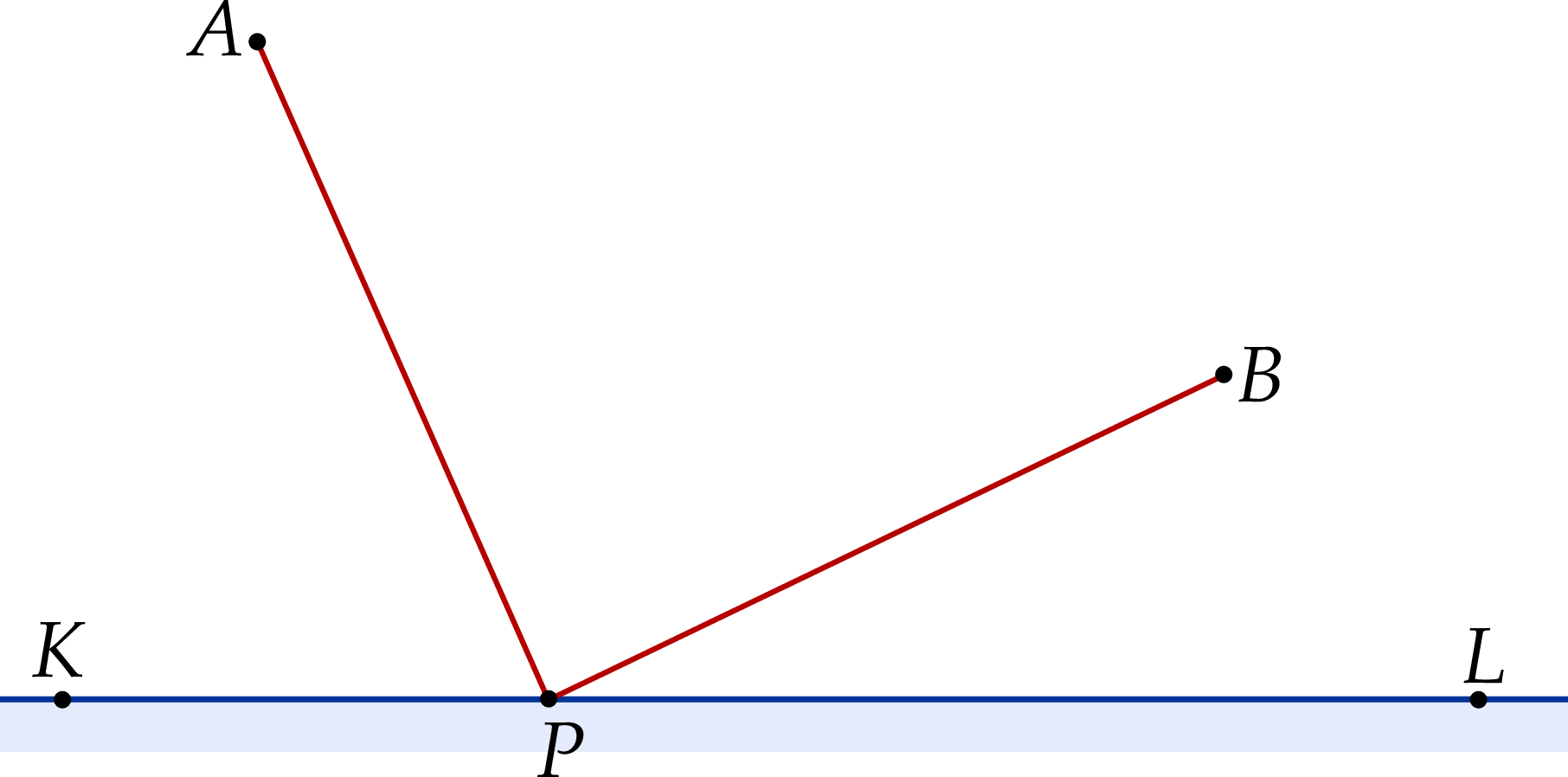
 , żeby pokonana przez niego droga (wzdłuż łamanej
, żeby pokonana przez niego droga (wzdłuż łamanej  ) była najkrótsza?
) była najkrótsza? 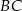 trójkąta
trójkąta 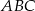 jeżeli
jeżeli 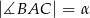 i pole trójkąta
i pole trójkąta 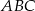 jest równe
jest równe 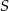 .
. 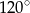 . Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.
. Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta. 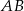 prostokąta
prostokąta 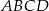 zawiera się w przeciwprostokątnej tego trójkąta, zaś punkty
zawiera się w przeciwprostokątnej tego trójkąta, zaś punkty 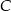 i
i 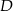 należą do przyprostokątnych. Oblicz długości boków prostokąta
należą do przyprostokątnych. Oblicz długości boków prostokąta 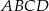 wiedząc, że kwadrat długości jego przekątnej
wiedząc, że kwadrat długości jego przekątnej 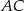 ma wartość najmniejszą z możliwych.
ma wartość najmniejszą z możliwych. 