Długości boków prostokąta 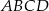 spełniają warunki:
spełniają warunki: 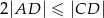 i
i 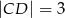 . Na boku
. Na boku 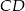 wybrano punkty
wybrano punkty 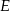 i
i 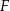 w ten sposób, że
w ten sposób, że 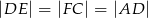 . Punkt
. Punkt 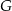 jest takim punktem odcinka
jest takim punktem odcinka 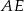 , że
, że 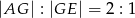 . Oblicz długość boku
. Oblicz długość boku 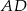 prostokąta, dla której pole trójkąta
prostokąta, dla której pole trójkąta 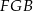 jest największe.
jest największe.
/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Największe pole
Dany jest romb 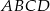 o boku długości 1, w którym kąt
o boku długości 1, w którym kąt 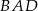 jest ostry i
jest ostry i 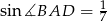 . Na bokach
. Na bokach 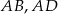 i
i 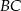 wybrano odpowiednio punkty
wybrano odpowiednio punkty 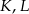 i
i 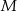 w ten sposób, że odcinki
w ten sposób, że odcinki 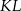 i
i 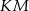 są równoległe do przekątnych rombu.
są równoległe do przekątnych rombu.
- Oblicz pole czworokąta
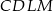 .
. - Oblicz największą możliwą wartość pola trójkąta
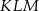 .
.
Rozpatrujemy wszystkie czworokąty 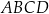 , które są jednoczenie wpisane w okrąg i opisane na okręgu, w których
, które są jednoczenie wpisane w okrąg i opisane na okręgu, w których 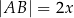 ,
, 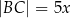 , i których obwód jest równy 10.
, i których obwód jest równy 10.
Pole czworokąta 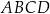 wpisanego w okrąg można obliczyć ze wzoru Brahmagupty
wpisanego w okrąg można obliczyć ze wzoru Brahmagupty
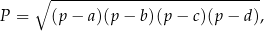
gdzie 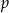 – jest połową obwodu czworokąta.
– jest połową obwodu czworokąta.
Zapisz pole czworokąta 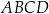 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych czworokątów, którego pole jest największe.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych czworokątów, którego pole jest największe.
Rozpatrujemy wszystkie trapezy równoramienne, w których każda z przekątnych ma długość 10. Niech  oznacza długość odcinka łączącego środki ramion trapezu.
oznacza długość odcinka łączącego środki ramion trapezu.
-
Wykaż, że pole
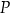 trapezu jako funkcja długości
trapezu jako funkcja długości  odcinka łączącego środki ramion trapezu jest określone wzorem
odcinka łączącego środki ramion trapezu jest określone wzorem 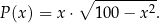
-
Wyznacz dziedzinę funkcji
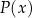 .
. -
Oblicz długość
 odcinka łączącego środki ramion tego z rozpatrywanych trapezów, którego pole jest największe. Oblicz to największe pole.
odcinka łączącego środki ramion tego z rozpatrywanych trapezów, którego pole jest największe. Oblicz to największe pole.
Rozpatrujemy wszystkie trójkąty równoramienne ostrokątne 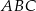 (
(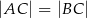 ), na których opisano okrąg o promieniu
), na których opisano okrąg o promieniu 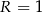 . Niech
. Niech  oznacza odległość środka okręgu od podstawy
oznacza odległość środka okręgu od podstawy 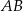 trójkąta.
trójkąta.
- Wykaż, że pole
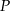 każdego z tych trójkątów, jako funkcja długości
każdego z tych trójkątów, jako funkcja długości  , wyraża się wzorem
, wyraża się wzorem 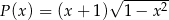 .
. - Wyznacz dziedzinę funkcji
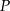 .
. - Oblicz długość odcinka
 tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
Rozpatrujemy wszystkie trójkąty równoramienne 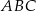 (
(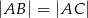 ), na których opisano okrąg o promieniu
), na których opisano okrąg o promieniu 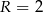 . Niech
. Niech 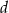 oznacza długość ramienia
oznacza długość ramienia 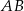 trójkąta.
trójkąta.
- Wykaż, że pole
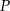 każdego z tych trójkątów, jako funkcja długości
każdego z tych trójkątów, jako funkcja długości 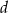 , wyraża się wzorem
, wyraża się wzorem 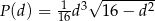 .
. - Wyznacz dziedzinę funkcji
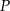 .
. - Oblicz długość ramienia
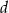 tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
Rozważamy wszystkie równoległoboki o obwodzie równym 200 i kącie ostrym o mierze 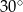 .
.
- Podaj wzór i dziedzinę funkcji opisującej zależność pola takiego równoległoboku od długości
 boku równoległoboku.
boku równoległoboku. - Oblicz wymiary tego z rozważanych równoległoboków, który ma największe pole, i oblicz to największe pole.
Rozważamy wszystkie równoległoboki o obwodzie równym 160 i kącie rozwartym o mierze 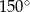 .
.
- Podaj wzór i dziedzinę funkcji opisującej zależność pola takiego równoległoboku od długości
 boku równoległoboku.
boku równoległoboku. - Oblicz wymiary tego z rozważanych równoległoboków, który ma największe pole, i oblicz to największe pole.
Ratownicy mający do dyspozycji linę o długości 80 metrów mają wytyczyć przy brzegu plaży kąpielisko w kształcie prostokąta (wzdłuż brzegu nie będzie liny). Jakie wymiary powinno mieć to kąpielisko, jeżeli wczasowicze chcą, aby miało ono jak największą powierzchnię? Należy przyjąć, że brzeg plaży tworzy linię prostą.
Zgodnie z założeniem architekta okno na poddaszu ma mieć kształt trapezu równoramiennego, który nie jest równoległobokiem. Dłuższa podstawa trapezu ma mieć długość 12 dm, a suma długości krótszej podstawy i wysokości tego trapezu ma być równa 18 dm. Oblicz, jaką długość powinna mieć krótsza podstawa tego trapezu, tak aby pole powierzchni okna było największe. Oblicz to pole.
Zgodnie z założeniem architekta okno na poddaszu ma mieć kształt trapezu równoramiennego, który nie jest równoległobokiem. Dłuższa podstawa trapezu ma mieć długość 16 dm, a suma długości krótszej podstawy i wysokości tego trapezu ma być równa 20 dm. Oblicz, jaką długość powinna mieć krótsza podstawa tego trapezu, tak aby pole powierzchni okna było największe. Oblicz to pole.
Z kawałka blachy należy wyciąć figurę w kształcie trapezu prostokątnego. Dłuższa podstawa trapezu ma mieć długość 6 dm, a suma długości krótszej podstawy i wysokości tego trapezu ma być równa 16 dm. Oblicz, jaką długość powinna mieć krótsza podstawa tego trapezu, tak aby pole powierzchni figury było największe. Oblicz to pole.
Działka ma kształt trójkąta o podstawie 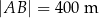 . Wysokość trójkąta opuszczona na podstawę
. Wysokość trójkąta opuszczona na podstawę 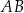 jest równa 125 m, a jego kąty
jest równa 125 m, a jego kąty 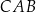 i
i 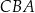 są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie
są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie 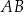 tego trójkąta, a dwa pozostałe –
tego trójkąta, a dwa pozostałe – 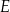 oraz
oraz 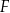 – na bokach
– na bokach 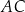 i
i 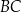 trójkąta (zobacz rysunek).
trójkąta (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię.
Obwód okna przedstawionego na rysunku wynosi 7 m. W jakim stosunku powinny pozostawać odcinki  i
i 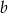 , aby przez okno wpadało jak najwięcej światła?
, aby przez okno wpadało jak najwięcej światła?
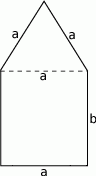
Dany jest trójkąt, w którym suma długości boku i wysokości opuszczonej na ten bok jest równa 8. Funkcja 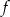 przyporządkowuje długości tego boku – pole trójkąta. Wyznacz wzór tej funkcji, jej dziedzinę, największą wartość, oraz zbiór wartości funkcji.
przyporządkowuje długości tego boku – pole trójkąta. Wyznacz wzór tej funkcji, jej dziedzinę, największą wartość, oraz zbiór wartości funkcji.

