Wyznacz wymiary prostokąta o obwodzie 36 cm, którego pole jest największe.
/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Największe pole
Z drutu o długości 320 cm zbudowano ramkę w kształcie prostokąta. Jakie powinna mieć wymiary aby pole prostokąta było największe?
Z drutu o długości 200 cm zbudowano ramkę w kształcie prostokąta. Jakie powinna mieć wymiary aby pole prostokąta było największe?
Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego przekątna ma długość 6 dm. Oblicz, jakie jest największe możliwe pole powierzchni tego okna.
Rozpatrujemy trapezy równoramienne  o przekątnej długości 1 i sumie długości podstaw równej
o przekątnej długości 1 i sumie długości podstaw równej  . Zapisz pole trapezu
. Zapisz pole trapezu  jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.
- Wykaż, że dla dowolnych liczb nieujemnych
 i
i  spełniona jest nierówność
spełniona jest nierówność 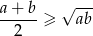
- W zbiorze prostokątów wpisanych w okrąg o promieniu
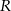 znajdź prostokąt o największym polu.
znajdź prostokąt o największym polu.
Dany jest okrąg o środku 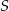 i promieniu 18. Rozpatrujemy pary okręgów: jeden o środku
i promieniu 18. Rozpatrujemy pary okręgów: jeden o środku 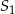 i promieniu
i promieniu  oraz drugi o środku
oraz drugi o środku 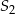 i promieniu
i promieniu 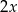 , o których wiadomo, że spełniają jednocześnie następujące warunki:
, o których wiadomo, że spełniają jednocześnie następujące warunki:
– rozważane dwa okręgi są styczne zewnętrznie;
– obydwa rozważane okręgi są styczne wewnętrznie do okręgu o środku 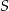 i promieniu 18;
i promieniu 18;
– punkty: 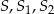 nie leżą na jednej prostej.
nie leżą na jednej prostej.
Pole trójkąta o bokach 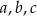 można obliczyć ze wzoru Herona
można obliczyć ze wzoru Herona
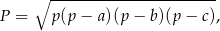
gdzie 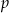 – jest połową obwodu trójkąta.
– jest połową obwodu trójkąta.
Zapisz pole trójkąta 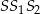 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
Dany jest okrąg o środku 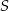 i promieniu 12. Rozpatrujemy pary okręgów: jeden o środku
i promieniu 12. Rozpatrujemy pary okręgów: jeden o środku 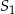 i promieniu
i promieniu  oraz drugi o środku
oraz drugi o środku 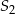 i promieniu
i promieniu 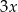 , o których wiadomo, że spełniają jednocześnie następujące warunki:
, o których wiadomo, że spełniają jednocześnie następujące warunki:
– rozważane dwa okręgi są styczne zewnętrznie;
– obydwa rozważane okręgi są styczne wewnętrznie do okręgu o środku 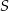 i promieniu 12;
i promieniu 12;
– punkty: 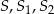 nie leżą na jednej prostej.
nie leżą na jednej prostej.
Zapisz pole trójkąta 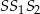 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
Rozważamy wszystkie trapezy równoramienne o obwodzie równym 96 i kącie ostrym o mierze 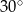 .
.
- Podaj wzór funkcji opisującej zależność pola takiego trapezu od długości
 jego ramienia.
jego ramienia. - Oblicz wymiary tego z rozważanych trapezów, który ma największe pole, i oblicz to największe pole.
W trójkąt prostokątny o przyprostokątnych długości 6 i 8 wpisujemy prostokąt w taki sposób, że dwa jego boki zawarte są w przyprostokątnych, a jeden z jego wierzchołków leży na przeciwprostokątnej. Zbadaj, jakie powinny być wymiary prostokąta, aby jego pole było możliwie największe.
Z odcinka drutu o długości 4 m wykonano ramkę w kształcie rombu z jedną przekątną (zobacz rysunek).
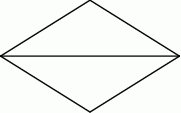
Jaka powinna być długość tej przekątnej, aby pole powierzchni tego rombu było największe możliwe?
Suma długości dwóch sąsiednich boków w pewnym trójkącie jest równa 14, a kąt między tymi bokami ma miarę 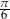 . Wyznacz długości boków trójkąta tak, aby jego pole było największe. Oblicz pole tego trójkąta.
. Wyznacz długości boków trójkąta tak, aby jego pole było największe. Oblicz pole tego trójkąta.
W trójkąt prostokątny o kącie ostrym 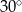 i przeciwprostokątnej długości 40 cm wpisujemy prostokąty w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w przeciwprostokątnej trójkąta. Zbadaj który z tych prostokątów ma największe pole.
i przeciwprostokątnej długości 40 cm wpisujemy prostokąty w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w przeciwprostokątnej trójkąta. Zbadaj który z tych prostokątów ma największe pole.
Arkusz blachy ma kształt trójkąta prostokątnego 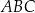 , w którym
, w którym 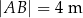 i
i 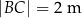 . Z tego arkusza należy wyciąć trójkąt równoramienny
. Z tego arkusza należy wyciąć trójkąt równoramienny 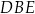 w ten sposób, że punkty
w ten sposób, że punkty 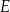 i
i 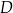 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 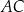 i
i 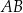 oraz
oraz 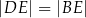 (zobacz rysunek).
(zobacz rysunek).
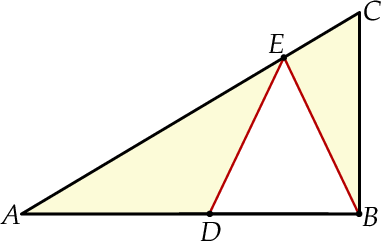
Oblicz jaką długość powinna mieć podstawa 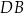 trójkąta
trójkąta 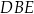 tak, aby jego pole było największe możliwe. Oblicz to największe pole.
tak, aby jego pole było największe możliwe. Oblicz to największe pole.
Obwód trapezu równoramiennego kącie ostrym 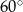 równa się
równa się 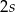 (
(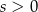 ). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole.
). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole.
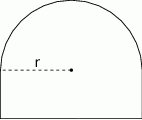
Z arkusza blachy w kształcie półkola o promieniu 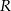 należy wyciąć trapez, którego jedna podstawa jest średnicą tego półkola, a wierzchołki drugiej podstawy leżą na jego brzegu (zobacz rysunek).
należy wyciąć trapez, którego jedna podstawa jest średnicą tego półkola, a wierzchołki drugiej podstawy leżą na jego brzegu (zobacz rysunek).
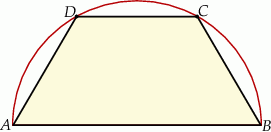
Oblicz jaką długość powinno mieć ramię tego trapezu, aby jego pole było największe możliwe. Oblicz to pole.
W kwadracie 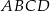 o boku długości 1 na boku
o boku długości 1 na boku 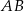 wybrano punkt
wybrano punkt 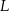 . Na bokach
. Na bokach 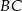 i
i 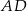 wybrano odpowiednio punkty
wybrano odpowiednio punkty 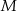 i
i 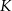 tak, że
tak, że 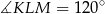 , a dwusieczna tego kąta jest równoległa do boku
, a dwusieczna tego kąta jest równoległa do boku 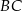 . Oblicz długości odcinków
. Oblicz długości odcinków 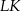 i
i 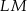 , dla których pole trójkąta
, dla których pole trójkąta 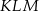 jest największe.
jest największe.
Rozpatrujemy wszystkie trójkąty równoramienne o obwodzie równym 18.
- Wykaż, że pole
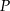 każdego z tych trójkątów, jako funkcja długości
każdego z tych trójkątów, jako funkcja długości 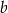 ramienia, wyraża się wzorem
ramienia, wyraża się wzorem 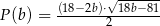 .
. - Wyznacz dziedzinę funkcji
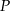 .
. - Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole.
Działka ma kształt trapezu. Podstawy 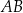 i
i 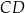 tego trapezu mają długości
tego trapezu mają długości 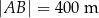 oraz
oraz 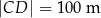 . Wysokość trapezu jest równa 75 m, a jego kąty
. Wysokość trapezu jest równa 75 m, a jego kąty 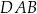 i
i 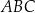 są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie
są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie 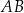 tego trapezu, a dwa pozostałe –
tego trapezu, a dwa pozostałe – 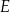 oraz
oraz 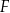 – na ramionach
– na ramionach 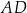 i
i 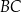 trapezu (zobacz rysunek).
trapezu (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię.
Działka ma kształt trapezu. Podstawy 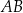 i
i 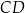 tego trapezu mają długości
tego trapezu mają długości 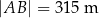 oraz
oraz 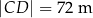 . Wysokość trapezu jest równa 54 m, a jego kąty
. Wysokość trapezu jest równa 54 m, a jego kąty 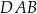 i
i 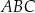 są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie
są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie 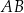 tego trapezu, a dwa pozostałe –
tego trapezu, a dwa pozostałe – 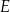 oraz
oraz 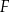 – na ramionach
– na ramionach 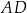 i
i 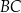 trapezu (zobacz rysunek).
trapezu (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię.
Budżet przeznaczony na ogrodzenie pewnej działki w kształcie trójkąta równoramiennego 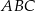 (
(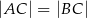 ) wynosi 12 000 zł.
) wynosi 12 000 zł.
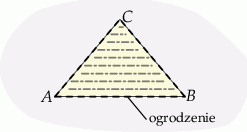
Ze względu na warunki terenowe, koszt wykonania 1 metra bieżącego ogrodzenia jest różny dla każdego z boków trójkąta 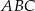 i wynosi odpowiednio: 140 zł dla boku
i wynosi odpowiednio: 140 zł dla boku 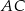 , 100 zł dla boku
, 100 zł dla boku 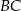 i 360 zł dla boku
i 360 zł dla boku 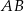 . Oblicz jakie powinny być wymiary ogrodzenia, aby odgradzało ono działkę o największym możliwym polu powierzchni. Wymiary podaj z dokładnością do 1 metra.
. Oblicz jakie powinny być wymiary ogrodzenia, aby odgradzało ono działkę o największym możliwym polu powierzchni. Wymiary podaj z dokładnością do 1 metra.
Rozpatrujemy wszystkie trójkąty prostokątne 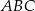 o przeciwprostokątnej
o przeciwprostokątnej 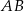 i obwodzie równym 4. Niech
i obwodzie równym 4. Niech 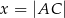 .
.
- Wykaż, że pole
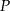 trójkąta
trójkąta 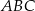 jako funkcja zmiennej
jako funkcja zmiennej  jest określone wzorem
jest określone wzorem 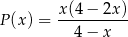
- Wyznacz dziedzinę funkcji
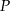 .
. - Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
Rozpatrujemy wszystkie prostokąty 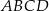 , w których suma długości dwóch sąsiednich boków i przekątnej jest równa 6. Niech
, w których suma długości dwóch sąsiednich boków i przekątnej jest równa 6. Niech 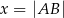 .
.
- Wykaż, że pole
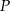 prostokąta
prostokąta 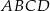 jako funkcja zmiennej
jako funkcja zmiennej  jest określone wzorem
jest określone wzorem 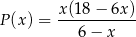
- Wyznacz dziedzinę funkcji
 .
. - Oblicz długości boków tego z rozpatrywanych prostokątów, który ma największe pole. Oblicz to największe pole.
W trójkąt prostokątny 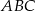 , w którym
, w którym  ,
, 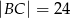 ,
, 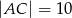 , wpisujemy prostokąty
, wpisujemy prostokąty 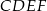 , tak, że punkt
, tak, że punkt  należy do boku
należy do boku 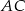 , pkt
, pkt 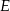 należy do boku
należy do boku 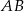 i punkt
i punkt 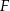 należy do boku
należy do boku 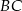 . Oblicz wymiary prostokąta o największym polu.
. Oblicz wymiary prostokąta o największym polu.
Przedstawiona na rysunku figura składa się z półkola i prostokąta. Oblicz maksymalne pole tej figury, jeżeli jej obwód jest równy 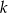 .
.
Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 4 dm. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby do pomieszczenia wpadało przez to okno jak najwięcej światła, czyli aby pole powierzchni okna było największe. Oblicz to pole.
Rozważamy zbiór wszystkich trapezów równoramiennych, których krótsza podstawa i ramiona mają długość 6. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby jego pole było największe. Oblicz to pole.
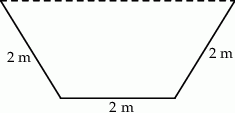
Betonowy kanał wodny ma mieć przekrój w kształcie trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 2 m. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby przez kanał mogło przepłynąć jak najwięcej wody, czyli aby pole powierzchni przekroju kanału było największe. Oblicz to pole przekroju.