Ciąg 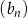 jest nieskończonym ciągiem liczb dodatnich, a ciąg
jest nieskończonym ciągiem liczb dodatnich, a ciąg 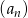 spełnia warunek
spełnia warunek
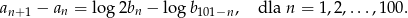
Oblicz 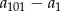 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 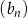 jest nieskończonym ciągiem liczb dodatnich, a ciąg
jest nieskończonym ciągiem liczb dodatnich, a ciąg 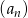 spełnia warunek
spełnia warunek
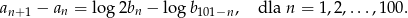
Oblicz 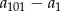 .
.
Ciąg 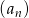 jest określony wzorem
jest określony wzorem 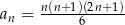 dla
dla 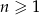 . Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
. Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
Suma 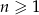 początkowych wyrazów ciągu
początkowych wyrazów ciągu 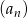 wyraża się wzorem
wyraża się wzorem 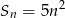 . Oblicz, ile wyrazów tego ciągu jest liczbami trzycyfrowymi.
. Oblicz, ile wyrazów tego ciągu jest liczbami trzycyfrowymi.
Wykazać, że 1 nie jest wyrazem ciągu 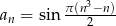 .
.
Ciąg 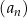 jest określony wzorem
jest określony wzorem
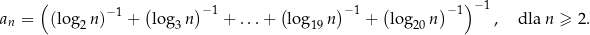
Oblicz sumę 19 początkowych wyrazów ciągu 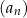 .
.
Udowodnij, że liczba 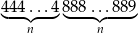 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Ciąg 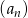 dany jest wzorem
dany jest wzorem 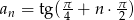 . Oblicz sumę
. Oblicz sumę 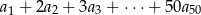 .
.
Dany jest ciąg 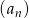 określony wzorem
określony wzorem 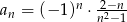 dla
dla 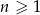 . Oblicz
. Oblicz 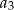 i
i 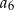 .
.
Niech 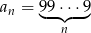 . Oblicz sumę 12 początkowych wyrazów ciągu
. Oblicz sumę 12 początkowych wyrazów ciągu 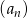 .
.
Niech 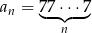 . Oblicz sumę 12 początkowych wyrazów ciągu
. Oblicz sumę 12 początkowych wyrazów ciągu 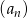 .
.
Nieskończony ciąg liczbowy 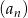 określony jest wzorem:
określony jest wzorem:
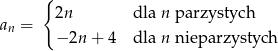
Ciąg 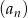 jest określony wzorem
jest określony wzorem 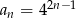 , gdzie
, gdzie 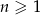 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 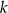 , dla których iloczyn
, dla których iloczyn 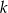 początkowych wyrazów ciągu
początkowych wyrazów ciągu 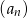 jest równy
jest równy 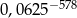 .
.
Różnica ciągu arytmetycznego 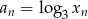 jest równa
jest równa 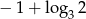 . Oblicz
. Oblicz 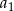 jeżeli wiadomo, że
jeżeli wiadomo, że
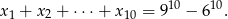
Ciąg 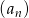 określony jest w taki sposób:
określony jest w taki sposób: 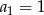 , zaś
, zaś  -ty wyraz ciągu
-ty wyraz ciągu 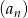 , gdy
, gdy 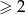 , jest największym dzielnikiem liczby
, jest największym dzielnikiem liczby  mniejszym od
mniejszym od  . Ile wyrazów ciągu
. Ile wyrazów ciągu 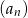 jest równych 2? Odpowiedź uzasadnij.
jest równych 2? Odpowiedź uzasadnij.
O ciągu 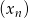 dla
dla 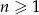 wiadomo, że:
wiadomo, że:
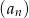 określony wzorem
określony wzorem 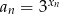 dla
dla 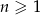 jest geometryczny o ilorazie
jest geometryczny o ilorazie 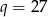 .
. 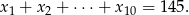
Oblicz 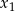 .
.
