Ciągi 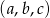 i
i 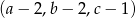 są ciągami geometrycznymi o wyrazach dodatnich, a ciąg
są ciągami geometrycznymi o wyrazach dodatnich, a ciąg 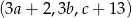 jest ciągiem arytmetycznym. Wyznacz
jest ciągiem arytmetycznym. Wyznacz 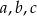 .
.
/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny
Trzy liczby tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy 8, to ciąg ten zmieni się w arytmetyczny. Jeżeli zaś do ostatniej liczby nowego ciągu arytmetycznego dodamy 64, to tak otrzymany ciąg będzie znów geometryczny. Znajdź te liczby. Uwzględnij wszystkie możliwości.
Pomiędzy liczby 243 i 48 wstaw takie trzy liczby, aby wraz z danymi tworzyły
- ciąg arytmetyczny;
- ciąg geometryczny.
Ciąg 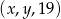 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 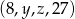 jest geometryczny. Oblicz
jest geometryczny. Oblicz 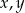 oraz
oraz  .
.
Trzy liczby całkowite tworzą ciąg geometryczny o ilorazie będącym ujemną liczbą całkowitą. Jeżeli najmniejszą z tych liczb zwiększymy o 9, to liczby te (w tej samej kolejności) są kolejnymi wyrazami ciągu arytmetycznego. Wyznacz te liczby.
Trzy różne liczby całkowite tworzą ciąg geometryczny o ilorazie będącym ujemną liczbą całkowitą. Jeżeli najmniejszą z tych liczb zwiększymy o 16, to liczby te (w tej samej kolejności) są kolejnymi wyrazami ciągu arytmetycznego. Wyznacz te liczby.
Ciąg 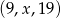 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 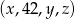 jest geometryczny. Oblicz
jest geometryczny. Oblicz 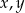 oraz
oraz  .
.
Ciąg 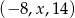 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 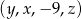 jest geometryczny. Oblicz
jest geometryczny. Oblicz 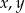 oraz
oraz  .
.
Wyznacz wzór na  -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
Rosnący ciąg arytmetyczny 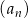 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 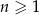 . Suma pierwszych dwunastu wyrazów tego ciągu jest równa 240. Wyrazy
. Suma pierwszych dwunastu wyrazów tego ciągu jest równa 240. Wyrazy 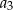 ,
, 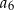 ,
, 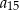 tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na
tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na  –ty wyraz ciągu arytmetycznego
–ty wyraz ciągu arytmetycznego  .
.
Wyznacz wzór na  -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 40, a wyrazy drugi, piąty i dwudziesty trzeci tworzą w podanej kolejności ciąg geometryczny.
-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 40, a wyrazy drugi, piąty i dwudziesty trzeci tworzą w podanej kolejności ciąg geometryczny.
Rosnący ciąg arytmetyczny 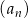 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 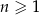 . Suma pierwszych pięciu wyrazów tego ciągu jest równa 10. Wyrazy
. Suma pierwszych pięciu wyrazów tego ciągu jest równa 10. Wyrazy 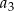 ,
, 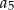 ,
, 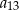 tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na
tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na  –ty wyraz ciągu arytmetycznego
–ty wyraz ciągu arytmetycznego 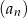 .
.
Liczby 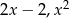 i
i 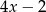 tworzą (w podanej kolejności) ciąg arytmetyczny i są trzema początkowymi wyrazami czterowyrazowego ciągu
tworzą (w podanej kolejności) ciąg arytmetyczny i są trzema początkowymi wyrazami czterowyrazowego ciągu 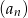 . Oblicz czwarty wyraz ciągu
. Oblicz czwarty wyraz ciągu 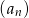 , wiedząc że liczby
, wiedząc że liczby 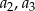 i
i 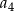 są trzema kolejnymi wyrazami pewnego ciągu geometrycznego.
są trzema kolejnymi wyrazami pewnego ciągu geometrycznego.
Dla jakich wartości  i
i 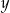 liczby
liczby 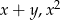 oraz
oraz 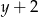 są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?
są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?
Dla jakich wartości  i
i 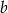 liczby
liczby 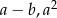 oraz
oraz 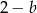 są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?
są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?
Wyznacz liczby  oraz
oraz 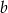 , dla których ciąg
, dla których ciąg 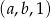 jest ciągiem arytmetycznym, natomiast ciąg
jest ciągiem arytmetycznym, natomiast ciąg 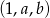 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
Ciąg 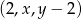 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 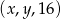 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 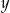 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny.
Ciąg 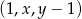 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 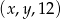 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 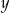 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny.
Wykaż, że jeżeli liczby 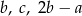 są kolejnymi wyrazami ciągu geometrycznego to liczby
są kolejnymi wyrazami ciągu geometrycznego to liczby 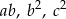 są kolejnymi wyrazami ciągu arytmetycznego.
są kolejnymi wyrazami ciągu arytmetycznego.
W nieskończonym ciągu arytmetycznym 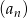 , określonym dla
, określonym dla 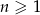 , suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy
, suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy 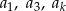 ciągu
ciągu 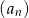 , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny
, w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 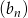 . Oblicz
. Oblicz 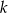 .
.
W nieskończonym ciągu arytmetycznym 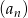 , określonym dla
, określonym dla 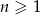 , suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy
, suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy 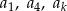 ciągu
ciągu 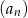 , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny
, w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 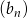 . Oblicz
. Oblicz 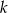 .
.
Pierwszy, trzeci i trzynasty wyraz ciągu arytmetycznego 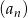 ,
, 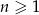 są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu
są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu 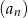 jest równy 27. Wyznacz wzór ciągu
jest równy 27. Wyznacz wzór ciągu 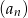 wiedząc, że nie jest to ciąg stały.
wiedząc, że nie jest to ciąg stały.
Dany jest nieskończony rosnący ciąg arytmetyczny 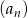 , dla
, dla 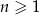 taki, że
taki, że 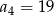 . Wyrazy
. Wyrazy 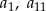 oraz
oraz 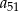 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 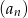 .
.
Dany jest nieskończony rosnący ciąg arytmetyczny 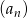 , dla
, dla 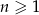 taki, że
taki, że 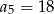 . Wyrazy
. Wyrazy 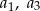 oraz
oraz 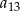 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 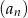 .
.
Pierwszy wyraz ciągu arytmetycznego 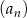 jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
- Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
- Dla jakiego
 liczby
liczby 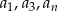 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?
Pierwszy wyraz ciągu arytmetycznego 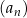 jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.
jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.
-
Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
-
Dla jakiego
 liczby
liczby 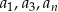 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?
Dany jest ciąg arytmetyczny 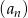 o różnicy
o różnicy 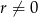 i pierwszym wyrazie
i pierwszym wyrazie 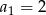 . Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
. Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.
Rosnące, trzywyrazowe ciągi arytmetyczny i geometryczny mają pierwsze wyrazy równe 9. Trzecie wyrazy tych ciągów są także równe. Drugi wyraz ciągu arytmetycznego jest o 2 większy od drugiego wyrazu ciągu geometrycznego. Wyznacz te ciągi.
Pierwszy, trzeci i jedenasty wyraz ciągu arytmetycznego o różnicy 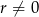 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 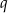 . Dla jakich wartości parametru
. Dla jakich wartości parametru 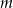 funkcja
funkcja 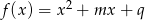 osiąga minimum większe od
osiąga minimum większe od 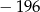 ?
?
Suma trzech początkowych wyrazów rosnącego ciągu geometrycznego 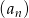 , określonego dla
, określonego dla 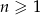 , jest równa
, jest równa 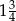 . Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego
. Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego 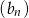 ,
, 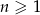 . Wyznacz wzór ciągu
. Wyznacz wzór ciągu 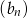 .
.

