Wyznacz wzór funkcji, której wykres powstaje z wykresu funkcji: 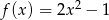 dla
dla  przez przesunięcie o wektor
przez przesunięcie o wektor ![→ u = [−1 ;2]](https://img.zadania.info/zad/7227565/HzadT2x.gif) .
.
/Szkoła średnia/Funkcje - wykresy/Parabola
Dana jest funkcja 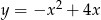 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→ u = [− 2,3]](https://img.zadania.info/zad/9470655/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Wykres funkcji 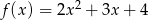 przesunięto o wektor
przesunięto o wektor ![→ v = [0,3]](https://img.zadania.info/zad/8939747/HzadT1x.gif) . Wyznacz wzór i narysuj wykres otrzymanej funkcji.
. Wyznacz wzór i narysuj wykres otrzymanej funkcji.
Funkcja 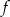 określona jest wzorem
określona jest wzorem 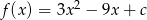 , gdzie
, gdzie 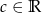 . Wyznacz wszystkie wartości współczynnika
. Wyznacz wszystkie wartości współczynnika  , dla których:
, dla których:
- jednym z miejsc zerowych funkcji
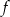 jest liczba 2;
jest liczba 2; - wierzchołek paraboli, która jest wykresem funkcji
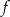 , należy do prostej o równaniu
, należy do prostej o równaniu 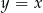 .
.
Wykresem funkcji 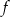 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 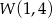 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 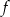 w przedziale
w przedziale 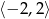 wynosi -5.
wynosi -5.
- Przedstaw wzór funkcji
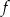 w postaci iloczynowej.
w postaci iloczynowej. - Rozwiąż nierówność
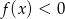 .
.
Dana jest funkcja 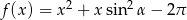 , dla
, dla 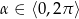 .
.
- Wyznacz wszystkie wartości parametru
 , dla których osią symetrii wykresu tej funkcji jest prosta
, dla których osią symetrii wykresu tej funkcji jest prosta 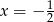 .
. - Wykaż, że nie istnieje taka wartość parametru
 , dla której do wykresu funkcji
, dla której do wykresu funkcji 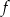 należy punkt
należy punkt 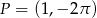 .
.
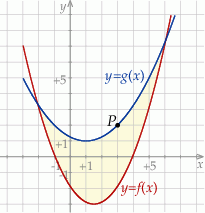
Naszkicuj 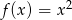 oraz
oraz 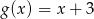 i na ich podstawie określ liczbę pierwiastków równania
i na ich podstawie określ liczbę pierwiastków równania 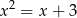 oraz znaki tych pierwiastków.
oraz znaki tych pierwiastków.
Do wykresu funkcji kwadratowej 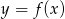 należą punkty
należą punkty 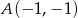 oraz
oraz 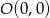 , który jest wierzchołkiem paraboli.
, który jest wierzchołkiem paraboli.
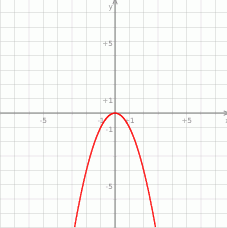
Wykres ten przesunięto w taki sposób, że otrzymano wykres funkcji 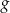 , której miejscami zerowymi są liczby 3 i 7.
, której miejscami zerowymi są liczby 3 i 7.
- Oblicz współrzędne wierzchołka paraboli będącej wykresem funkcji
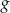 .
. - Narysuj wykres funkcji
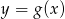 .
. - Rozwiąż nierówność
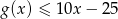 .
.
Dana jest funkcja kwadratowa 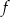 , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych
, której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych 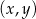 na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 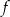 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
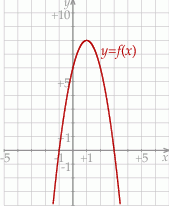
Rozwiąż nierówność 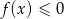 .
.
W kartezjańskim układzie współrzędnych  przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 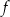 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji  , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
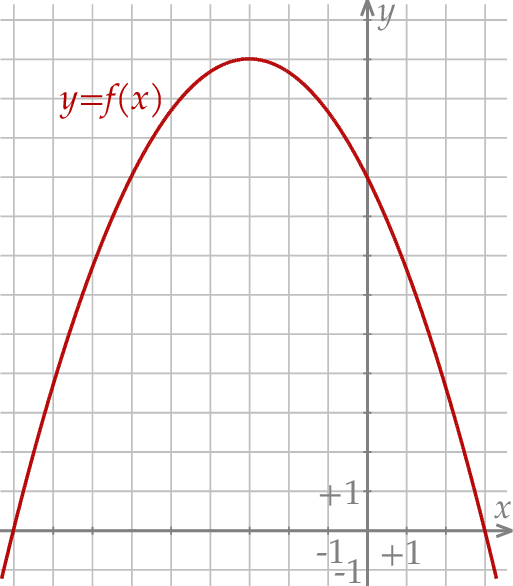
Wyznacz zbiór wszystkich argumentów, dla których funkcja 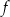 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
Dana jest funkcja kwadratowa 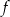 , której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 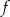 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
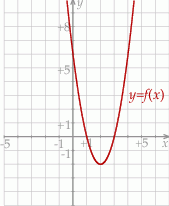
Rozwiąż nierówność 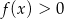 .
.
W kartezjańskim układzie współrzędnych  przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 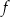 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
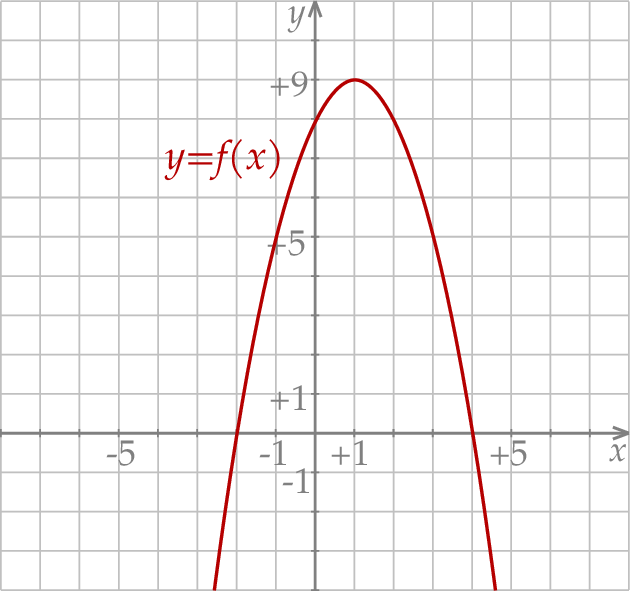
Rozwiąż nierówność  .
.
W kartezjańskim układzie współrzędnych  przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej  (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 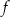 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
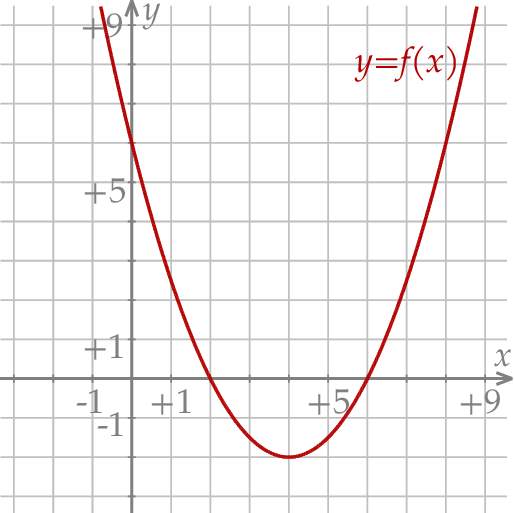
Zapisz poniżej w postaci przedziału zbiór wszystkich argumentów, dla których funkcja 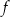 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych 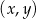 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 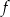 oraz
oraz 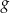 (zobacz rysunek).
(zobacz rysunek).
Funkcje 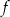 oraz
oraz 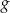 są określone wzorami
są określone wzorami 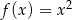 oraz
oraz 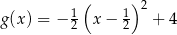 . Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt 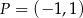 . Niech
. Niech 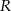 będzie punktem leżącym na wykresie funkcji
będzie punktem leżącym na wykresie funkcji 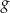 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 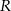 od punktu
od punktu 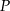 wyraża się wzorem
wyraża się wzorem
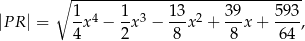
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 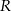 .
.
Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych 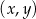 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 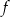 oraz
oraz 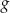 (zobacz rysunek).
(zobacz rysunek).
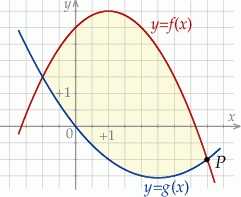
Funkcje 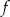 oraz
oraz 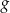 są określone wzorami
są określone wzorami 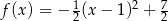 oraz
oraz  . Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt 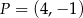 . Niech
. Niech 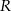 będzie punktem leżącym na wykresie funkcji
będzie punktem leżącym na wykresie funkcji 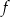 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 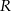 od punktu
od punktu 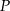 wyraża się wzorem
wyraża się wzorem
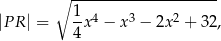
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 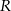 .
.
W parku krajobrazowym znajduje się zbiornik wodny, którego dwa brzegi postanowiono połączyć pomostem. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej zbiornika w kartezjańskim układzie współrzędnych 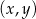 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 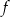 oraz
oraz 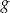 , które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
, które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
Funkcje 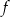 oraz
oraz 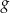 są określone wzorami
są określone wzorami 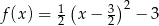 oraz
oraz 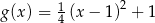 . Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją
. Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją 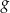 w punkcie o współrzędnych
w punkcie o współrzędnych 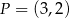 . Niech
. Niech 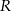 będzie punktem leżącym na wykresie
będzie punktem leżącym na wykresie 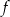 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 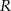 od punktu
od punktu 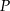 wyraża się wzorem
wyraża się wzorem
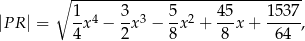
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 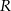 .
.
Wykresem funkcji kwadratowej 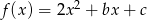 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 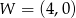 . Oblicz wartości współczynników
. Oblicz wartości współczynników 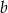 i
i  .
.
Wykresem funkcji kwadratowej 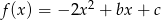 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 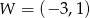 . Oblicz wartości współczynników
. Oblicz wartości współczynników 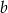 i
i  .
.
Funkcja kwadratowa 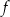 określona jest wzorem
określona jest wzorem 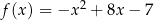 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  . Na paraboli
. Na paraboli 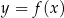 znajdź taki punkt
znajdź taki punkt 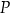 , który leży powyżej osi
, który leży powyżej osi 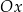 , i dla którego stosunek jego pierwszej współrzędnej do drugiej jest najmniejszy możliwy.
, i dla którego stosunek jego pierwszej współrzędnej do drugiej jest najmniejszy możliwy.
Funkcja kwadratowa 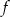 , której miejscami zerowymi są liczby
, której miejscami zerowymi są liczby 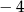 i 6, dla argumentu 1 przyjmuje wartość
i 6, dla argumentu 1 przyjmuje wartość 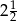 . Uzasadnij, że wykres funkcji
. Uzasadnij, że wykres funkcji 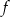 ma dwa punkty wspólne z prostą
ma dwa punkty wspólne z prostą 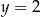 .
.
Funkcja kwadratowa 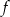 , której miejscami zerowymi są liczby
, której miejscami zerowymi są liczby 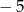 i 7, dla argumentu 1 przyjmuje wartość
i 7, dla argumentu 1 przyjmuje wartość 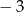 . Uzasadnij, że wykres funkcji
. Uzasadnij, że wykres funkcji 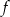 ma dwa punkty wspólne z prostą
ma dwa punkty wspólne z prostą 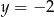 .
.
Wykresy funkcji kwadratowych 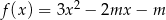 oraz
oraz 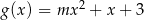 , dla
, dla 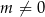 , przecinają się w dwóch punktach. Wyznacz wszystkie wartości
, przecinają się w dwóch punktach. Wyznacz wszystkie wartości 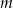 , dla których iloraz sumy odciętych tych punktów przez ich iloczyn jest o
, dla których iloraz sumy odciętych tych punktów przez ich iloczyn jest o  mniejszy od największej wartości funkcji
mniejszy od największej wartości funkcji 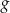 .
.
Wykres funkcji 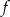 , określonej dla
, określonej dla 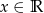 następującym wzorem
następującym wzorem
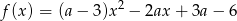
przecina dodatnią półoś 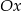 w dwóch różnych punktach.
w dwóch różnych punktach.
- Oblicz wartość wyrażenia
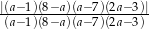 .
. - Uzasadnij, że dla każdych dwóch liczb rzeczywistych
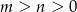 spełniona jest nierówność
spełniona jest nierówność 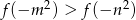 .
.
Funkcja kwadratowa 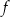 określona jest wzorem
określona jest wzorem 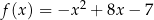 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  . Parabola będąca wykresem funkcji
. Parabola będąca wykresem funkcji 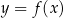 przecina prostą
przecina prostą 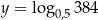 w punktach
w punktach 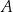 i
i 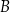 . Wykaż, że suma kwadratów pierwszych współrzędnych punktów
. Wykaż, że suma kwadratów pierwszych współrzędnych punktów 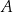 i
i 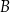 jest równa
jest równa 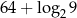 .
.
Dla jakich wartości parametru 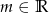 wierzchołek paraboli
wierzchołek paraboli 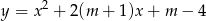 leży najbliżej prostej
leży najbliżej prostej 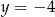 ?
?
Dla jakich wartości parametru 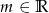 wierzchołek paraboli
wierzchołek paraboli 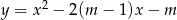 leży najbliżej osi
leży najbliżej osi 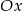 .
.
Na rysunku przedstawiono fragmenty wykresów funkcji kwadratowej oraz trzech funkcji liniowych. Zaznaczono również niektóre punkty szczególne tych wykresów: 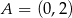 ,
, 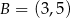 i
i 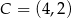 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 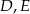 i
i 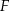 .
.
Dana jest funkcja kwadratowa określona wzorem 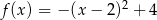 .
.
- podaj współrzędne wierzchołka paraboli będącej wykresem tej funkcji.
- podaj zbiór wartości tej funkcji.
- podaj równanie osi symetrii paraboli będącej wykresem tej funkcji.
- podaj wzór tej funkcji w postaci ogólnej.
Dana jest funkcja kwadratowa określona wzorem 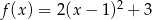 .
.
- podaj współrzędne wierzchołka paraboli będącej wykresem tej funkcji.
- podaj zbiór wartości tej funkcji.
- podaj równanie osi symetrii paraboli będącej wykresem tej funkcji.
- podaj wzór tej funkcji w postaci ogólnej.
Wyznacz współczynniki  i
i 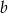 funkcji kwadratowej
funkcji kwadratowej 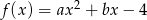 , jeśli współrzędne wierzchołka wynoszą
, jeśli współrzędne wierzchołka wynoszą 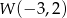 . Przedstaw trójmian w postaci iloczynowej.
. Przedstaw trójmian w postaci iloczynowej.
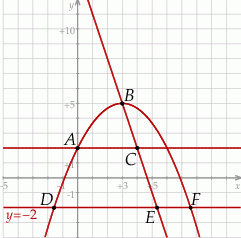
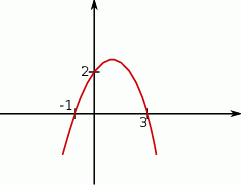
Na podstawie wykresu funkcji kwadratowej podaj jej wzór w postaci ogólnej, kanonicznej oraz iloczynowej.
Korzystając z wykresów funkcji 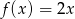 i
i 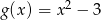 rozwiąż nierówność
rozwiąż nierówność 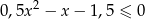 .
.

