Dla każdej liczby rzeczywistej 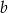 równanie
równanie 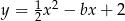 opisuje pewną parabolę. Wyznacz wszystkie wartości parametru
opisuje pewną parabolę. Wyznacz wszystkie wartości parametru 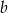 , dla których wierzchołek paraboli leży nad osią
, dla których wierzchołek paraboli leży nad osią 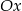 .
.
/Szkoła średnia/Funkcje - wykresy/Parabola
Wykres funkcji kwadratowej 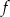 danej wzorem
danej wzorem 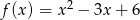 przecięto prostymi o równaniach
przecięto prostymi o równaniach 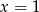 oraz
oraz 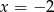 . Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji
. Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji  .
.
Wykres funkcji kwadratowej 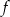 danej wzorem
danej wzorem 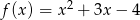 przecięto prostymi o równaniach
przecięto prostymi o równaniach 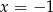 oraz
oraz 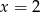 . Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji
. Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji 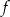 .
.
Wykres funkcji  przekształcono w symetrii względem prostej
przekształcono w symetrii względem prostej 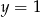 i otrzymano wykres funkcji
i otrzymano wykres funkcji 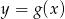 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 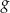 .
.
Wyznacz wszystkie funkcje kwadratowe, których wykres przechodzi przez punkty 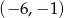 oraz
oraz 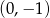 .
.
Punkty 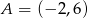 i
i 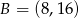 należą do wykresu funkcji
należą do wykresu funkcji 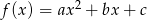 . Funkcja
. Funkcja 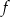 ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej
ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej 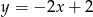 . Znajdź wzór tej funkcji.
. Znajdź wzór tej funkcji.
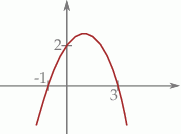
W kartezjańskim układzie współrzędnych 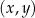 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 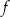 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 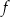 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
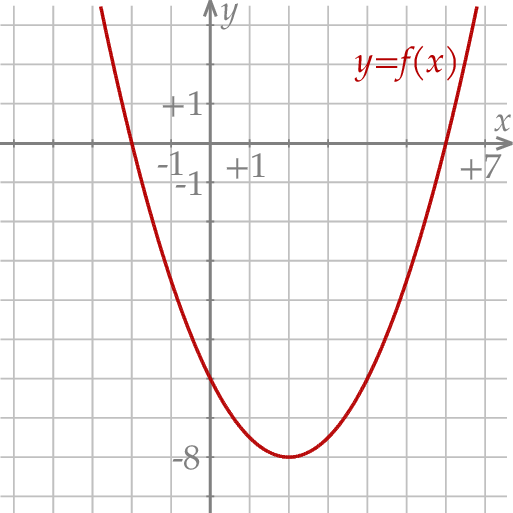
Wyznacz zbiór wszystkich argumentów, dla których funkcja 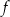 przyjmuje wartości z przedziału
przyjmuje wartości z przedziału ![[−6 ,0]](https://img.zadania.info/zad/1643883/HzadT5x.png) .
.
Na podstawie wykresu funkcji kwadratowej podaj jej wzór.
Na podstawie przedstawionego fragmentu wykresu funkcji kwadratowej wyznacz jej wzór.
Pole obszaru ograniczonego wykresem funkcji 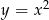 dla
dla 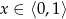 i osią
i osią 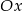 możemy obliczyć z dowolną dokładnością, zwiększając liczbę
możemy obliczyć z dowolną dokładnością, zwiększając liczbę  prostokątów o szerokości
prostokątów o szerokości 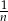 każdy (patrz rysunek) i sumując ich pola.
każdy (patrz rysunek) i sumując ich pola.
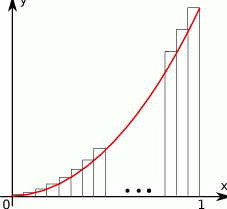
- Przedstaw ilustrację graficzną takiej sytuacji dla
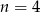 i oblicz sumę pól otrzymanych prostokątów.
i oblicz sumę pól otrzymanych prostokątów. 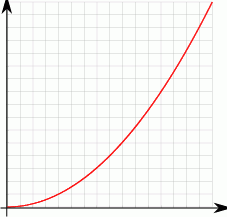
- Oblicz sumę
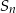 pól
pól  prostokątów, wykorzystując wzór:
prostokątów, wykorzystując wzór: 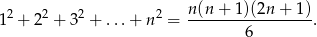
Wykres funkcji kwadratowej 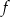 jest styczny do prostej
jest styczny do prostej 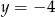 , przechodzi przez punkt
, przechodzi przez punkt 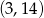 oraz jest symetryczny względem osi
oraz jest symetryczny względem osi 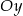 .
.
- Wyznacz wzór funkcji
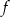 i narysuj jej wykres.
i narysuj jej wykres. - Rozwiąż nierówność
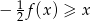
Dany jest wykres funkcji kwadratowej 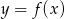
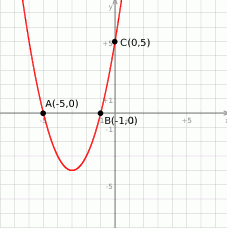
- Korzystając z danych na wykresie wyznacz wzór funkcji
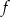 w postaci ogólnej.
w postaci ogólnej. - Oblicz współrzędne wierzchołka paraboli.
- Podaj zbiór rozwiązań nierówności
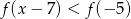 .
.
Napisz w postaci ogólnej, kanonicznej i iloczynowej wzór funkcji kwadratowej, jeśli do wykresu tej funkcji należy punkt 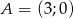 i funkcja osiąga wartość największą równą 12 dla argumentu 1.
i funkcja osiąga wartość największą równą 12 dla argumentu 1.
Funkcja kwadratowa, 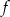 dla
dla 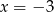 przyjmuje wartość największą równą 4. Do wykresu funkcji
przyjmuje wartość największą równą 4. Do wykresu funkcji 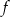 należy punkt
należy punkt 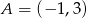 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 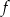 .
.
Funkcja kwadratowa 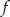 dla
dla 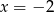 przyjmuje wartość największą równą 1. Do wykresu funkcji
przyjmuje wartość największą równą 1. Do wykresu funkcji 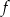 należy punkt
należy punkt 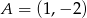 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 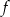 .
.
Funkcja 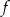 określona jest wzorem
określona jest wzorem 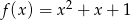 . Znajdź wzór funkcji
. Znajdź wzór funkcji 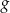 , której wykres otrzymamy:
, której wykres otrzymamy:
- przesuwając wykres funkcji o wektor
![[− 1;− 3]](https://img.zadania.info/zad/2335345/HzadT3x.gif) , a następnie otrzymany wykres przekształcając w symetrii względem osi
, a następnie otrzymany wykres przekształcając w symetrii względem osi 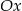 ;
; - dokonując obu przekształceń z poprzedniego punktu, ale w odwrotnej kolejności.
Dane są funkcje 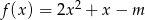 i
i 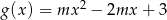 . Dla jakich wartości parametru
. Dla jakich wartości parametru 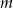 wykresy funkcji
wykresy funkcji 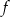 i
i 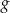 przecinają się w dwóch punktach, których odcięte mają różne znaki?
przecinają się w dwóch punktach, których odcięte mają różne znaki?
Punkty 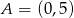 i
i 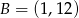 należą do wykresu funkcji
należą do wykresu funkcji 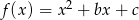 . Zapisz wzór funkcji w postaci ogólnej, kanonicznej i iloczynowej.
. Zapisz wzór funkcji w postaci ogólnej, kanonicznej i iloczynowej.
Naszkicuj wykres funkcji 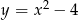 .
.
Naszkicuj wykres funkcji 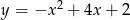 .
.
Naszkicuj wykres funkcji 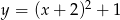 .
.
Naszkicuj wykres funkcji 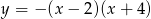 .
.
Naszkicuj wykres funkcji 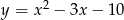 .
.
Naszkicuj wykres funkcji 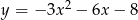 .
.
Dla jakiego 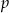 prosta o równaniu
prosta o równaniu 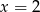 jest osią symetrii wykresu funkcji
jest osią symetrii wykresu funkcji 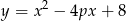 .
.
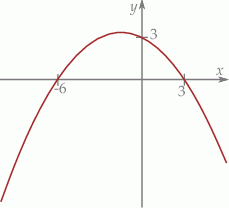
W kartezjańskim układzie współrzędnych 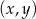 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 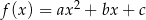 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 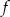 , ma współrzędne
, ma współrzędne 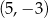 . Jeden z punktów przecięcia paraboli z osią
. Jeden z punktów przecięcia paraboli z osią 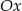 układu współrzędnych ma współrzędne
układu współrzędnych ma współrzędne 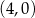 .
.
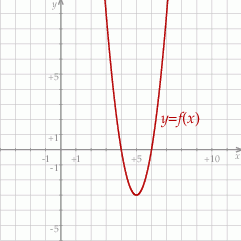
Wyznacz zbiór wszystkich wartości funkcji 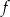 .
.
W kartezjańskim układzie współrzędnych 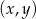 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 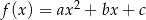 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 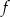 , ma współrzędne
, ma współrzędne  . Jeden z punktów przecięcia paraboli z osią
. Jeden z punktów przecięcia paraboli z osią 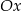 układu współrzędnych ma współrzędne
układu współrzędnych ma współrzędne 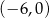 .
.
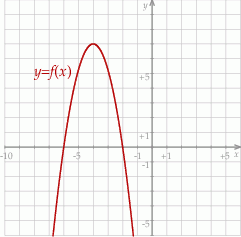
Wyznacz zbiór wszystkich wartości funkcji 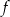 .
.
Dana jest funkcja 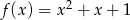 . Napisz wzór funkcji otrzymanej z
. Napisz wzór funkcji otrzymanej z 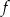 przez
przez
- symetrię względem osi
 ;
; - symetrię względem osi
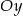 ;
; - symetrię względem punktu
 .
.
Wyznacz te wartości współczynnika  , dla których wierzchołek paraboli, będącej wykresem funkcji
, dla których wierzchołek paraboli, będącej wykresem funkcji 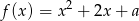 , należy do paraboli o równaniu
, należy do paraboli o równaniu 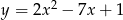 .
.
Dany jest trójmian kwadratowy 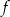 o współczynniku 3 przy najwyższej potędze
o współczynniku 3 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 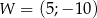 . Wyznacz
. Wyznacz 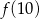 .
.
Dany jest trójmian kwadratowy 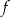 o współczynniku 4 przy najwyższej potędze
o współczynniku 4 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 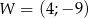 . Wyznacz
. Wyznacz 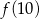 .
.

