Dana jest funkcja kwadratowa 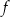 , której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji 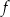 jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
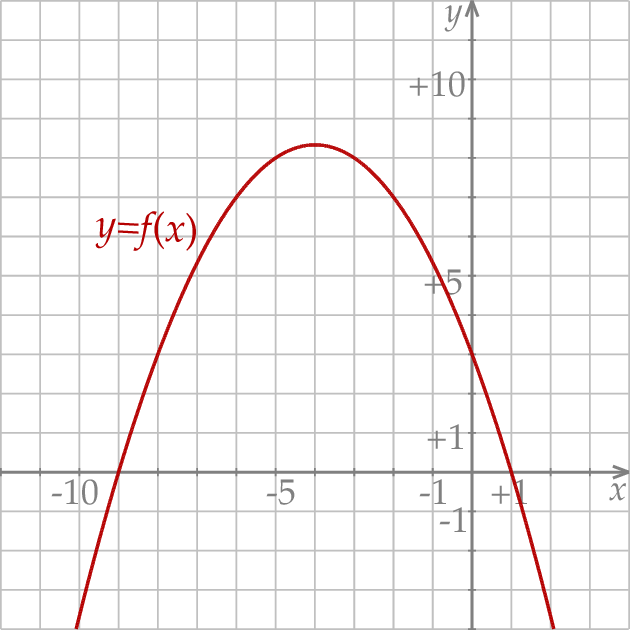
Wyznacz zbiór wartości funkcji 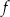 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dana jest funkcja kwadratowa 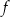 , której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji 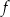 jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.

Wyznacz zbiór wartości funkcji 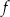 .
.
Na wykresie funkcji 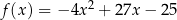 wyznacz taki punkt
wyznacz taki punkt 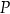 , którego druga współrzędna jest 7 razy większa od pierwszej współrzędnej.
, którego druga współrzędna jest 7 razy większa od pierwszej współrzędnej.
Dana jest funkcja kwadratowa 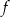 , której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji 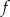 jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
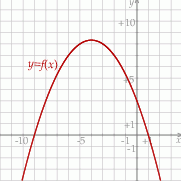
Rozwiąż nierówność 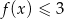 .
.
Wykresy funkcji kwadratowych 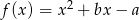 oraz
oraz 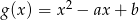 , gdzie
, gdzie 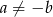 , przecinają się w punkcie leżącym na osi
, przecinają się w punkcie leżącym na osi 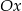 . Wiedząc, że osią symetrii wykresu funkcji
. Wiedząc, że osią symetrii wykresu funkcji 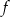 jest prosta o równaniu
jest prosta o równaniu 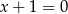 , oblicz
, oblicz 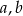 .
.
W kartezjańskim układzie współrzędnych 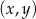 przedstawiono oś symetrii wykresu funkcji kwadratowej
przedstawiono oś symetrii wykresu funkcji kwadratowej 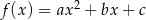 . Przedstawiono również prostą
. Przedstawiono również prostą 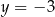 , z którą wykres funkcji
, z którą wykres funkcji 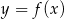 ma dokładnie jeden punkt wspólny, oraz jeden z punktów tego wykresu –
ma dokładnie jeden punkt wspólny, oraz jeden z punktów tego wykresu – 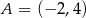
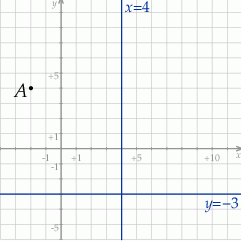
Wyznacz wzór funkcji kwadratowej 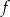 w postaci kanonicznej.
w postaci kanonicznej.
Wyznacz wszystkie wartości parametrów  i
i 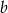 , dla których wykresy funkcji
, dla których wykresy funkcji
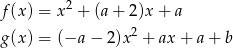
przecinają się w dwóch różnych punktach leżących na osi 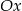 .
.
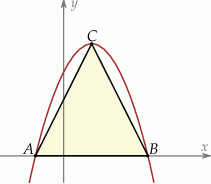
Wierzchołki trójkąta 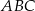 leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej
leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej 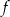 (zobacz rysunek). Pole tego trójkąta jest równe 8, punkt
(zobacz rysunek). Pole tego trójkąta jest równe 8, punkt 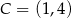 jest wierzchołkiem paraboli, a punkty
jest wierzchołkiem paraboli, a punkty 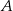 i
i 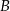 leżą na osi
leżą na osi 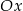 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 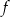 .
.
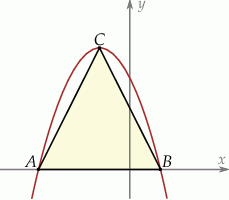
Wierzchołki trójkąta 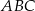 leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej
leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej 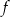 (zobacz rysunek). Pole tego trójkąta jest równe 8, punkt
(zobacz rysunek). Pole tego trójkąta jest równe 8, punkt 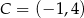 jest wierzchołkiem paraboli, a punkty
jest wierzchołkiem paraboli, a punkty 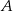 i
i 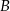 leżą na osi
leżą na osi 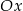 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 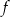 .
.
Znajdź wzór funkcji kwadratowej 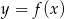 , której wykresem jest parabola o wierzchołku
, której wykresem jest parabola o wierzchołku 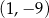 przechodząca przez punkt o współrzędnych
przechodząca przez punkt o współrzędnych 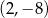 . Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
. Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
Napisz równanie osi symetrii wykresu funkcji 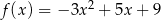 .
.
Wykresem funkcji kwadratowej 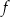 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 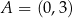 . Punkt
. Punkt 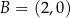 leży na wykresie funkcji
leży na wykresie funkcji 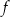 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 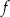 .
.
Wykres funkcji kwadratowej 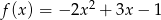 przesunięto o
przesunięto o 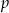 jednostek wzdłuż osi
jednostek wzdłuż osi 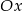 i o
i o 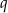 jednostek wzdłuż osi
jednostek wzdłuż osi 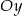 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 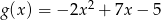 .
.
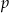 i
i 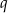 .
. 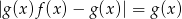 .
.Wykres funkcji 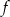 danej wzorem
danej wzorem 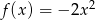 przesunięto wzdłuż osi
przesunięto wzdłuż osi 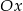 o 3 jednostki w prawo oraz wzdłuż osi
o 3 jednostki w prawo oraz wzdłuż osi 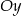 o 8 jednostek w górę, otrzymując wykres funkcji
o 8 jednostek w górę, otrzymując wykres funkcji 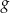 .
.
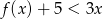 .
. 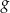 .
. 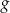 określona jest wzorem
określona jest wzorem 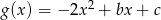 . Oblicz
. Oblicz 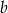 i
i  .
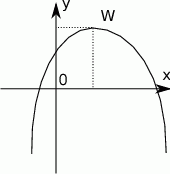
.Wykorzystując poniższy szkic wykresu funkcji kwadratowej o równaniu 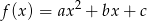 , gdzie
, gdzie 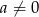 określ znak następujących wyrażeń:
określ znak następujących wyrażeń:

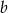

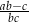
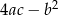
Prosta 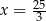 jest osią symetrii paraboli będącej wykresem funkcji kwadratowej
jest osią symetrii paraboli będącej wykresem funkcji kwadratowej 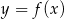 . Do wykresu tego należy punkt o współrzędnych
. Do wykresu tego należy punkt o współrzędnych 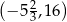 . Wyznacz wszystkie rozwiązania równania
. Wyznacz wszystkie rozwiązania równania 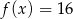 .
.
Dana jest funkcja kwadratowa 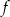 , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych
, której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych 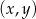 na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 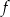 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
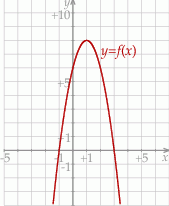
Wyznacz wzór funkcji kwadratowej 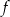 w postaci kanonicznej.
w postaci kanonicznej.
W kartezjańskim układzie współrzędnych 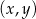 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 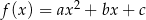 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 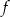 , ma współrzędne
, ma współrzędne 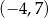 . Jeden z punktów przecięcia paraboli z osią
. Jeden z punktów przecięcia paraboli z osią 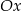 układu współrzędnych ma współrzędne
układu współrzędnych ma współrzędne 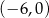 .
.
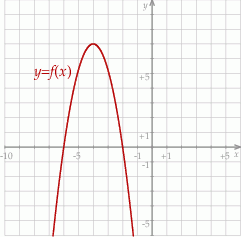
Wyznacz wzór funkcji kwadratowej 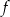 w postaci kanonicznej.
w postaci kanonicznej.
W kartezjańskim układzie współrzędnych 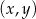 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 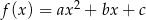 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 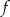 , ma współrzędne
, ma współrzędne 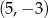 . Jeden z punktów przecięcia paraboli z osią
. Jeden z punktów przecięcia paraboli z osią 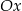 układu współrzędnych ma współrzędne
układu współrzędnych ma współrzędne 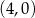 .
.
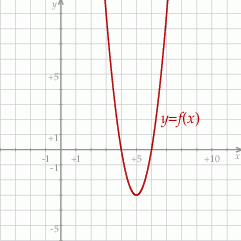
Wyznacz wzór funkcji kwadratowej 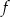 w postaci kanonicznej.
w postaci kanonicznej.
Dana jest funkcja kwadratowa 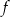 , której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 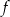 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
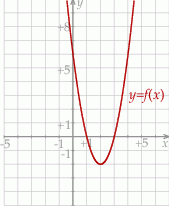
Wyznacz wzór funkcji kwadratowej 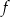 w postaci kanonicznej.
w postaci kanonicznej.
Dane są dwie funkcje kwadratowe 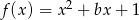 oraz
oraz 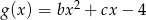 . Wyznacz wartości parametrów
. Wyznacz wartości parametrów 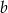 oraz
oraz  , tak aby wykresy funkcji miały wierzchołek w punkcie o odciętej -2.
, tak aby wykresy funkcji miały wierzchołek w punkcie o odciętej -2.
Napisz wzór funkcji kwadratowej w postaci ogólnej wiedząc, że funkcja ma jedno miejsce zerowe oraz do jej wykresu należą punkty 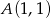 oraz
oraz 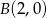 .
.
Parabola, która jest wykresem funkcji kwadratowej 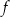 , ma z osiami kartezjańskiego układu współrzędnych
, ma z osiami kartezjańskiego układu współrzędnych 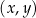 dokładnie dwa punkty wspólne:
dokładnie dwa punkty wspólne: 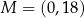 oraz
oraz 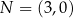 . Wyznacz wzór funkcji kwadratowej
. Wyznacz wzór funkcji kwadratowej 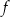 .
.
Pewna parabola o wierzchołku 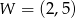 przecina oś
przecina oś 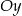 w punkcie
w punkcie 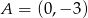 .
.
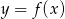 , której wykresem jest ta parabola.
, której wykresem jest ta parabola. 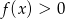 .
.Wykres funkcji kwadratowej 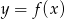 przesunięto o 2 jednostki do góry, następnie nowy wykres o 3 jednostki w lewo i otrzymano wykres funkcji
przesunięto o 2 jednostki do góry, następnie nowy wykres o 3 jednostki w lewo i otrzymano wykres funkcji 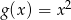 . Wyznacz wzór ogólny funkcji
. Wyznacz wzór ogólny funkcji 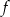 .
.
Wykres funkcji kwadratowej 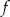 określonej wzorem
określonej wzorem 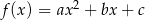 ma z prostą o równaniu
ma z prostą o równaniu 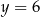 dokładnie jeden punkt wspólny. Punkty
dokładnie jeden punkt wspólny. Punkty 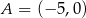 i
i 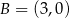 należą do wykresu funkcji
należą do wykresu funkcji 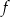 . Oblicz wartości współczynników
. Oblicz wartości współczynników 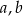 oraz
oraz  .
.
