Wyznacz cztery początkowe wyrazy ciągu geometrycznego, jeśli: 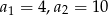 .
.
/Szkoła średnia/Ciągi/Geometryczny/Czterowyrazowy
Różnica między drugim wyrazem ciągu geometrycznego a pierwszym wyrazem tego ciągu wynosi -6, a różnica między czwartym a pierwszym wyrazem tego ciągu jest równa -18. Oblicz trzeci wyraz tego ciągu.
Liczby 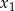 i
i 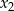 są różnymi od zera rozwiązaniami równania
są różnymi od zera rozwiązaniami równania 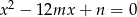 . Liczby
. Liczby 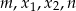 są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz
są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz 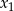 i
i 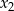 .
.
Liczby  i
i 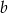 są pierwiastkami równania
są pierwiastkami równania 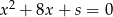 , a liczby
, a liczby  i
i 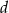 są pierwiastkami równania
są pierwiastkami równania 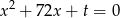 . Ciąg
. Ciąg 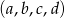 jest malejącym ciągiem geometrycznym. Oblicz
jest malejącym ciągiem geometrycznym. Oblicz  i
i 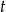 .
.
Dany jest czterowyrazowy ciąg 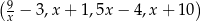 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 27, a iloczyn drugiej i trzeciej jest równy 72. Wyznacz te liczby.
Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 52, a iloczyn drugiej i trzeciej jest równy 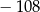 . Wyznacz te liczby.
. Wyznacz te liczby.
Liczby 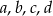 są czterema kolejnymi wyrazami ciągu geometrycznego. Trzecia liczba jest o 9 większa od pierwszej, a druga liczba jest o 18 większa od czwartej. Wyznacz te liczby.
są czterema kolejnymi wyrazami ciągu geometrycznego. Trzecia liczba jest o 9 większa od pierwszej, a druga liczba jest o 18 większa od czwartej. Wyznacz te liczby.
Podstawy czterech logarytmów liczby  tworzą ciąg geometryczny o ilorazie
tworzą ciąg geometryczny o ilorazie  . Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych
. Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych
Ciąg 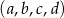 ma wszystkie wyrazy ujemne i jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 2. Oblicz iloczyn
ma wszystkie wyrazy ujemne i jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 2. Oblicz iloczyn 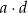 .
.
Liczbę 255 przedstaw jako sumę czterech całkowitych składników będących kolejnymi wyrazami ciągu geometrycznego tak, aby trzeci wyraz był o 45 większy od wyrazu pierwszego.
Cztery liczby tworzą ciąg geometryczny. Wyznacz te liczby wiedząc, że suma pierwszej i czwartej wynosi 36, a suma drugiej i trzeciej liczby wynosi 24.
Liczby 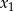 i
i 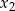 są pierwiastkami równania
są pierwiastkami równania 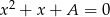 , a liczby
, a liczby 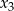 i
i 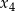 są pierwiastkami równania
są pierwiastkami równania 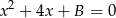 . Wiadomo, że ciąg
. Wiadomo, że ciąg 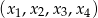 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 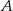 i
i 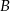 .
.

