Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Wyszukiwanie zadań

Uzasadnij, że równanie 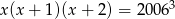3 x(x+ 1)(x + 2) = 20 06 nie ma pierwiastków całkowitych.

Rozwiązanie (2138828)

Wyznacz wszystkie liczby naturalne dodatnie 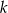k , dla których równanie 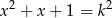x 2 + x + 1 = k2 ma pierwiastki będące liczbami całkowitymi.

Rozwiązanie (2521932)

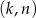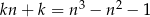Wyznacz wszystkie pary liczb całkowitych (k,n) spełniających równość kn + k = n3 − n2 − 1 .

Rozwiązanie (2943812)

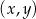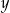Wyznacz wszystkie pary (x,y) , gdzie x i y są liczbami całkowitymi spełniającymi równanie

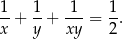
1-+ 1-+ 1--= 1. x y xy 2
Rozwiązanie (2981527)

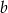Liczby naturalne a i b spełniają równość 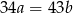34a = 43b . Udowodnij, że liczba 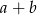a + b jest złożona.

Rozwiązanie (3038381)

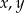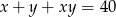Wyznacz wszystkie liczby całkowite x ,y spełniające równanie x + y + xy = 40 .

Rozwiązanie (3202710)

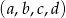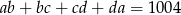Ile jest takich czwórek liczb całkowitych i dodatnich (a,b,c,d) , które spełniają równanie ab + bc + cd + da = 1004 .

Rozwiązanie (6261209)

Uzasadnij, że równanie 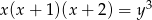3 x (x+ 1)(x + 2) = y nie ma rozwiązań w liczbach całkowitych dodatnich x,y .

Rozwiązanie (6296453)

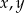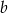Wykaż, że jeżeli liczby całkowite a i b spełniają równanie

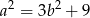
2 2 a = 3b + 9

to liczba 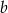b dzieli się przez 3, a liczba a nie dzieli się przez 9.

Rozwiązanie (6983037)

Wyznacz wszystkie pary liczb całkowitych dodatnich 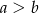a > b , dla których

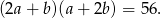
(2a+ b)(a+ 2b) = 56 .
Rozwiązanie (7853047)

Iloczyn trzech liczb pierwszych jest pięć razy większy od ich sumy. Wyznacz te liczby.

Rozwiązanie (8366833)

Wyznacz wszystkie liczby pierwsze 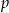p i liczby naturalne n spełniające równość

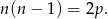
n(n − 1) = 2p .
Rozwiązanie (9147597)

Wykaż, że równanie 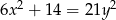2 2 6x + 14 = 21y nie ma rozwiązań całkowitych.

Rozwiązanie (9605119)