Ciąg 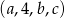 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 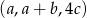 jest geometryczny. Oblicz
jest geometryczny. Oblicz 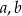 i
i  .
.
/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Czterowyrazowy
Między liczby 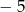 i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Między liczby 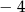 i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Czterowyrazowy ciąg 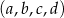 jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg
jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg 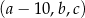 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 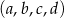 .
.
Czterowyrazowy ciąg 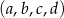 jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg
jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg 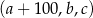 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 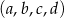 .
.
Czterowyrazowy ciąg 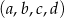 jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg
jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg 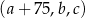 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 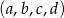 .
.
Cztery liczby tworzą ciąg geometryczny. Jeżeli od pierwszej z nich odejmiemy 2, od drugiej 3, od trzeciej 9, a od czwartej 25, to otrzymane różnice utworzą ciąg arytmetyczny. Znajdź te liczby.
Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 14, a suma drugiej i trzeciej wynosi 12. Wyznacz te 4 liczby.
Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 22, a suma drugiej i trzeciej wynosi 4. Wyznacz te 4 liczby.
Liczby 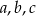 są kolejnymi wyrazami ciągu arytmetycznego, zaś liczby
są kolejnymi wyrazami ciągu arytmetycznego, zaś liczby 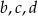 są kolejnymi wyrazami ciągu geometrycznego. Suma pierwszej trójki liczb wynosi 12, a drugiej 19. Wyznacz liczby
są kolejnymi wyrazami ciągu geometrycznego. Suma pierwszej trójki liczb wynosi 12, a drugiej 19. Wyznacz liczby 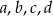 .
.
Ciąg 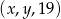 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 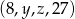 jest geometryczny. Oblicz
jest geometryczny. Oblicz 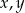 oraz
oraz  .
.
Ciąg 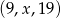 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 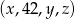 jest geometryczny. Oblicz
jest geometryczny. Oblicz 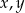 oraz
oraz  .
.
Ciąg 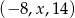 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 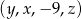 jest geometryczny. Oblicz
jest geometryczny. Oblicz 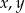 oraz
oraz  .
.
Liczby 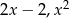 i
i 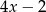 tworzą (w podanej kolejności) ciąg arytmetyczny i są trzema początkowymi wyrazami czterowyrazowego ciągu
tworzą (w podanej kolejności) ciąg arytmetyczny i są trzema początkowymi wyrazami czterowyrazowego ciągu 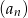 . Oblicz czwarty wyraz ciągu
. Oblicz czwarty wyraz ciągu 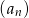 , wiedząc że liczby
, wiedząc że liczby 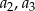 i
i 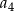 są trzema kolejnymi wyrazami pewnego ciągu geometrycznego.
są trzema kolejnymi wyrazami pewnego ciągu geometrycznego.

