Równania z pierwiastkami - zadania z matematyki

/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Znajdź takie wartości parametru 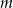, aby połowa jednego pierwiastka równania 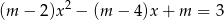(m − 2)x2 − (m − 4)x + m = 3 była równa odwrotności drugiego pierwiastka.

Dla jakich wartości parametru 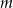jeden z pierwiastków równania 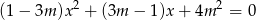(1 − 3m )x2 + (3m − 1)x + 4m 2 = 0 jest połową drugiego pierwiastka?

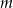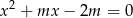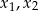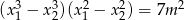Wyznacz wszystkie wartości parametru , dla których równanie x 2 + mx − 2m = 0 ma dwa różne rozwiązania rzeczywiste x1,x2 spełniające warunek (x31 − x32)(x21 − x22) = 7m 2 .

Dla jakich wartości parametru suma kwadratów różnych pierwiastków równania

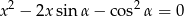
x 2 − 2x sinα − c os2α = 0

jest równa 3?

Ukryj Podobne zadania

Dla jakiego 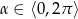α ∈ ⟨0,2 π⟩ pierwiastki równania

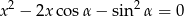
2 2 x − 2x cos α− sin α = 0

spełniają warunek 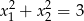2 2 x1 + x2 = 3 ?

Wyznacz wszystkie wartości parametru 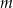, dla których równanie

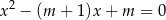
2 x − (m + 1)x + m = 0

ma dwa różne rozwiązania rzeczywiste 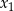x 1 oraz 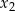, spełniające warunki:

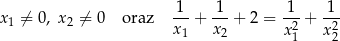
1 1 1 1 x 1 ⁄= 0, x2 ⁄= 0 oraz ---+ ---+ 2 = --+ --- x 1 x2 x21 x22

Wyznacz wszystkie wartości parametru 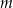, dla których równanie

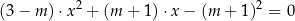
(3− m) ⋅x2 + (m + 1)⋅x − (m + 1)2 = 0

ma dwa różne rozwiązania rzeczywiste 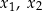x1, x2 spełniające warunek

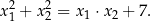
x2+ x2= x1 ⋅x2 + 7. 1 2

Dla jakich wartości parametru 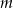suma odwrotności pierwiastków równania 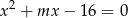x 2 + mx − 16 = 0 jest równa -4?

Wyznacz wszystkie wartości parametru 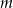, dla których jeden z pierwiastków równania

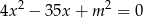
4x 2 − 35x + m2 = 0

jest kwadratem drugiego pierwiastka. Oblicz te pierwiastki.

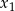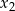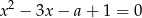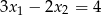Wyznacz te wartości parametru , dla których różne pierwiastki i równania x 2 − 3x − a+ 1 = 0 spełniają warunek 3x1 − 2x2 = 4 .

Strona 2 z 2