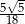Przyprostokątna trójkąta prostokątnego ma długość 6, a przeciwprostokątna ma długość 8. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 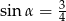 B)
B) 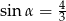 C)
C) 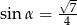 D)
D) 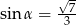
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Prostokątny
Przyprostokątna trójkąta prostokątnego ma długość 6, a przeciwprostokątna ma długość 8. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 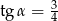 B)
B) 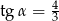 C)
C) 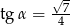 D)
D) 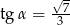
Przyprostokątna trójkąta prostokątnego ma długość 7, a przeciwprostokątna ma długość 9. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 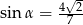 B)
B) 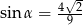 C)
C) 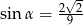 D)
D) 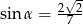
W trójkącie prostokątnym  sinus kąta
sinus kąta  jest równy
jest równy  , a przeciwprostokątna
, a przeciwprostokątna  jest o 8 dłuższa od przyprostokątnej
jest o 8 dłuższa od przyprostokątnej 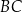 . Długość przeciwprostokątnej
. Długość przeciwprostokątnej 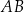 tego trójkąta jest równa
tego trójkąta jest równa
A) 18 B) 20 C) 24 D) 25
Przeciwprostokątna 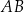 trójkąta prostokątnego
trójkąta prostokątnego 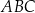 ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
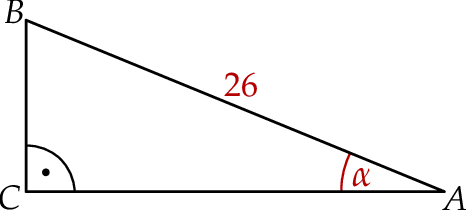
Jeżeli  jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia
jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia 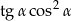 jest równa
jest równa
A) 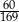 B)
B) 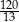 C)
C) 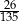 D)
D) 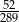
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 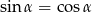 . Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
A) 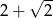 B)
B) 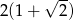 C)
C) 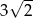 D)
D) 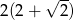
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 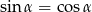 . Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
A) 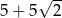 B)
B) 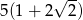 C)
C) 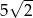 D)
D) 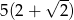
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 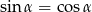 . Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
A) 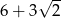 B)
B) 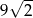 C)
C) 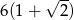 D)
D) 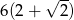
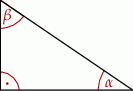
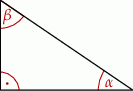
Dany jest trójkąt prostokątny o kątach ostrych  i
i 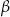 (zobacz rysunek).
(zobacz rysunek).
Wyrażenie 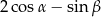 jest równe
jest równe
A) 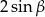 B)
B) 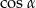 C) 0 D) 2
C) 0 D) 2
Dany jest trójkąt prostokątny o kątach ostrych  i
i 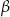 (zobacz rysunek).
(zobacz rysunek).
Wyrażenie 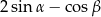 jest równe
jest równe
A) 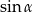 B)
B) 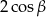 C) 0 D) 2
C) 0 D) 2
Z odcinków 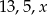 budujemy trójkąt. Będzie on prostokątny, gdy:
budujemy trójkąt. Będzie on prostokątny, gdy:
A) 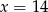 B)
B) 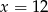 C)
C) 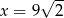 D)
D) 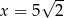
Trójkąt prostokątny równoramienny 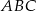 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 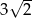 , jest podobny do trójkąta
, jest podobny do trójkąta 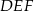 w skali
w skali 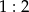 . Obwód trójkąta
. Obwód trójkąta 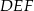 jest równy
jest równy
A) 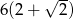 B)
B) 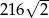 C)
C) 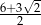 D)
D) 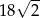
Trójkąt prostokątny równoramienny 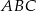 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 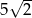 , jest podobny do trójkąta
, jest podobny do trójkąta 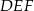 w skali
w skali 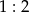 . Obwód trójkąta
. Obwód trójkąta 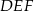 jest równy
jest równy
A) 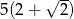 B)
B) 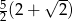 C)
C) 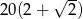 D)
D) 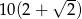
Trójkąt prostokątny równoramienny 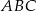 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 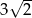 , jest podobny do trójkąta
, jest podobny do trójkąta 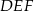 w skali
w skali 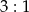 . Obwód trójkąta
. Obwód trójkąta 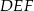 jest równy
jest równy
A) 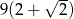 B)
B) 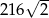 C)
C) 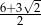 D)
D) 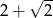
Wysokość w trójkącie prostokątnym dzieli podstawę na odcinki o długościach 3 i 5. Pole tego trójkąta jest równe:
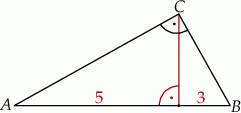
A) 15 B) 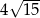 C) 16 D) za mało danych
C) 16 D) za mało danych
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 6, a jednym z jego kątów ostrych jest kąt 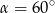 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 36 B) 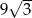 C) 18 D)
C) 18 D) 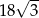
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 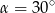 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 16 B) 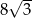 C) 8 D)
C) 8 D) 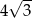
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 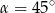 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 16 B) 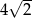 C) 8 D)
C) 8 D) 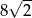
Jedna z przyprostokątnych trójkąta prostokątnego jest 3 razy dłuższa od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 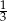 B) 3 C)
B) 3 C) 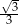 D)
D) 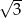
W trójkącie prostokątnym o bokach 6, 8, 10, tangens najmniejszego kąta jest równy:
A)  B)
B) 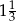 C)
C)  D)
D) 
Jedna z przyprostokątnych trójkąta prostokątnego jest 5 razy krótsza od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 5 B) 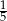 C)
C) 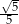 D)
D) 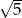
Przyprostokątne trójkąta prostokątnego mają długość 3 i 4. Wynika stąd, że tangens mniejszego z kątów ostrych jest równy
A)  B)
B)  C)
C) 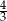 D)
D) 
Obwód trójkąta prostokątnego 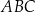 jest równy
jest równy 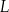 . Na boku
. Na boku 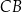 tego trójkąta obrano punkt
tego trójkąta obrano punkt 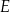 , a na boku
, a na boku 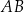 obrano punkt
obrano punkt 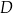 tak, że
tak, że 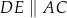 oraz
oraz 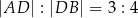 (zobacz rysunek).
(zobacz rysunek).

Obwód trójkąta 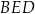 jest równy
jest równy
A) 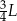 B)
B) 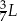 C)
C) 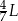 D)
D) 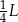
Długość boku 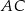 w trójkącie przedstawionym na poniższym rysunku jest równa
w trójkącie przedstawionym na poniższym rysunku jest równa
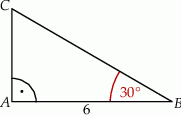
A) 3 B) 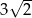 C)
C) 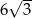 D)
D) 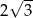
Jedna z przyprostokątnych w trójkącie prostokątnym ma długość 3 cm, a przeciwprostokątna 4 cm. Najmniejszym kątem tego trójkąta jest  . Wartość wyrażenia
. Wartość wyrażenia 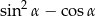 wynosi
wynosi
A) 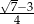 B)
B) 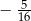 C)
C) 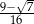 D) 1
D) 1
W trójkącie prostokątnym długości przyprostokątnych wynoszą 6 i 8. Stosunek długości odcinków, na które wysokość podzieliła przeciwprostokątną wynosi
A)  B)
B)  C)
C) 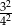 D)
D) 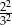
Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Poprowadzono wysokość na przeciwprostokątną. Wysokość ta podzieliła przeciwprostokątną na odcinki w stosunku
A) 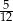 B)
B) 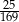 C)
C) 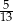 D)
D) 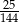
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 6,25 cm oraz 16 cm. Zatem wysokość ta ma długość
A) 15 cm B) 20 cm C) 22,25 cm D) 10 cm
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 3 cm oraz 12 cm. Zatem wysokość ta ma długość
A) 6 cm B) 20 cm C) 22,25 cm D) 10 cm
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 5,5 cm oraz 22 cm. Zatem wysokość ta ma długość
A) 15 cm B) 11 cm C) 22,25 cm D) 10 cm
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 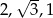 . Wtedy
. Wtedy
A) 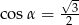 B)
B) 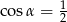 C)
C) 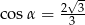 D)
D) 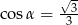
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 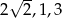 . Wtedy
. Wtedy
A) 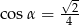 B)
B) 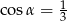 C)
C) 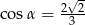 D)
D) 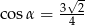
W trójkącie prostokątnym dwa dłuższe boki mają długości 5 i 7. Obwód tego trójkąta jest równy
A) 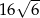 B)
B) 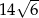 C)
C) 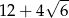 D)
D) 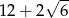
W trójkącie prostokątnym dwa dłuższe boki mają długości 7 i 9. Obwód tego trójkąta jest równy
A) 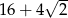 B)
B) 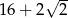 C)
C) 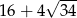 D)
D) 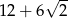
Dwa dłuższe boki trójkąta prostokątnego mają długości 3 cm oraz 4 cm. Długość najkrótszego boku tego trójkąta wynosi
A) 5 cm B) 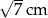 C) 2,6 cm D)
C) 2,6 cm D) 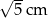
Niech  i
i 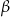 oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
A) 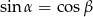 B)
B) 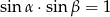 C)
C) 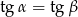 D)
D) 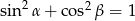
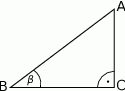
Dane są długości boków 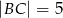 i
i 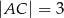 trójkąta prostokątnego
trójkąta prostokątnego  o kącie ostrym
o kącie ostrym  (zobacz rysunek).
(zobacz rysunek).
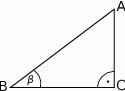
Wtedy
A) 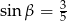 B)
B) 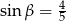 C)
C) 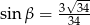 D)
D) 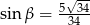
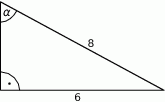
W trójkącie, przedstawionym na rysunku poniżej, cosinus kąta ostrego  jest równy
jest równy
A)  B)
B)  C)
C) 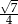 D)
D) 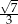
W trójkącie prostokątnym  przyprostokątne mają długość
przyprostokątne mają długość 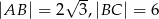 , a kąt
, a kąt 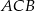 ma miarę
ma miarę  .
.
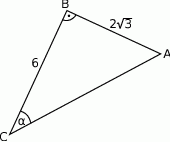
Zatem
A) 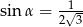 B)
B) 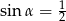 C)
C) 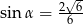 D)
D) 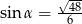
Dane są długości boków 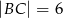 i
i 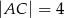 trójkąta prostokątnego
trójkąta prostokątnego  o kącie ostrym
o kącie ostrym  (zobacz rysunek).
(zobacz rysunek).
Wtedy
A) 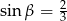 B)
B) 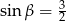 C)
C) 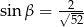 D)
D) 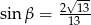
W trójkącie prostokątnym 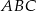 przyprostokątne mają długość
przyprostokątne mają długość 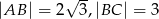 , a kąt
, a kąt 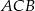 ma miarę
ma miarę  .
.
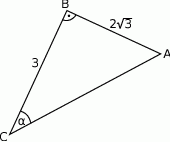
Zatem
A) 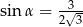 B)
B) 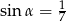 C)
C) 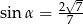 D)
D) 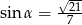
W trójkącie, przedstawionym na rysunku poniżej, sinus kąta ostrego  jest równy
jest równy
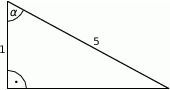
A) 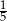 B)
B) 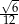 C)
C) 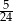 D)
D) 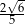
W trójkącie prostokątnym 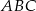 przyprostokątne mają długość
przyprostokątne mają długość 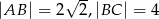 , a kąt
, a kąt 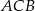 ma miarę
ma miarę  .
.
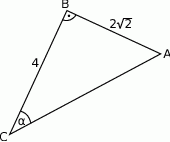
Zatem
A) 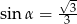 B)
B) 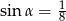 C)
C) 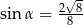 D)
D) 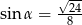
Dany jest trójkąt prostokątny (patrz rysunek).
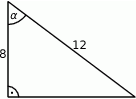
Wartość wyrażenia 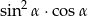 wynosi
wynosi
A) 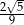 B)
B)  C)
C) 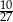 D)
D)