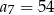Dany jest ciąg 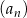 określony wzorem
określony wzorem 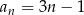 dla każdej liczby naturalnej
dla każdej liczby naturalnej 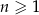 . Suma
. Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 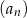 jest równa 57 dla
jest równa 57 dla  równego
równego
A) 6 B) 23 C) 5 D) 11
/Szkoła średnia/Zadania testowe/Ciągi
Dany jest ciąg 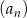 określony wzorem
określony wzorem 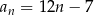 dla każdej liczby naturalnej
dla każdej liczby naturalnej 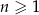 . Suma
. Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 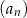 jest równa 145 dla
jest równa 145 dla  równego
równego
A) 6 B) 23 C) 5 D) 11
Miary kątów czworokąta tworzą ciąg arytmetyczny o różnicy 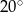 . Najmniejszy kąt tego czworokąta ma miarę
. Najmniejszy kąt tego czworokąta ma miarę
A) 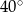 B)
B) 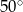 C)
C) 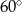 D)
D) 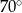
Miary kątów czworokąta tworzą ciąg arytmetyczny o różnicy 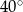 . Najmniejszy kąt tego czworokąta ma miarę
. Najmniejszy kąt tego czworokąta ma miarę
A) 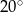 B)
B) 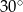 C)
C) 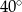 D)
D) 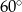
Trzy liczby tworzą ciąg arytmetyczny. Suma tych liczb jest równa 18. Drugi wyraz tego ciągu jest równy
A) 6 B) 5 C) 4 D) 3
Trzy liczby tworzą ciąg arytmetyczny. Suma tych liczb jest równa 21. Drugi wyraz tego ciągu jest równy
A) 6 B) 5 C) 4 D) 7
Trzy liczby tworzą ciąg arytmetyczny. Suma tych liczb jest równa 24. Drugi wyraz tego ciągu jest równy
A) 6 B) 5 C) 8 D) 7
Wyrazami ciągu 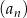 danego wzorem
danego wzorem 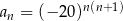
A) są zawsze liczby mniejsze od 1 B) są zawsze liczby dodatnie
C) są zawsze liczby ujemne D) są zarówno liczby dodatnie, jak i ujemne
Wyrazami ciągu 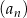 danego wzorem
danego wzorem 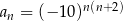
A) są zawsze liczby mniejsze od 1 B) są zawsze liczby dodatnie
C) są zawsze liczby ujemne D) są zarówno liczby dodatnie, jak i ujemne
Drugi wyraz ciągu arytmetycznego jest równy 12, a trzeci wyraz jest równy 5. Wzór na ogólny wyraz tego ciągu to
A) 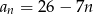 B)
B) 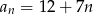 C)
C) 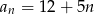 D)
D) 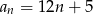
Drugi wyraz ciągu arytmetycznego jest równy 5, a trzeci wyraz jest równy 12. Wzór na ogólny wyraz tego ciągu to
A) 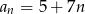 B)
B) 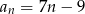 C)
C) 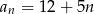 D)
D) 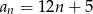
Drugi wyraz ciągu arytmetycznego jest równy 10, a trzeci wyraz jest równy 6. Wzór na ogólny wyraz tego ciągu to
A) 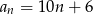 B)
B) 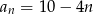 C)
C) 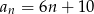 D)
D) 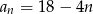
Dwa wyrazy ciągu arytmetycznego o wyrazach całkowitych są równe 200 i 101. Różnica tego ciągu może być równa
A) 5 B) 18 C) 11 D) 199
Dwa wyrazy ciągu arytmetycznego o wyrazach całkowitych są równe 319 i 409. Różnica tego ciągu może być równa
A) 12 B) 18 C) 11 D) 19
Ciąg 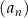 jest określony wzorem
jest określony wzorem 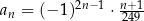 dla każdej liczby naturalnej
dla każdej liczby naturalnej 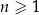 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wśród wyrazów ciągu 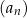 są zarówno liczby dodatnie jak i liczby ujemne. są zarówno liczby dodatnie jak i liczby ujemne. | P | F |
Wśród wyrazów ciągu 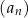 jest co najmniej 10 liczb całkowitych. jest co najmniej 10 liczb całkowitych. | P | F |
Ciąg 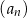 określony jest w następujący sposób
określony jest w następujący sposób 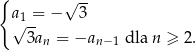 Suma wszystkich wyrazów ciągu
Suma wszystkich wyrazów ciągu 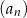 jest równa
jest równa
A) 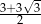 B)
B) 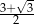 C)
C) 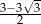 D)
D) 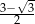
Czterowyrazowy ciąg 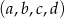 jest arytmetyczny i suma jego wyrazów jest równa 27. Suma
jest arytmetyczny i suma jego wyrazów jest równa 27. Suma 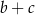 równa
równa
A) 27 B) 13,5 C) 17 D) 9
W ciągu arytmetycznym 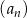 , określonym dla
, określonym dla 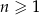 , wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15. Jednym z wyrazów tego ciągu jest liczba
, wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15. Jednym z wyrazów tego ciągu jest liczba
A) 2023 B) 1945 C) 1410 D) 2000
Ciąg 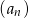 jest określony w następujący sposób:
jest określony w następujący sposób: 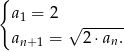 Czwarty wyraz ciągu
Czwarty wyraz ciągu 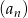 jest równy
jest równy
A) 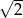 B) 2 C)
B) 2 C) 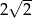 D)
D) 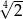
Ciąg 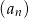 jest określony w następujący sposób:
jest określony w następujący sposób: 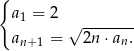 Trzeci wyraz ciągu
Trzeci wyraz ciągu 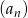 jest równy
jest równy
A) 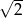 B) 2 C)
B) 2 C) 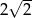 D)
D) 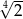
Jeżeli suma częściowa ciągu geometrycznego wyraża się wzorem 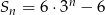 , gdzie
, gdzie 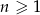 , to czwarty wyraz tego ciągu jest równy
, to czwarty wyraz tego ciągu jest równy
A) 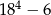 B) 480 C) 324 D) 156
B) 480 C) 324 D) 156
Jeżeli suma częściowa ciągu geometrycznego wyraża się wzorem 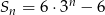 , gdzie
, gdzie 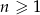 , to trzeci wyraz tego ciągu jest równy
, to trzeci wyraz tego ciągu jest równy
A) 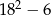 B) 108 C) 324 D) 156
B) 108 C) 324 D) 156
Jeżeli suma częściowa ciągu geometrycznego wyraża się wzorem 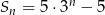 , gdzie
, gdzie 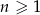 , to czwarty wyraz tego ciągu jest równy
, to czwarty wyraz tego ciągu jest równy
A) 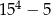 B) 270 C) 400 D) 130
B) 270 C) 400 D) 130
Ciąg 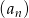 określony jest wzorem
określony jest wzorem 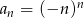 dla
dla 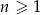 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 232 B) 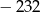 C) 96 D)
C) 96 D) 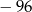
Wszystkie wyrazy ciągu geometrycznego 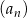 określonego dla
określonego dla 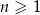 są dodatnie i
są dodatnie i 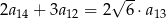 . Stąd wynika, że iloraz
. Stąd wynika, że iloraz 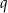 tego ciągu jest równy
tego ciągu jest równy
A) 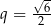 B)
B) 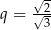 C)
C) 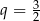 D)
D) 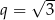
Dany jest ciąg arytmetyczny 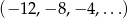 . Czterdziesty wyraz tego ciągu jest równy
. Czterdziesty wyraz tego ciągu jest równy
A) -148 B) 144 C) 148 D) 166
W ciągu arytmetycznym 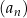 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 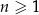 , dane są wyrazy:
, dane są wyrazy: 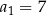 oraz
oraz 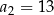 . Wyraz
. Wyraz 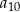 jest równy
jest równy
A) 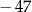 B) 52 C) 61 D) 67
B) 52 C) 61 D) 67
Dany jest ciąg arytmetyczny 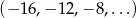 . Trzydziesty wyraz tego ciągu jest równy
. Trzydziesty wyraz tego ciągu jest równy
A) -132 B) -136 C) 100 D) 104
Osiemnasty wyraz ciągu arytmetycznego 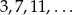 jest równy:
jest równy:
A) 71 B) 68 C) 75 D) 72
Dany jest ciąg arytmetyczny 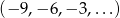 . Czterdziesty wyraz tego ciągu jest równy
. Czterdziesty wyraz tego ciągu jest równy
A) -111 B) 126 C) 111 D) 108
Dany jest ciąg 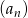 , w którym
, w którym 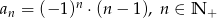 . Jeśli
. Jeśli 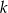 jest liczbą naturalną nieparzystą, to:
jest liczbą naturalną nieparzystą, to:
A) 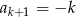 B)
B) 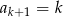 C)
C) 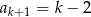 D)
D) 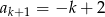
Dany jest ciąg 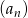 , w którym
, w którym 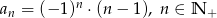 . Jeśli
. Jeśli 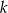 jest liczbą naturalną parzystą, to:
jest liczbą naturalną parzystą, to:
A) 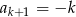 B)
B) 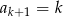 C)
C) 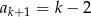 D)
D) 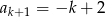
Długość boku, długość przekątnej oraz pole kwadratu są kolejnymi wyrazami ciągu geometrycznego. Iloraz tego ciągu jest
A) liczbą niewymierną B) liczbą całkowitą
C) liczbą z przedziału 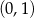 D) wymierną niecałkowitą
D) wymierną niecałkowitą
Długość boku, długość przekątnej oraz pole kwadratu są kolejnymi wyrazami ciągu geometrycznego. Pierwszy wyraz tego ciągu jest
A) liczbą niewymierną B) liczbą całkowitą
C) liczbą z przedziału 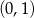 D) wymierną niecałkowitą
D) wymierną niecałkowitą
Trzywyrazowy ciąg 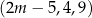 jest arytmetyczny. Dokończ zdanie tak, aby było prawdziwe. Ten ciąg jest
jest arytmetyczny. Dokończ zdanie tak, aby było prawdziwe. Ten ciąg jest
| A) rosnący, | B) malejący |
oraz
1) 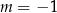 , , | 2) 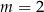 , , | 3) 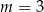 . . |
Wyraz ogólny ciągu 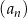 ma postać
ma postać 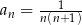 , gdzie
, gdzie 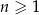 . Wobec tego
. Wobec tego
A) 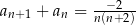 B)
B) 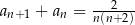
C) 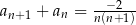 D)
D) 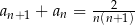
Wyraz ogólny ciągu 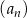 ma postać
ma postać 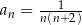 , gdzie
, gdzie 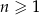 . Wobec tego
. Wobec tego
A) 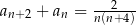 B)
B) 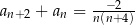
C) 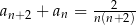 D)
D) 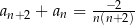
W ciągu 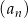 określonym dla każdej liczby
określonym dla każdej liczby 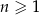 jest spełniony warunek
jest spełniony warunek 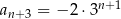 . Wtedy
. Wtedy
A) 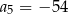 B)
B) 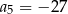 C)
C) 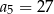 D)
D) 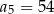
W ciągu 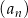 określonym dla każdej liczby
określonym dla każdej liczby 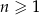 jest spełniony warunek
jest spełniony warunek 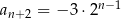 . Wtedy
. Wtedy
A) 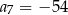 B)
B) 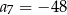 C)
C) 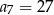 D)
D)