Długość tworzącej stożka jest równa średnicy jego podstawy. Pole powierzchni bocznej stożka jest równe 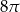 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 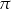 B)
B) 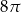 C)
C) 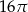 D)
D) 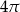
/Szkoła średnia/Zadania testowe/Geometria/Stereometria
Długość tworzącej stożka jest dwa razy dłuższa niż średnica jego podstawy. Pole powierzchni bocznej stożka jest równe 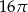 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 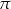 B)
B) 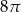 C)
C) 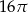 D)
D) 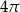
Długość tworzącej stożka jest 4 razy większa niż długość średnicy jego podstawy. Pole powierzchni bocznej stożka jest równe 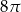 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 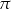 B)
B) 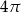 C)
C) 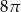 D)
D) 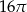
Półkole o promieniu 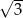 cm zwinięto w stożek.
cm zwinięto w stożek.
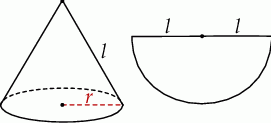
Wysokość tego stożka jest równa
A) 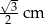 B)
B) 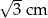 C) 3 cm D) 1,5 cm
C) 3 cm D) 1,5 cm
Jeżeli promień podstawy stożka zwiększymy o 20%, a wysokość zmniejszymy o 20%, to objętość stożka
A) nie zmieni się B) zwiększy się o 15,2%
C) zwiększy się o 1,52% D) zmniejszy się o 4%
Jeżeli promień podstawy stożka zwiększymy o 10%, a wysokość zmniejszymy o 10%, to objętość stożka
A) zwiększy się o 0,89% B) nie zmieni się
C) zmniejszy się o 0,89% D) zwiększy się o 8,9%
Jeżeli promień podstawy stożka zmniejszymy o 20%, a wysokość zwiększymy o 20%, to objętość stożka
A) nie zmieni się B) zwiększy się o 2,32%
C) zmniejszy się o 76,8% D) zmniejszy się o 23,2%
Średnica kuli 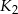 jest dwa razy dłuższa od średnicy kuli
jest dwa razy dłuższa od średnicy kuli 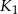 . Ile razy objętość kuli
. Ile razy objętość kuli 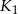 jest mniejsza od objętości kuli
jest mniejsza od objętości kuli 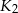 ?
?
A) 2 razy B) 3 razy C) 4 razy D) 8 razy
Średnica kuli 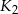 jest trzy razy krótsza od średnicy kuli
jest trzy razy krótsza od średnicy kuli 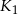 . Ile razy objętość kuli
. Ile razy objętość kuli 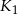 jest większa od objętości kuli
jest większa od objętości kuli 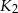 ?
?
A) 27 razy B) 9 razy C) 6 razy D) 3 razy
Średnica kuli 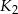 jest cztery razy dłuższa od średnicy kuli
jest cztery razy dłuższa od średnicy kuli 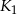 . Ile razy objętość kuli
. Ile razy objętość kuli 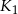 jest mniejsza od objętości kuli
jest mniejsza od objętości kuli 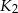 ?
?
A) 4 razy B) 64 razy C) 32 razy D) 16 razy
Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
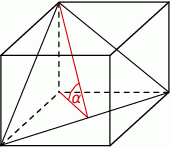
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 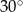 B)
B) 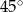 C)
C) 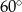 D)
D) 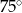
Przekątna podstawy graniastosłupa prawidłowego czworokątnego ma długość 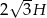 , gdzie
, gdzie 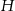 jest wysokością tego graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
jest wysokością tego graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
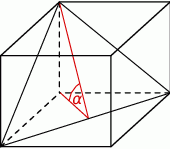
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 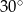 B)
B) 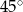 C)
C) 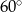 D)
D) 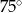
Stożki 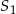 oraz
oraz 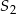 mają równe wysokości. Promień podstawy stożka
mają równe wysokości. Promień podstawy stożka 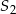 jest 4 razy dłuższy od promienia stożka
jest 4 razy dłuższy od promienia stożka 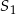 . Wobec tego objętość stożka
. Wobec tego objętość stożka 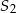 jest
jest
A) 4 razy większa od objętości stożka 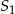
B) o 150% większa od objętości stożka 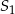
C) o 300% większa od objętości stożka 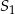
D) o 1500% większa od objętości stożka 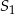
Stożki 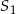 oraz
oraz 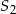 mają równe promienie podstawy. Wysokość stożka
mają równe promienie podstawy. Wysokość stożka 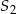 jest 4 razy dłuższa od wysokości stożka
jest 4 razy dłuższa od wysokości stożka 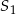 . Wobec tego objętość stożka
. Wobec tego objętość stożka 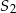 jest
jest
A) 4 razy większa od objętości stożka 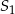
B) o 150% większa od objętości stożka 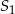
C) o 400% większa od objętości stożka 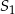
D) 0 1500% większa od objętości stożka 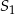
Stożki 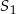 oraz
oraz 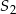 mają równe wysokości. Promień podstawy stożka
mają równe wysokości. Promień podstawy stożka 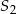 jest 2 razy dłuższy od promienia stożka
jest 2 razy dłuższy od promienia stożka 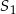 . Wobec tego objętość stożka
. Wobec tego objętość stożka 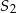 jest
jest
A) 4 razy większa od objętości stożka 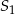
B) o 150% większa od objętości stożka 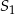
C) o 400% większa od objętości stożka 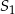
D) o 1500% większa od objętości stożka 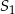
Podstawą graniastosłupa prostego jest romb o przekątnych długości 7 cm i 10 cm. Wysokość tego graniastosłupa jest krótsza od dłuższej przekątnej rombu o 2 cm. Wtedy objętość graniastosłupa jest równa
A) 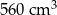 B)
B) 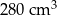 C)
C) 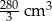 D)
D) 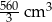
Podstawą graniastosłupa prostego jest romb o przekątnych długości 8 cm i 12 cm. Wysokość tego graniastosłupa jest dwa razy krótsza od dłuższej przekątnej rombu w podstawie. Wtedy objętość graniastosłupa jest równa
A) 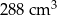 B)
B) 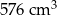 C)
C) 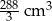 D)
D) 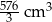
Wysokość graniastosłupa prawidłowego sześciokątnego jest równa 6 (zobacz rysunek).
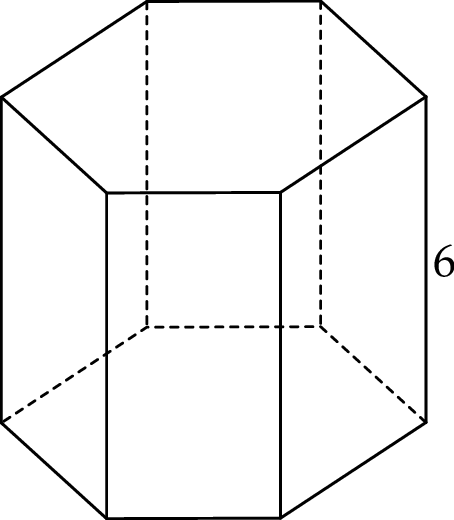
Pole podstawy tego graniastosłupa jest równe 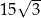 . Pole jednej ściany bocznej tego graniastosłupa jest równe
. Pole jednej ściany bocznej tego graniastosłupa jest równe
A) 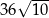 B) 60 C)
B) 60 C) 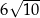 D) 360
D) 360
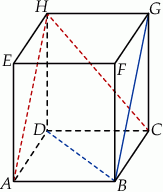
Podstawą graniastosłupa prostego czworokątnego 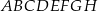 jest kwadrat
jest kwadrat 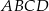 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 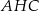 między przekątnymi sąsiednich ścian bocznych ma miarę
między przekątnymi sąsiednich ścian bocznych ma miarę 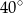 . Kąt
. Kąt 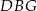 między przekątną podstawy, a przekątną ściany bocznej ma miarę
między przekątną podstawy, a przekątną ściany bocznej ma miarę
A) 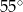 B)
B) 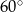 C)
C) 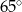 D)
D) 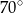
Podstawą graniastosłupa prostego czworokątnego 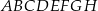 jest kwadrat
jest kwadrat 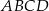 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 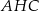 między przekątnymi sąsiednich ścian bocznych ma miarę
między przekątnymi sąsiednich ścian bocznych ma miarę 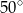 . Kąt
. Kąt 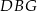 między przekątną podstawy, a przekątną ściany bocznej ma miarę
między przekątną podstawy, a przekątną ściany bocznej ma miarę
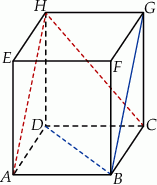
A) 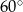 B)
B) 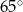 C)
C) 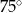 D)
D) 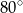
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4. Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 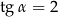 .
.
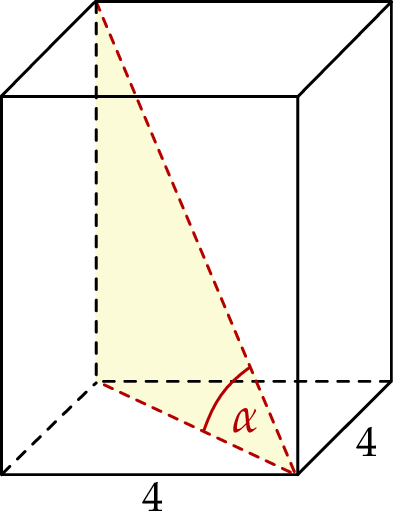
Wysokość tego graniastosłupa jest równa
A) 2 B) 8 C) 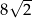 D)
D) 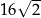
Podstawą prostopadłościanu jest prostokąt o wymiarach 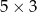 , a jego pole powierzchni całkowitej jest równe 94. Wysokość tego prostopadłościanu ma długość
, a jego pole powierzchni całkowitej jest równe 94. Wysokość tego prostopadłościanu ma długość
A) 2 B) 3 C) 4 D) 5
Ostrosłup prawidłowy ma 2024 ściany boczne. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 2025 B) 2026 C) 4048 D) 4052
Pole powierzchni całkowitej pewnego stożka jest 3 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 2 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 12 B) 11 C) 24 D) 22
Pole powierzchni całkowitej pewnego stożka jest 4 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 3 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 42 B) 45 C) 48 D) 52
Przekątna sześcianu jest o 2 dłuższa od przekątnej ściany sześcianu. Wówczas krawędź sześcianu jest równa
A) 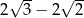 B)
B) 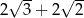 C)
C) 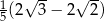 D)
D) 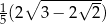
Przekątna sześcianu jest o 3 większa od przekątnej ściany sześcianu. Wówczas krawędź sześcianu jest równa
A) 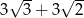 B)
B) 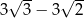 C)
C) 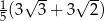 D)
D) 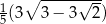
Przekątna sześcianu jest o 5 większa od przekątnej ściany sześcianu. Wówczas krawędź sześcianu jest równa
A) 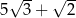 B)
B) 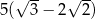 C)
C) 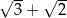 D)
D) 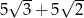
Ostrosłup ma 7 wierzchołków. Liczba jego ścian jest równa
A) 6 B) 7 C) 11 D) 12
Ostrosłup ma 8 wierzchołków. Liczba jego ścian jest równa
A) 6 B) 7 C) 8 D) 12
Ostrosłup ma 10 wierzchołków. Liczba jego ścian jest równa
A) 8 B) 9 C) 10 D) 6
Pole powierzchni bocznej walca jest równe 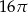 , a promień jego podstawy ma długość 2. Wysokość tego walca jest równa
, a promień jego podstawy ma długość 2. Wysokość tego walca jest równa
A) 4 B) 8 C) 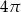 D)
D) 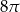
Pole powierzchni bocznej walca jest równe 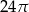 , a promień jego podstawy ma długość 4. Wysokość tego walca jest równa
, a promień jego podstawy ma długość 4. Wysokość tego walca jest równa
A) 6 B) 3 C) 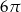 D)
D) 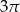
Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy 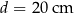 , wysokości
, wysokości 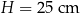 i tworzącej
i tworzącej 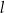 . Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską
. Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską 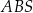 o kształcie wycinka koła o promieniu
o kształcie wycinka koła o promieniu 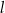 i środku
i środku 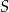 . Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek
. Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek 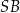 z odcinkiem
z odcinkiem 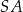 .
.

Kąt rozwarcia stożka, którego powierzchnią boczną jest czapeczka, ma miarę (w zaokrągleniu do 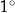 )
)
A) 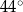 B)
B) 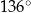 C)
C) 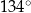 D)
D) 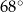
Dwa stożki o takich samych podstawach połączono podstawami w taki sposób jak na rysunku. Stosunek wysokości tych stożków jest równy 3 : 2. Objętość stożka o krótszej wysokości jest równa 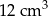 .
.
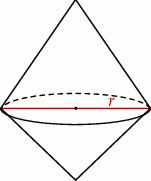
Objętość bryły utworzonej z połączonych stożków jest równa
A) 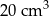 B)
B) 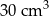 C)
C) 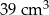 D)
D) 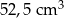
Dwa stożki o takich samych podstawach połączono podstawami w taki sposób jak na rysunku. Stosunek wysokości tych stożków jest równy 3 : 4. Objętość stożka o dłuższej wysokości jest równa 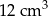 .
.
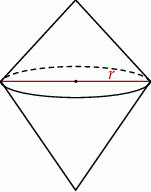
Objętość bryły utworzonej z połączonych stożków jest równa
A) 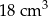 B)
B) 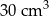 C)
C) 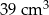 D)
D) 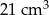
Suma liczby wierzchołków i liczby krawędzi graniastosłupa może być równa
A) 2017 B) 2016 C) 2015 D) 2014
Suma długości wszystkich krawędzi sześcianu jest równa 24. Pole powierzchni tego sześcianu jest równe
A) 4 B) 16 C) 24 D) 8
Suma długości wszystkich krawędzi sześcianu jest równa 96 cm. Pole powierzchni całkowitej tego sześcianu jest równe
A) 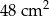 B)
B) 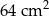 C)
C) 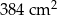 D)
D) 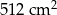
Suma długości wszystkich krawędzi sześcianu jest równa 108 cm. Pole powierzchni całkowitej tego sześcianu jest równe
A) 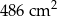 B)
B) 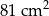 C)
C) 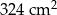 D)
D)