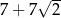Pierwszy wyraz rosnącego ciągu geometrycznego 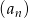 jest równy
jest równy 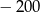 , a iloraz tego ciągu należy do zbioru
, a iloraz tego ciągu należy do zbioru 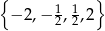 . Wobec tego iloraz ciągu
. Wobec tego iloraz ciągu 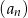 jest równy
jest równy
A) -2 B) 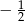 C)
C) 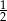 D) 2
D) 2
/Szkoła średnia/Zadania testowe/Ciągi/Geometryczny
Pierwszy wyraz malejącego ciągu geometrycznego 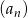 jest równy
jest równy 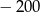 , a iloraz tego ciągu należy do zbioru
, a iloraz tego ciągu należy do zbioru 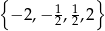 . Wobec tego iloraz ciągu
. Wobec tego iloraz ciągu 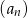 jest równy
jest równy
A) -2 B) 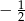 C)
C) 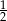 D) 2
D) 2
W ciągu geometrycznym 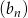 wyraz
wyraz 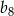 jest równy
jest równy 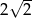 , zaś iloraz tego ciągu ma wartość
, zaś iloraz tego ciągu ma wartość 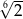 . Wobec tego
. Wobec tego
A) 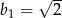 B)
B) 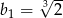 C)
C) 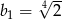 D)
D) 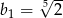
W ciągu geometrycznym 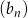 wyraz
wyraz 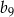 jest równy
jest równy 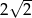 , zaś iloraz tego ciągu ma wartość
, zaś iloraz tego ciągu ma wartość 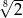 . Wobec tego
. Wobec tego
A) 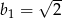 B)
B) 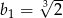 C)
C) 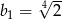 D)
D) 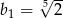
W ciągu geometrycznym 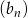 wyraz
wyraz 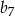 jest równy
jest równy 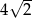 , zaś iloraz tego ciągu ma wartość
, zaś iloraz tego ciągu ma wartość 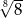 . Wobec tego
. Wobec tego
A) 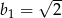 B)
B) 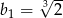 C)
C) 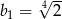 D)
D) 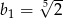
W ciągu geometrycznym 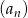 dane są:
dane są: 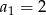 i
i 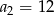 . Wtedy
. Wtedy
A) 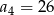 B)
B) 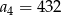 C)
C) 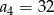 D)
D) 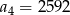
W ciągu geometrycznym 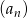 dane są:
dane są: 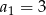 i
i 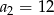 . Wtedy
. Wtedy
A) 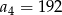 B)
B) 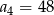 C)
C) 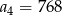 D)
D) 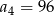
W ciągu geometrycznym 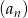 dane są:
dane są: 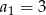 i
i 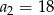 . Wtedy
. Wtedy
A) 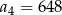 B)
B) 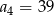 C)
C) 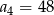 D)
D) 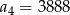
W ciągu geometrycznym 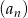 dane są:
dane są: 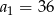 i
i 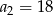 . Wtedy
. Wtedy
A) 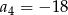 B)
B) 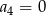 C)
C) 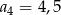 D)
D) 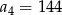
Jeżeli w ciągu geometrycznym 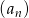 pierwszy wyraz ciągu jest równy
pierwszy wyraz ciągu jest równy 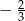 , a drugi wynosi 2, to
, a drugi wynosi 2, to
A) 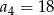 B)
B) 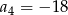 C)
C) 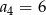 D)
D) 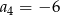
Jeżeli w ciągu geometrycznym 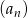 pierwszy wyraz ciągu jest równy
pierwszy wyraz ciągu jest równy 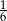 , a drugi wynosi
, a drugi wynosi 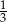 , to
, to
A) 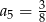 B)
B) 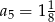 C)
C) 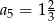 D)
D) 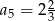
Czterowyrazowy ciąg 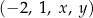 jest geometryczny. Suma wszystkich wyrazów tego ciągu jest równa
jest geometryczny. Suma wszystkich wyrazów tego ciągu jest równa
A) 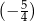 B)
B) 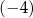 C)
C) 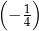 D)
D) 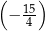
Dany jest ciąg geometryczny 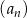 , określony dla
, określony dla 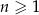 , w którym
, w którym 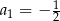 ,
, 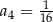 . Suma czterech początkowych wyrazów ciągu
. Suma czterech początkowych wyrazów ciągu 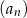 jest równa
jest równa
A) 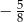 B)
B) 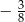 C)
C) 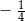 D)
D) 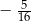
Ciąg geometryczny 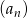 jest określony wzorem
jest określony wzorem 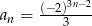 dla
dla 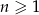 . Suma jedenastu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma jedenastu początkowych kolejnych wyrazów tego ciągu jest równa
A) 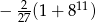 B)
B) 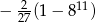 C)
C) 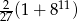 D)
D) 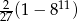
Dany jest ciąg geometryczny 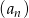 , w którym
, w którym 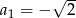 ,
, 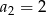 ,
, 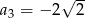 . Dziesiąty wyraz tego ciągu, czyli
. Dziesiąty wyraz tego ciągu, czyli 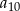 , jest równy
, jest równy
A) 32 B) 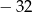 C)
C) 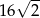 D)
D) 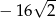
Dany jest ciąg geometryczny 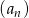 , w którym
, w którym 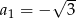 ,
, 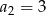 ,
, 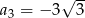 . Dziewiąty wyraz tego ciągu, czyli
. Dziewiąty wyraz tego ciągu, czyli 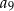 , jest równy
, jest równy
A) 243 B) 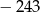 C)
C) 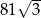 D)
D) 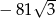
Dany jest ciąg geometryczny o wyrazie ogólnym 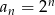 , dla
, dla 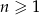 . Liczba wyrazów tego ciągu mniejszych od 64 jest równa
. Liczba wyrazów tego ciągu mniejszych od 64 jest równa
A) 6 B) 5 C) 4 D) 3
Dany jest ciąg geometryczny o wyrazie ogólnym 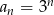 , gdzie
, gdzie 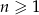 . Liczba wyrazów tego ciągu mniejszych od 243 jest równa
. Liczba wyrazów tego ciągu mniejszych od 243 jest równa
A) 6 B) 5 C) 4 D) 3
Dany jest ciąg geometryczny o wyrazie ogólnym 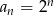 , gdzie
, gdzie 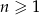 . Liczba wyrazów tego ciągu mniejszych od 128 jest równa
. Liczba wyrazów tego ciągu mniejszych od 128 jest równa
A) 6 B) 5 C) 4 D) 7
Dany jest nieskończony rosnący ciąg geometryczny 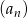 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 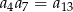 B)
B) 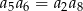 C)
C) 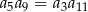 D)
D) 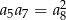
Pięć liczb tworzy ciąg geometryczny. Iloczyn tych liczb jest równy 59049. Trzeci wyraz tego ciągu jest równy
A) 243 B) 9 C) 3 D) 27
Siedem liczb tworzy ciąg geometryczny. Iloczyn tych liczb jest równy 2187. Czwarty wyraz tego ciągu jest równy
A) 243 B) 9 C) 3 D) 27
Liczby 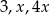 są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
A) 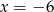 B)
B) 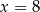 C)
C) 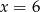 D)
D) 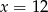
Liczby 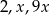 są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
A) 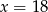 B)
B) 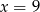 C)
C) 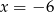 D)
D) 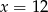
Dany jest ciąg geometryczny 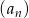 , określony dla
, określony dla 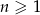 , o którym wiemy, że:
, o którym wiemy, że: 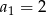 i
i 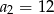 . Wtedy
. Wtedy 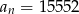 dla
dla
A) 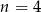 B)
B) 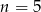 C)
C) 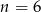 D)
D) 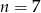
Dany jest ciąg geometryczny 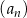 , określony dla
, określony dla 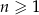 , o którym wiemy, że:
, o którym wiemy, że: 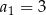 i
i 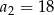 . Wtedy
. Wtedy 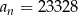 dla
dla
A) 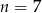 B)
B) 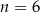 C)
C) 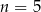 D)
D) 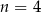
Jaką liczbę można wstawić pomiędzy 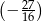 i
i 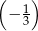 , aby z danymi liczbami tworzyła ciąg geometryczny?
, aby z danymi liczbami tworzyła ciąg geometryczny?
A) 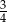 B)
B) 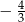 C)
C) 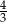 D)
D) 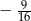
Jaką liczbę można wstawić pomiędzy liczby 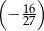 i
i 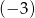 , aby z danymi liczbami tworzyła ciąg geometryczny?
, aby z danymi liczbami tworzyła ciąg geometryczny?
A) 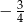 B)
B) 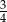 C)
C) 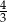 D)
D) 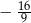
W ciągu geometrycznym rosnącym 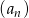 wyraz
wyraz 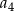 jest równy 4, a wyraz
jest równy 4, a wyraz 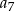 jest równy 32. Wskaż wzór na
jest równy 32. Wskaż wzór na  -ty wyraz ciągu
-ty wyraz ciągu
A) 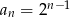 B)
B) 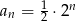 C)
C) 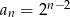 D)
D) 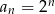
W ciągu geometrycznym rosnącym 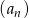 wyraz
wyraz 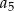 jest równy 4, a wyraz
jest równy 4, a wyraz 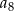 jest równy 32. Wskaż wzór na
jest równy 32. Wskaż wzór na  -ty wyraz ciągu
-ty wyraz ciągu
A) 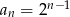 B)
B) 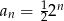 C)
C) 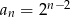 D)
D) 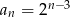
W ciągu geometrycznym rosnącym 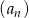 wyraz
wyraz 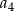 jest równy 6, a wyraz
jest równy 6, a wyraz 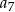 jest równy 48. Wskaż wzór na
jest równy 48. Wskaż wzór na  -ty wyraz ciągu
-ty wyraz ciągu
A) 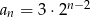 B)
B) 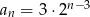 C)
C) 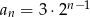 D)
D) 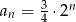
Wzorem ogólnym ciągu geometrycznego w którym 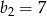 i
i 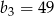 jest:
jest:
A) 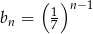 B)
B) 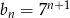 C)
C) 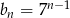 D)
D) 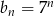
Wzorem ogólnym ciągu geometrycznego w którym 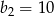 i
i 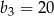 jest:
jest:
A) 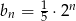 B)
B) 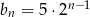 C)
C) 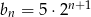 D)
D) 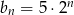
Liczby 2,6 są dwoma początkowymi wyrazami ciągu geometrycznego. Do wyrazów tego ciągu nie należy liczba
A) 162 B) 54 C) 18 D) 9
Liczby 4,12 są dwoma początkowymi wyrazami ciągu geometrycznego. Do wyrazów tego ciągu nie należy liczba
A) 36 B) 108 C) 48 D) 324
Liczby 3,12 są dwoma początkowymi wyrazami ciągu geometrycznego. Do wyrazów tego ciągu nie należy liczba
A) 192 B) 96 C) 768 D) 48
Suma szeregu geometrycznego: 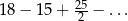 jest równa
jest równa
A) 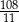 B) 33 C)
B) 33 C) 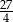 D) 108
D) 108
Dany jest rosnący ciąg geometryczny 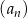 , określony dla liczb naturalnych
, określony dla liczb naturalnych 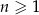 , o wyrazach dodatnich. Jeśli
, o wyrazach dodatnich. Jeśli 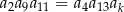 , to
, to 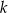 jest równe
jest równe
A) 8 B) 7 C) 6 D) 5
Ciąg geometryczny 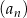 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 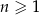 , jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek
, jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek 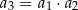 . Niech
. Niech 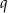 oznacza iloraz ciągu
oznacza iloraz ciągu 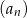 . Wtedy
. Wtedy
A) 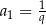 B)
B) 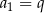 C)
C) 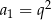 D)
D) 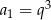
Ciąg geometryczny 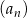 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 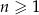 , jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek
, jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek 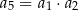 . Niech
. Niech 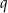 oznacza iloraz ciągu
oznacza iloraz ciągu 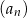 . Wtedy
. Wtedy
A) 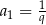 B)
B) 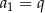 C)
C) 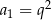 D)
D) 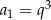
Dany jest ciąg geometryczny 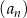 , określony dla
, określony dla 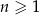 , w którym
, w którym 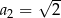 ,
, 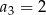 . Suma sześciu początkowych wyrazów ciągu
. Suma sześciu początkowych wyrazów ciągu 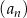 jest równa
jest równa
A) 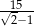 B)
B) 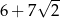 C)
C) 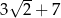 D)
D)