Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa  . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A)  B)
B)  C)
C)  D) 7
D) 7
/Szkoła średnia/Zadania testowe/Ciągi/Geometryczny
Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy mniejszy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 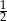 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 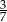 B)
B) 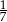 C)
C)  D) 7
D) 7
Miary kątów czworokąta tworzą ciąg geometryczny o ilorazie 2. Największy kąt tego czworokąta ma miarę
A) 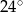 B)
B) 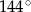 C)
C) 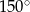 D)
D) 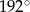
Miary kątów trójkąta tworzą ciąg geometryczny o ilorazie 4. Miara największego z nich jest równa
A) 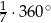 B)
B) 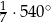 C)
C) 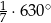 D)
D) 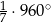
Dany jest ciąg geometryczny 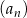 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 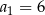 . Jeżeli
. Jeżeli 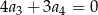 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 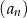 jest
jest
A) 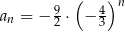 B)
B) 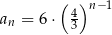 C)
C) 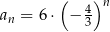 D)
D) 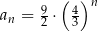
Dany jest ciąg geometryczny 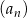 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 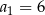 . Jeżeli
. Jeżeli 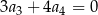 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 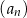 jest
jest
A) 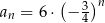 B)
B) 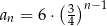 C)
C) 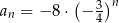 D)
D) 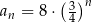
Dany jest ciąg geometryczny 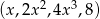 o wyrazach nieujemnych. Wtedy
o wyrazach nieujemnych. Wtedy
A) 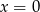 B)
B) 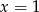 C)
C) 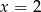 D)
D) 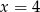
Dany jest ciąg geometryczny 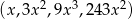 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 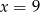 B)
B) 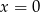 C)
C) 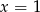 D)
D) 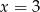
Dany jest ciąg geometryczny 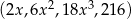 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 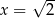 B)
B) 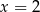 C)
C) 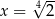 D)
D) 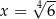
Ciąg 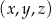 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że 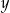 jest równe
jest równe
A) 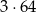 B)
B) 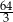 C) 4 D) 3
C) 4 D) 3
Ciąg 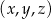 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że 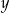 jest równe
jest równe
A) 81 B) 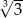 C) 9 D) 3
C) 9 D) 3
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 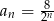 , gdzie
, gdzie 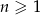 jest równy
jest równy
A) 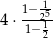 B)
B) 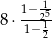 C)
C) 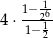 D)
D) 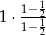
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 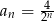 , gdzie
, gdzie 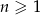 jest równy
jest równy
A) 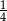 B)
B) 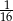 C)
C) 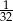 D)
D) 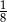
Nieskończony ciąg geometryczny 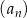 jest określony w następujący sposób:
jest określony w następujący sposób: 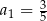 oraz
oraz 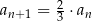 dla
dla 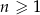 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 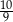 C)
C) 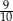 D)
D) 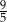
Nieskończony ciąg geometryczny 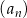 jest określony w następujący sposób:
jest określony w następujący sposób: 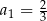 oraz
oraz 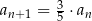 dla
dla 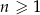 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 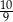 C)
C) 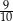 D)
D) 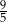
Ciąg 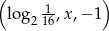 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 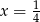 B)
B) 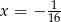 C)
C) 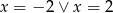 D)
D) 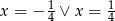
Ciąg 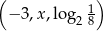 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 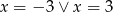 B)
B) 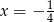 C)
C) 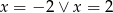 D)
D) 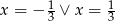
Ciąg 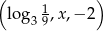 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 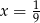 B)
B) 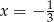 C)
C) 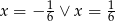 D)
D) 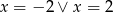
Trzywyrazowy ciąg 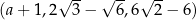 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 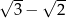 B)
B) 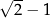 C)
C) 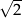 D)
D) 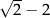
Liczby 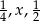 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 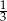 B)
B)  C)
C) 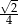 D)
D) 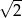
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 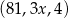 . Stąd wynika, że
. Stąd wynika, że
A) 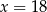 B)
B) 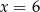 C)
C) 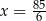 D)
D) 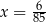
Ciąg 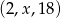 jest ciągiem geometrycznym tylko wtedy, gdy
jest ciągiem geometrycznym tylko wtedy, gdy
A) 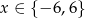 B)
B) 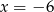 C)
C) 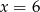 D)
D) 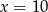
Ciąg 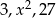 jest ciągiem geometrycznym, gdy
jest ciągiem geometrycznym, gdy
A) tylko 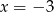 B) tylko
B) tylko 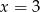 C)
C) 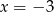 lub
lub 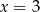 D)
D) 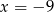 lub
lub 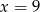
Liczby 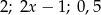 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla
A) 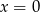 B)
B) 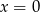 lub
lub 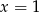 C)
C) 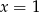 D)
D) 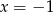
Liczby 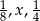 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 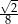 B)
B) 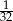 C)
C) 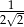 D)
D) 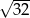
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 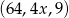 . Stąd wynika, że
. Stąd wynika, że
A) 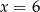 B)
B) 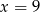 C)
C) 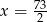 D)
D) 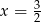
Jeżeli liczby 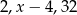 tworzą rosnący ciąg geometryczny, to
tworzą rosnący ciąg geometryczny, to
A) 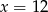 B)
B) 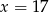 C)
C) 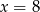 D)
D) 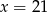
Liczby 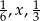 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 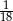 B)
B) 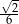 C)
C) 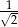 D)
D) 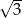
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 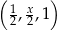 . Wówczas
. Wówczas
A) 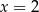 B)
B) 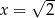 C)
C) 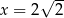 D)
D) 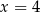
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 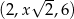 . Wówczas
. Wówczas
A) 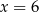 B)
B) 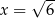 C)
C) 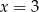 D)
D) 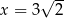
Trzywyrazowy ciąg 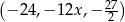 jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
A) 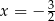 B)
B) 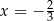 C)
C) 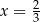 D)
D) 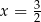
Liczby 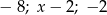 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  może być równa
może być równa
A) 4 B) 6 C) 7 D) 8
Trójwyrazowy ciąg 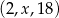 jest rosnącym ciągiem geometrycznym. Wtedy
jest rosnącym ciągiem geometrycznym. Wtedy
A) 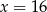 B)
B) 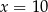 C)
C) 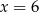 D)
D) 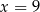
Trzywyrazowy ciąg 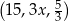 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 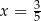 B)
B) 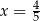 C)
C) 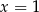 D)
D) 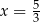
W rosnącym ciągu geometrycznym stosunek wyrazu czwartego do drugiego jest równy 8. Iloraz tego ciągu jest równy
A) 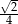 B) 4 C)
B) 4 C) 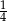 D)
D) 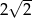
Dany jest ciąg geometryczny 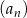 , określony dla
, określony dla 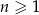 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 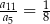 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 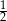 B)
B) 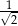 C)
C) 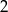 D)
D) 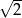
Dany jest ciąg geometryczny 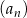 , określony dla
, określony dla 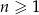 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 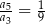 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 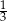 B)
B) 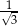 C) 3 D)
C) 3 D) 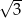
Suma
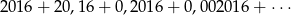
wszystkich wyrazów nieskończonego ciągu liczb rzeczywistych jest równa
A) 201600 B) 2240 C) 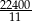 D)
D) 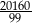
Suma
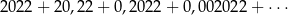
wszystkich wyrazów nieskończonego ciągu geometrycznego liczb rzeczywistych jest równa
A) 202200 B) 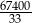 C) 67400 D)
C) 67400 D) 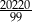
W ciągu geometrycznym 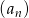 dane są
dane są 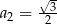 i
i 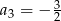 . Wtedy wyraz
. Wtedy wyraz 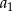 jest równy
jest równy
A) 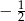 B)
B) 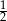 C)
C) 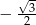 D)
D) 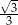
W ciągu geometrycznym 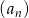 dane są
dane są 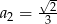 i
i 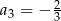 . Wtedy wyraz
. Wtedy wyraz 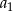 jest równy
jest równy
A) 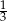 B)
B) 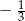 C)
C) 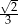 D)
D) 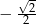
Dany jest ciąg geometryczny 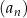 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 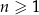 . Pierwszy wyraz tego ciągu jest równy 288, natomiast iloraz ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy 288, natomiast iloraz ciągu jest równy 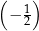 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wśród wyrazów ciągu 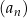 jest dokładnie 5 liczb całkowitych. jest dokładnie 5 liczb całkowitych. | P | F |
Jeden z wyrazów ciągu 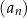 jest równy jest równy 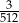 . . | P | F |
Dany jest ciąg geometryczny 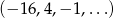 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 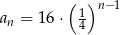 B)
B) 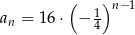 C)
C) 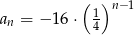 D)
D) 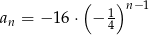
Dany jest ciąg geometryczny 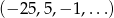 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 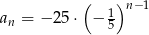 B)
B) 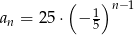 C)
C) 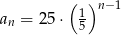 D)
D) 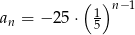
Dany jest ciąg geometryczny 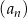 , określony dla
, określony dla 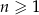 , w którym
, w którym 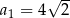 ,
, 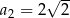 ,
, 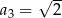 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 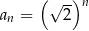 B)
B) 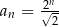 C)
C) 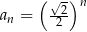 D)
D) 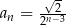
Dany jest ciąg geometryczny 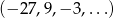 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 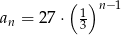 B)
B) 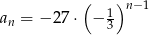 C)
C) 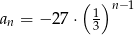 D)
D) 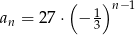
Dany jest ciąg geometryczny 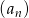 , określony dla
, określony dla 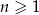 , w którym
, w którym 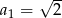 ,
, 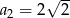 ,
, 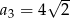 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 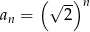 B)
B) 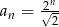 C)
C) 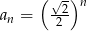 D)
D) 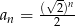
Nieskończony ciąg geometryczny 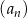 spełnia warunki:
spełnia warunki: 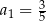 oraz
oraz 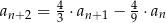 dla
dla 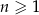 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A) 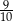 B)
B) 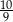 C)
C)  D)
D) 
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 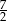 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 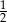 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 0,25 B) 1 C) -0,25 D) -1
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 39. Iloraz tego ciągu jest równy 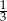 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 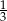 B) 1 C)
B) 1 C) 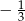 D) 3
D) 3
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 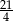 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 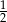 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 0,25 B) 0,75 C) 0,375 D) -0,75
Ile wyrazów ma ciąg geometryczny 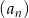 , w którym
, w którym 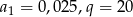 , natomiast ostatni wyraz jest równy 4000?
, natomiast ostatni wyraz jest równy 4000?
A) 3 B) 4 C) 5 D) 6
Ile wyrazów ma ciąg geometryczny 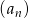 , w którym
, w którym 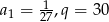 , natomiast ostatni wyraz jest równy 1000?
, natomiast ostatni wyraz jest równy 1000?
A) 3 B) 4 C) 5 D) 6
Ile wyrazów ma ciąg geometryczny 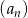 , w którym
, w którym 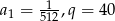 , natomiast ostatni wyraz jest równy 5000?
, natomiast ostatni wyraz jest równy 5000?
A) 3 B) 4 C) 5 D) 6
Pięciowyrazowy ciąg 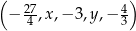 jest geometryczny i nie wszystkie jego wyrazy są ujemne. Iloczyn wszystkich wyrazów tego ciągu jest równy
jest geometryczny i nie wszystkie jego wyrazy są ujemne. Iloczyn wszystkich wyrazów tego ciągu jest równy
A) 81 B) 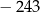 C)
C) 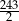 D)
D) 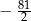
Dany jest ciąg geometryczny o wyrazie ogólnym 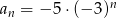 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) -135 B) -45 C) 45 D) 135
Dany jest ciąg geometryczny o wyrazie ogólnym 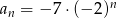 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) -28 B) 56 C) -56 D) 28
Dany jest ciąg geometryczny o wyrazie ogólnym 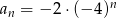 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) -128 B) -32 C) 128 D) 32

