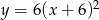Najmniejszą wartością funkcji kwadratowej 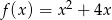 jest
jest
A) 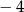 B)
B) 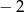 C) 0 D) 4
C) 0 D) 4
/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa
Najmniejszą wartością funkcji kwadratowej 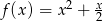 jest
jest
A) 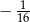 B)
B) 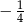 C)
C) 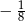 D)
D) 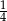
Wskaż postać kanoniczną trójmianu 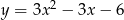 .
.
A) 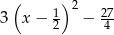 B)
B) 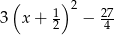 C)
C) 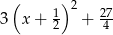 D)
D) 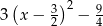
Prosta 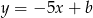 jest styczna do paraboli określonej wzorem
jest styczna do paraboli określonej wzorem 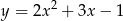 . Liczba
. Liczba 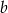 jest równa
jest równa
A) 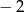 B) 1 C)
B) 1 C) 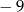 D) 11
D) 11
Największą wartością funkcji kwadratowej 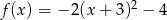 jest
jest
A) 3 B) -2 C) -4 D) 4
Największą wartością funkcji kwadratowej 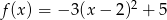 jest
jest
A) -3 B) 5 C) -5 D) 2
Funkcja kwadratowa 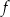 jest określona wzorem
jest określona wzorem 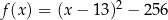 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 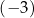 . Drugim miejscem zerowym funkcji
. Drugim miejscem zerowym funkcji 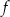 jest liczba
jest liczba
A) 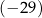 B)
B) 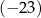 C) 23 D) 29
C) 23 D) 29
Funkcja kwadratowa 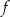 jest określona wzorem
jest określona wzorem 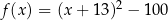 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 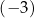 . Drugim miejscem zerowym funkcji
. Drugim miejscem zerowym funkcji 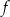 jest liczba
jest liczba
A) 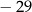 B)
B) 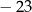 C) 23 D) 29
C) 23 D) 29
Funkcja 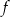 jest określona wzorem
jest określona wzorem 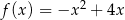 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 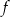 jest przedział
jest przedział
A) 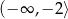 B)
B) 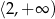 C)
C) 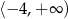 D)
D) 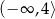
Funkcja 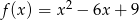 dla argumentu
dla argumentu 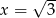 przyjmuje wartość
przyjmuje wartość
A) 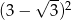 B) -36 C)
B) -36 C) 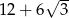 D)
D) 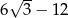
Funkcja 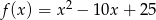 dla argumentu
dla argumentu 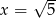 przyjmuje wartość
przyjmuje wartość
A) 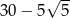 B) -20 C)
B) -20 C) 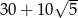 D)
D) 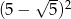
Funkcje 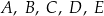 oraz
oraz 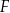 są określone dla każdej liczby rzeczywistej
są określone dla każdej liczby rzeczywistej  . Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Przedział ![(− ∞ ,2]](https://img.zadania.info/zad/5429286/HzadT3x.png) jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
A) 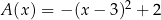 B)
B) 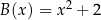 C)
C) 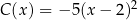
D) 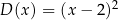 E)
E) 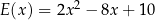 F)
F) 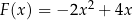
Funkcje 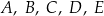 oraz
oraz  są określone dla każdej liczby rzeczywistej
są określone dla każdej liczby rzeczywistej  . Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Przedział 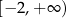 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
A) 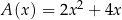 B)
B) 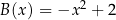 C)
C) 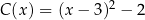
D) 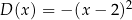 E)
E) 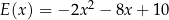 F)
F) 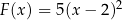
Wskaż funkcję kwadratową rosnąca w przedziale 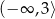 .
.
A) 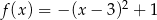 B)
B) 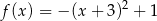
C) 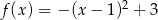 D)
D) 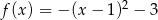
Wskaż funkcję kwadratową rosnąca w przedziale 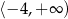 .
.
A) 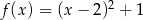 B)
B) 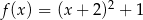
C) 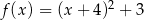 D)
D) 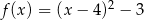
Wskaż funkcję kwadratową malejącą w przedziale 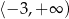 .
.
A) 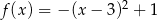 B)
B) 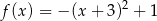
C) 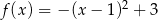 D)
D) 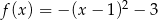
Dana jest funkcja kwadratowa 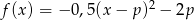 , gdzie
, gdzie 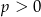 . Wówczas
. Wówczas
A) funkcja osiąga największą wartość równą 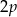 ;
;
B) funkcja ma dwa różne miejsca zerowe;
C) wierzchołek paraboli będącej wykresem 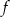 należy do prostej o równaniu
należy do prostej o równaniu 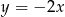 ;
;
D) dla 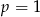 funkcja jest rosnąca w całej swojej dziedzinie.
funkcja jest rosnąca w całej swojej dziedzinie.
Funkcja kwadratowa określona jest wzorem 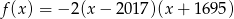 . Wynika stąd, że
. Wynika stąd, że
A) 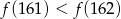 B)
B) 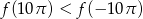 C)
C) 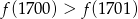 D)
D) 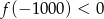
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę 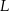 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
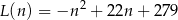
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 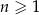 i
i 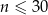 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa 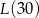 . . | P | F |
| W trzecim dniu analizowanego okresu obsłużono 336 klientów. | P | F |
Właściciel pewnej piekarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 28 kolejnych dni. Przyjmijmy, że liczbę 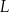 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
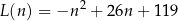
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 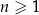 i
i 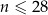 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W piątym dniu analizowanego okresu obsłużono 224 klientów. | P | F |
Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa 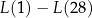 . . | P | F |
Jeśli funkcja kwadratowa 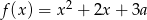 nie ma ani jednego miejsca zerowego, to liczba
nie ma ani jednego miejsca zerowego, to liczba  spełnia warunek
spełnia warunek
A) 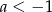 B)
B) 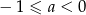 C)
C) 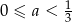 D)
D) 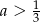
Jeśli funkcja kwadratowa 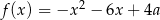 ma dwa miejsca zerowe, to liczba
ma dwa miejsca zerowe, to liczba  spełnia warunek
spełnia warunek
A) 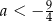 B)
B) 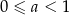 C)
C) 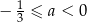 D)
D) 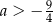
Jeśli funkcja kwadratowa 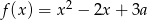 ma dwa miejsca zerowe, to liczba
ma dwa miejsca zerowe, to liczba  spełnia warunek
spełnia warunek
A) 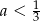 B)
B) 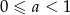 C)
C) 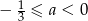 D)
D) 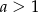
Jeśli funkcja kwadratowa 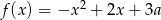 nie ma ani jednego miejsca zerowego, to liczba
nie ma ani jednego miejsca zerowego, to liczba  spełnia warunek
spełnia warunek
A) 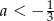 B)
B) 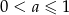 C)
C) 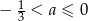 D)
D) 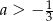
Funkcja 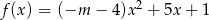 osiąga wartość największą dla
osiąga wartość największą dla
A) 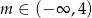 B)
B) 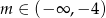 C)
C) 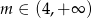 D)
D) 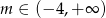
Funkcja kwadratowa 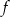 określona wzorem
określona wzorem 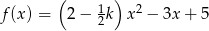 osiąga wartość największą, gdy
osiąga wartość największą, gdy
A) 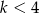 B)
B) 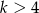 C)
C) 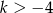 D)
D) 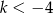
Funkcja kwadratowa 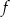 określona wzorem
określona wzorem 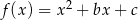 osiąga dla
osiąga dla 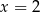 wartość najmniejszą równą 4. Wtedy
wartość najmniejszą równą 4. Wtedy
A) 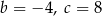 B)
B) 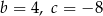
C) 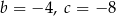 D)
D) 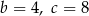
Funkcja 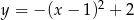 jest rosnąca w przedziale:
jest rosnąca w przedziale:
A) 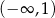 B)
B) 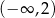 C)
C) 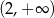 D)
D) 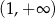
Funkcja kwadratowa 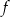 określona wzorem
określona wzorem 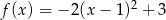 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 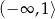 B)
B) 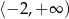 C)
C) 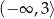 D)
D) 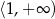
Funkcja 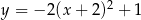 jest rosnąca w przedziale:
jest rosnąca w przedziale:
A) 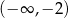 B)
B) 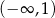 C)
C) 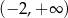 D)
D) 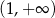
Największą wartość równą 5 funkcja kwadratowa przyjmuje dla argumentu równego 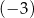 . Ten warunek spełnia funkcja o równaniu:
. Ten warunek spełnia funkcja o równaniu:
A) 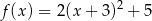 B)
B) 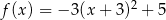
C) 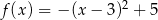 D)
D) 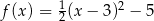
Funkcja kwadratowa 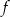 przyjmuje wartość największą równą
przyjmuje wartość największą równą 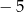 dla argumentu równego 2. Ten warunek spełnia funkcja o równaniu:
dla argumentu równego 2. Ten warunek spełnia funkcja o równaniu:
A) 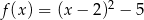 B)
B) 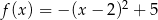
C) 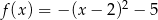 D)
D) 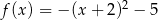
Zbiorem wartości funkcji 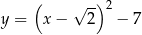 określonej w przedziale
określonej w przedziale 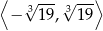 jest
jest
A) 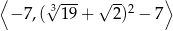 B)
B) 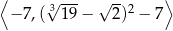
C) 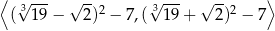 D)
D) 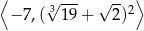
Właściciel pewnej pączkarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 40 kolejnych dni. Przyjmijmy, że liczbę 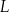 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
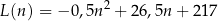
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 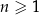 i
i 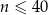 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W jednym z dni poddanych analizie, liczba klientów obsłużonych w pączkarni była równa 448. | P | F |
| W 19 dniu analizowanego okresu obsłużono tyle samo klientów, ile obsłużono w dniu 34. | P | F |
Wskaż funkcję, która w przedziale 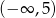 jest malejąca.
jest malejąca.
A) 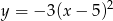 B)
B) 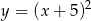 C)
C) 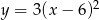 D)
D) 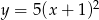
Wskaż funkcję, która w przedziale 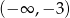 jest malejąca.
jest malejąca.
A) 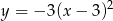 B)
B) 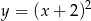 C)
C) 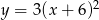 D)
D)