Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 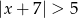 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 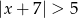 .
.

Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 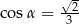 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 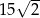 B) 45 C)
B) 45 C) 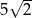 D) 10
D) 10
Oblicz, ile jest liczb naturalnych ośmiocyfrowych takich, że iloczyn cyfr w ich zapisie dziesiętnym jest równy 12.
W pewnym banku prowizja od udzielanych kredytów hipotecznych przez cały styczeń była równa 4%. Na początku lutego ten bank obniżył wysokość prowizji od wszystkich kredytów o 1 punkt procentowy. Oznacza to, że prowizja od kredytów hipotecznych w tym banku zmniejszyła się o
A) 1% B) 25% C) 33% D) 75%
Rozwiąż nierówność 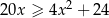 .
.
Prosta przechodząca przez punkty 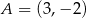 i
i 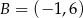 jest określona równaniem
jest określona równaniem
A) 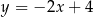 B)
B) 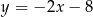 C)
C) 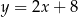 D)
D) 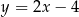
Ciąg geometryczny 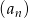 jest określony wzorem
jest określony wzorem 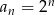 dla
dla 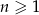 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 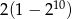 B)
B) 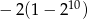 C)
C) 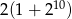 D)
D) 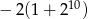
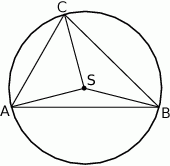
Punkt 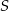 jest środkiem okręgu opisanego na trójkącie ostrokątnym
jest środkiem okręgu opisanego na trójkącie ostrokątnym 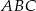 . Kąt
. Kąt 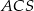 jest trzy razy większy od kąta
jest trzy razy większy od kąta 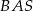 , a kąt
, a kąt 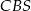 jest dwa razy większy od kąta
jest dwa razy większy od kąta 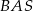 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 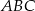 .
.
Trapez równoramienny 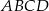 o podstawach
o podstawach 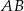 i
i 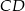 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 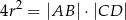 .
.
Średnia wieku w pewnej grupie studentów jest równa 23 lata. Średnia wieku tych studentów i ich opiekuna jest równa 24 lata. Opiekun ma 39 lat. Oblicz, ilu studentów jest w tej grupie.
Bok rombu ma taką samą długość jak przekątna kwadratu. Pole rombu jest równe polu kwadratu. Zatem kąt ostry tego rombu ma miarę
A) 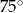 B)
B) 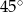 C)
C) 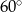 D)
D) 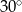
Bok 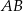 czworokąta
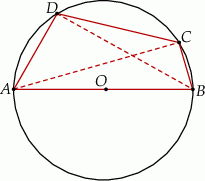
czworokąta 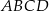 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 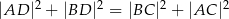 .
.
W pudełku jest 8 kul, z czego 5 białych i 3 czarne. Do tego pudełka dołożono  kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe
kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe 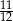 . Oblicz
. Oblicz  .
.
Wyznacz wszystkie wartości parametru 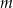 , dla których równanie
, dla których równanie
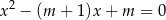
ma dwa różne rozwiązania rzeczywiste 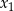 oraz
oraz 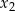 , spełniające warunki:
, spełniające warunki:
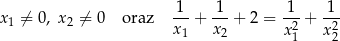
Dany jest nieskończony rosnący ciąg arytmetyczny 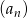 , dla
, dla 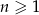 taki, że
taki, że 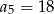 . Wyrazy
. Wyrazy 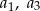 oraz
oraz 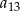 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 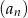 .
.
Dane są wektory ![→ u = [4,− 5]](https://img.zadania.info/zad/9621448/HzadT0x.gif) oraz
oraz ![→ v = [− 1,− 5]](https://img.zadania.info/zad/9621448/HzadT1x.gif) . Długość wektora
. Długość wektora 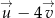 jest równa
jest równa
A) 7 B) 15 C) 17 D) 23
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
A) 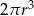 B)
B) 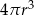 C)
C) 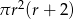 D)
D) 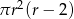
Pusta bańka na mleko o pojemności 10 litrów ma masę 6,5 kg. Jeden litr mleka ma masę 1,03 kg. Niech  oznacza liczbę litrów mleka w tej bańce, a
oznacza liczbę litrów mleka w tej bańce, a 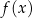 oznacza wyrażoną w kilogramach masę bańki wraz z mlekiem, gdzie
oznacza wyrażoną w kilogramach masę bańki wraz z mlekiem, gdzie ![x ∈ [0,1 0]](https://img.zadania.info/zad/9628036/HzadT2x.png) . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 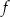 jest malejąca. jest malejąca. | P | F |
Funkcja 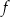 nie ma miejsc zerowych. nie ma miejsc zerowych. | P | F |
Niech 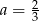 ,
, 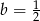 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 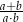 jest równa
jest równa
A) 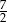 B)
B) 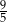 C)
C) 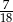 D)
D) 
Rozwiąż równanie 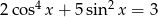 w przedziale
w przedziale 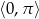 .
.
