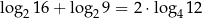W pudełku jest 50 kuponów, wśród których jest 15 kuponów przegrywających, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 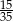 B)
B) 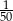 C)
C) 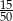 D)
D) 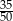
/Szkoła średnia
Pierwsza współrzędna wierzchołka paraboli o równaniu 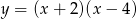 jest równa
jest równa
A) 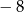 B)
B) 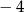 C) 1 D) 2
C) 1 D) 2
Funkcja kwadratowa 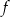 określona wzorem
określona wzorem 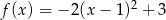 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 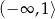 B)
B) 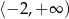 C)
C) 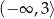 D)
D) 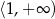
Punkt 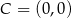 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 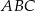 , którego wierzchołek
, którego wierzchołek 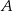 leży na osi
leży na osi 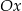 , a wierzchołek
, a wierzchołek 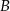 na osi
na osi 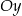 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 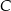 przecina przeciwprostokątną
przecina przeciwprostokątną 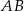 w punkcie
w punkcie 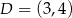 .
.
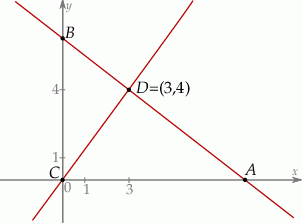
Oblicz współrzędne wierzchołków 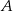 i
i 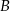 tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej 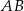 .
.
W układzie współrzędnych narysuj okrąg o równaniu 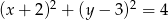 oraz zaznacz punkt
oraz zaznacz punkt 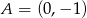 . Prosta o równaniu
. Prosta o równaniu 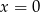 jest jedną ze stycznych do tego okręgu przechodzących przez punkt
jest jedną ze stycznych do tego okręgu przechodzących przez punkt 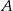 . Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt
. Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt 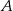 .
.
W układzie współrzędnych dane są punkty 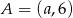 oraz
oraz 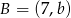 . Środkiem odcinka
. Środkiem odcinka 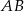 jest punkt
jest punkt 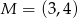 . Wynika stąd, że
. Wynika stąd, że
A) 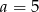 i
i 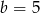 B)
B) 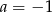 i
i 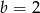 C)
C) 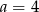 i
i 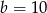 D)
D) 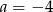 i
i 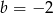
W ciągu arytmetycznym 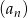 , dla
, dla 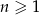 , dane są
, dane są 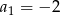 oraz różnica
oraz różnica 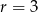 . Oblicz największe
. Oblicz największe  takie, że
takie, że 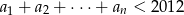 .
.
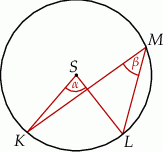
Dany jest okrąg o środku 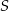 . Punkty
. Punkty 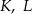 i
i 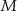 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 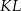 tego okręgu są oparte kąty
tego okręgu są oparte kąty 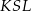 i
i 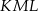 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 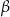 spełniają warunek
spełniają warunek 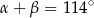 . Wynika stąd, że
. Wynika stąd, że
A) 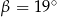 B)
B) 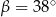 C)
C) 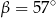 D)
D) 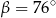
Oblicz, ile jest liczb naturalnych sześciocyfrowych, w zapisie których występuje dokładnie trzy razy cyfra 0 i dokładnie raz występuje cyfra 5.
Ciąg 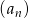 jest określony wzorem
jest określony wzorem
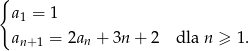
Oblicz średnią arytmetyczną liczb 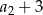 i
i 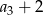 .
.
Na diagramie przedstawiono wyniki sprawdzianu z matematyki w pewnej klasie maturalnej. Na osi poziomej podano oceny, które uzyskali uczniowie tej klasy, a na osi pionowej podano liczbę uczniów, którzy otrzymali daną ocenę.
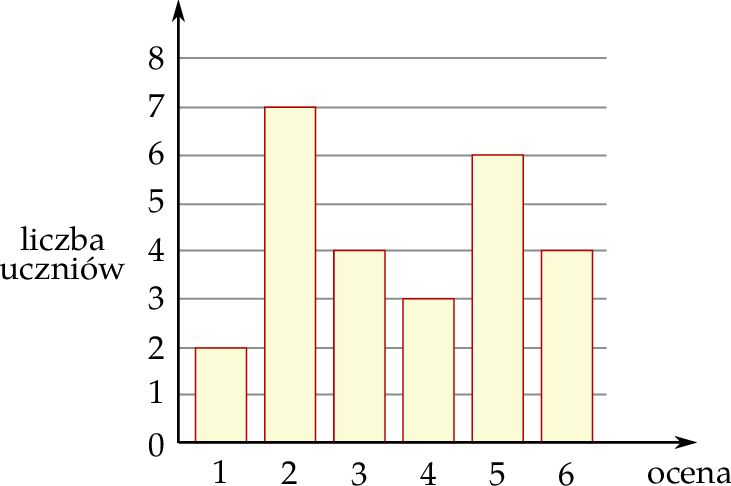
Mediana ocen uzyskanych z tego sprawdzianu przez uczniów tej klasy jest równa
A) 4,5 B) 4 C) 3,5 D) 3
Rozwiąż równanie 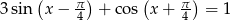 w przedziale
w przedziale 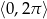 .
.
Miasta 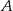 i
i 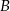 są odległe o 450 km. Pani Danuta pokonała tę trasę swym samochodem w czasie o 75 minut dłuższym niż pani Lidia. Wartość średniej prędkości, z jaką jechała pani Danuta na całej trasie, była o 18 km/h mniejsza od wartości średniej prędkości, z jaką jechała pani Lidia. Oblicz średnie wartości:
są odległe o 450 km. Pani Danuta pokonała tę trasę swym samochodem w czasie o 75 minut dłuższym niż pani Lidia. Wartość średniej prędkości, z jaką jechała pani Danuta na całej trasie, była o 18 km/h mniejsza od wartości średniej prędkości, z jaką jechała pani Lidia. Oblicz średnie wartości:
– prędkości, z jaką pani Danuta jechała z A do B.
– prędkości, z jaką pani Lidia jechała z A do B.
Rozwiązaniem równania 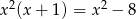 jest
jest
A) 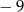 B)
B) 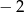 C) 2 D) 7
C) 2 D) 7
Kąt  jest taki, że
jest taki, że 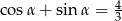 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 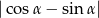 .
.
Największą liczbą będącą rozwiązaniem rzeczywistym równania 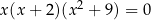 jest
jest
A) 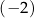 B) 0 C) 2 D) 3
B) 0 C) 2 D) 3
Ciąg 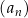 jest określony wzorem
jest określony wzorem 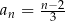 dla każdej liczby naturalnej
dla każdej liczby naturalnej 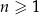 . Liczba wyrazów tego ciągu mniejszych od 10 jest równa
. Liczba wyrazów tego ciągu mniejszych od 10 jest równa
A) 28 B) 31 C) 32 D) 27
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są jedna kula biała i sześć kul czarnych, w drugiej urnie są cztery kule białe i trzy kule czarne. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy kulę białą w tym doświadczeniu, jest równe
A) 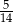 B)
B) 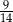 C)
C)  D)
D) 
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 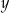 takich, że
takich, że 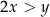 , spełniona jest nierówność
, spełniona jest nierówność
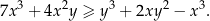
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Prawdziwe są równości
A) 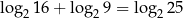 B)
B) 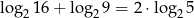
C) 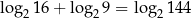 D)
D) 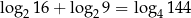
E) 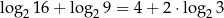 F)
F)