Osią symetrii wykresu funkcji kwadratowej 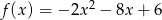 jest prosta o równaniu
jest prosta o równaniu
A) 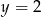 B)
B) 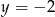 C)
C) 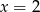 D)
D) 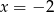
/Szkoła średnia
Trzywyrazowy ciąg 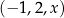 jest arytmetyczny. Trzywyrazowy ciąg
jest arytmetyczny. Trzywyrazowy ciąg 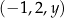 jest geometryczny. Liczby
jest geometryczny. Liczby  oraz
oraz 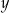 spełniają warunki
spełniają warunki
A) 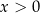 i
i 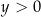 B)
B) 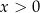 i
i 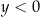 C)
C) 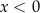 i
i 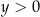 D)
D) 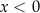 i
i 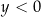
Liczba 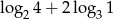 jest równa
jest równa
A) 0 B) 1 C) 2 D) 4
Kąt  jest ostry i
jest ostry i 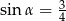 . Wartość wyrażenia
. Wartość wyrażenia 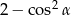 jest równa
jest równa
A) 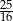 B)
B)  C)
C) 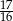 D)
D) 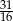
Buty, które kosztowały 220 złotych, przeceniono i sprzedano za 176 złotych. O ile procent obniżono cenę butów?
A) 80 B) 20 C) 22 D) 44
Liczby 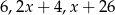 w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę
w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę  tego ciągu.
tego ciągu.
Miejsce zerowe funkcji liniowej 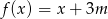 jest większe od 2 dla każdej liczby
jest większe od 2 dla każdej liczby 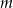 spełniającej warunek
spełniającej warunek
A) 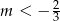 B)
B) 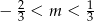 C)
C) 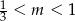 D)
D) 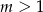
Ze zbioru 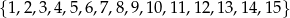 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 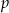 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
A) 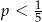 B)
B) 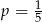 C)
C) 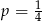 D)
D) 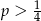
Rozwiąż równanie 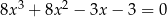 .
.
Liczba 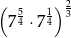 jest równa
jest równa
A) 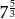 B)
B) 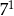 C)
C) 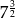 D)
D) 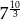
Liczba 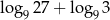 jest równa
jest równa
A) 81 B) 9 C) 4 D) 2
Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 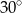 i
i 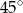 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
Dany jest prostopadłościan 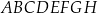 , w którym podstawy
, w którym podstawy 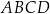 i
i 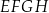 są kwadratami o boku długości 6. Przekątna
są kwadratami o boku długości 6. Przekątna 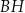 tego prostopadłościanu tworzy z przekątną
tego prostopadłościanu tworzy z przekątną 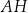 ściany bocznej
ściany bocznej 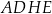 kąt o mierze
kąt o mierze 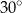 (zobacz rysunek).
(zobacz rysunek).
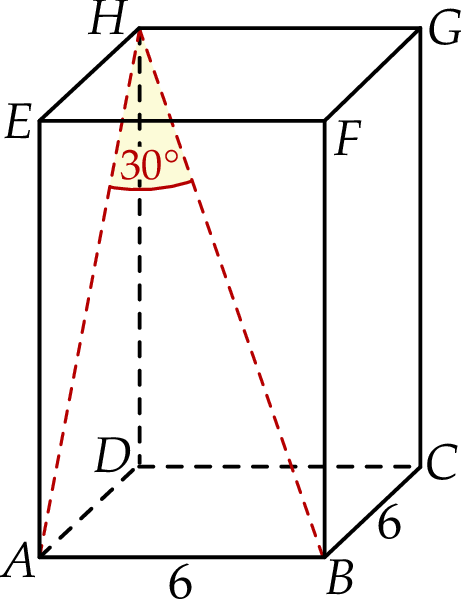
Przekątna 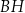 tego prostopadłościanu ma długość równą
tego prostopadłościanu ma długość równą
A) 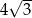 B)
B) 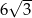 C) 12 D)
C) 12 D) 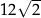
Pierwszy wyraz ciągu geometrycznego jest równy 8, a czwarty wyraz tego ciągu jest równy 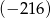 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 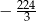 B)
B) 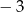 C)
C) 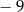 D)
D) 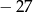
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 15, jeśli wiadomo, że jest ona podzielna przez 18.
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 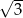 . Zatem
. Zatem
A) 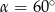 B)
B) 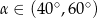 C)
C) 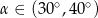 D)
D) 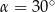
Suma 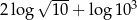 jest równa
jest równa
A) 2 B) 3 C) 4 D) 5
Okrąg 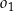 o środku w punkcie
o środku w punkcie 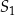 jest określony równaniem
jest określony równaniem 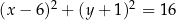 . Okrąg
. Okrąg 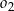 ma środek w punkcie
ma środek w punkcie 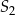 takim, że
takim, że ![−→ S 1S2 = [− 4,4]](https://img.zadania.info/zad/9553446/HzadT5x.png) . Promienie tych okręgów są sobie równe. Figura
. Promienie tych okręgów są sobie równe. Figura 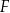 składa się z dwóch okręgów:
składa się z dwóch okręgów: 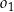 oraz
oraz 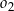 . Punkty
. Punkty 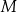 i
i 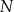 są punktami przecięcia figury
są punktami przecięcia figury 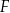 z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt
z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt 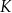 , leżący na jednej z osi symetrii figury
, leżący na jednej z osi symetrii figury 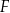 , taki, że pole trójkąta
, taki, że pole trójkąta 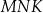 jest równe 40.
jest równe 40.
W trójkącie 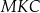 bok
bok 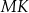 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 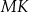 przecina boki
przecina boki 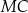 i
i 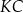 – odpowiednio – w punktach
– odpowiednio – w punktach 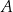 oraz
oraz 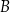 takich, że
takich, że 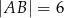 i
i 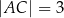 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 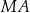 jest równa
jest równa
A) 18 B) 15 C) 9 D) 12

