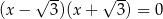Liczba 3 jest rozwiązaniem równania
A) 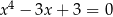 B)
B) 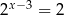 C)
C) 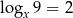 D)
D) 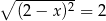
/Szkoła średnia/Zadania testowe/Równania/Różne
Suma rozwiązań równania 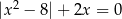 jest równa
jest równa
A) 0 B) 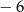 C) 2 D)
C) 2 D) 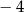
Para liczb 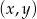 , która spełnia równanie
, która spełnia równanie 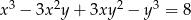 to
to
A) 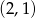 B)
B) 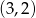 C)
C) 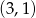 D)
D) 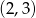
Rozwiązaniem równania 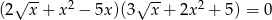 jest liczba
jest liczba
A) 1 B) 2 C) 4 D) 9
Zbiór rozwiązań równania 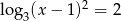 jest taki sam, jak zbiór rozwiązań równania:
jest taki sam, jak zbiór rozwiązań równania:
A) 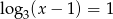 B)
B) 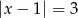 C)
C) 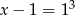 D)
D) 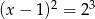
Zbiór rozwiązań równania 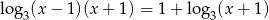 jest taki sam, jak zbiór rozwiązań równania:
jest taki sam, jak zbiór rozwiązań równania:
A) 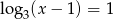 B)
B) 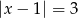 C)
C) 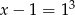 D)
D) 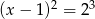
Wspólnym pierwiastkiem równań 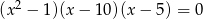 oraz
oraz 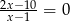 jest liczba
jest liczba
A) 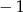 B) 1 C) 5 D) 10
B) 1 C) 5 D) 10
Wspólnym pierwiastkiem równań 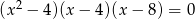 oraz
oraz 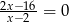 jest liczba
jest liczba
A) 2 B) 4 C) 8 D) 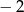
Wspólnym pierwiastkiem równań 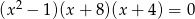 oraz
oraz 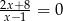 jest liczba
jest liczba
A) 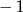 B) 1 C)
B) 1 C) 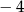 D)
D) 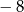
Które z podanych równań nie ma rozwiązania:
A) 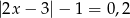 B)
B) 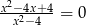 C)
C) 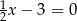 D)
D) 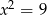
Jeśli 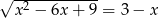 , to liczba
, to liczba  może być równa
może być równa
A) 10 B) 1 C) 4 D) 3,5
Jeśli 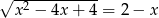 , to liczba
, to liczba  może być równa
może być równa
A) 3 B) 5 C) 4 D) -1
Jeśli 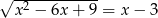 , to liczba
, to liczba  może być równa
może być równa
A) 10 B) 1 C) -4 D) 0
Liczba 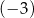 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 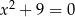 B)
B) 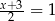 C)
C) 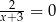 D)
D) 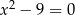
Liczba 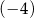 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 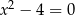 B)
B) 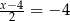 C)
C) 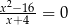 D)
D) 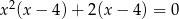
Liczba 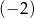 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 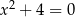 B)
B) 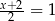 C)
C) 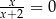 D)
D) 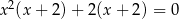
Równanie 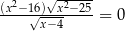 ma dokładnie
ma dokładnie
A) cztery rozwiązania B) trzy rozwiązania
C) dwa rozwiązania D) jedno rozwiązanie
Rozwiązaniem równania 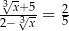 jest liczba
jest liczba
A) 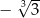 B)
B) 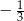 C)
C) 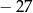 D)
D) 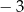
Równanie 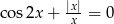 w zbiorze
w zbiorze 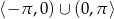
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Jaką liczbę należy podstawić zamiast litery  , aby równanie
, aby równanie 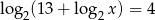 było prawdziwe?
było prawdziwe?
A) 8 B) 12 C) 16 D) 32
Wskaż parę równań równoważnych
A) 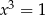 i
i 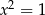 B)
B) 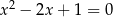 i
i 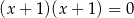
C) 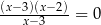 i
i 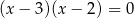 D)
D) 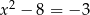 i
i 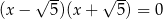
Równania równoważne to
A) 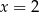 i
i 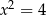 B)
B) 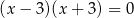 i
i 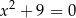
C) 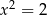 i
i 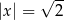 D)
D) 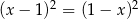 i
i 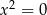
Wskaż parę równań równoważnych
A) 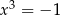 i
i 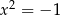 B)
B) 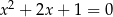 i
i 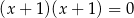
C) 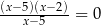 i
i 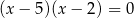 D)
D) 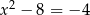 i
i 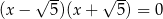
Wskaż parę równań równoważnych
A) 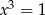 i
i 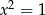 B)
B) 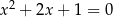 i
i 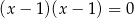
C) 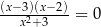 i
i 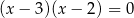 D)
D) 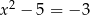 i
i