Pan Jakub ma 4 marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 21 C) 28 D) 70
/Szkoła średnia/Zadania testowe/Kombinatoryka/Różne
Pan Jakub ma 8 marynarek, 5 par różnych spodni i 9 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 240 B) 22 C) 360 D) 90
Andrzej ma w szafie 4 koszule: czerwoną, żółtą, zieloną i niebieską; 3 pary spodni: niebieskie, czarne i szare; oraz 5 par butów: czarne, szare, zielone, czerwone i niebieskie. Andrzej wybiera z szafy zestaw ubrania: jedną koszulę, jedną parę spodni i jedną parę butów. Zestawy ubrania wybierane przez Andrzeja określimy jako różne, gdy będą różniły się kolorem chociaż jednego rodzaju elementu ubioru w zestawie. Liczba wszystkich możliwych, różnych zestawów ubrania, jakie może wybrać Andrzej, jest równa
A) 12 B) 72 C) 60 D) 720
Pan Łukasz ma 3 marynarki, 8 par różnych spodni i 11 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 22 C) 132 D) 264
Pan Tomasz ma 5 marynarek, 9 par różnych spodni i 6 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 20 B) 45 C) 280 D) 270
Wyrażenie 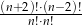 dla liczby naturalnej
dla liczby naturalnej 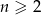 jest równe
jest równe
A) 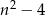 B)
B) 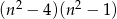 C)
C) 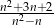 D)
D) 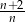
Wyrażenie 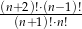 dla liczby naturalnej
dla liczby naturalnej 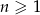 jest równe
jest równe
A) 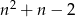 B)
B) 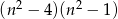 C)
C) 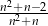 D)
D) 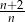
Ile różnych wyrazów z sensem lub bez sensu można ułożyć z liter wyrazu: MATEMATYKA?
A) 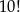 B) 30240 C) 151200 D)
B) 30240 C) 151200 D) 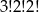
Pan Eugeniusz szykując się rano do pracy wybiera jeden spośród swoich 12 zegarków oraz dwa spośród 22 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 2777 B) 34 C) 5544 D) 5808
Pan Henryk szykując się rano do pracy wybiera jeden spośród swoich 10 zegarków oraz dwa spośród 18 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 45 B) 46 C) 3240 D) 3060
W pewnym mieście na czas festynu postanowiono rozstawić stragany. Ustalono, że będzie można ustawić po 3 stragany po każdej stronie drogi. Na ile sposobów można ustawić te stragany?
A) 6 B) 24 C) 36 D) 720
W trakcie zawodów sportowych ośmioro uczniów miało ustawić się w dwóch rzędach po 4 osoby. Na ile sposobów mogą ustawić się ci uczniowie?
A) 4 B) 576 C) 40320 D) 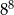
Liczba 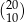 jest podzielna przez
jest podzielna przez
A) 5 B) 33 C) 221 D) 51
Liczba 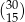 jest podzielna przez
jest podzielna przez
A) 7 B) 55 C) 143 D) 85
Na ile sposobów można ustawić na półce 5 tomów encyklopedii tak, aby tomy 3 i 4 stały obok siebie (w dowolnej kolejności)?
A) 24 B) 48 C) 120 D) 60
Na ile sposobów można ustawić na półce 6 tomów encyklopedii tak, aby tomy 4, 5 i 6 stały obok siebie (w dowolnej kolejności)?
A) 144 B) 48 C) 72 D) 24
Na regale można ustawić  książek na 24 sposoby. Zatem
książek na 24 sposoby. Zatem
A) 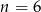 B)
B) 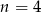 C)
C) 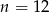 D)
D) 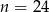
W kolejce do sklepu  osób można ustawić na 24 sposoby. Zatem
osób można ustawić na 24 sposoby. Zatem
A) 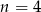 B)
B) 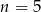 C)
C) 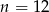 D)
D) 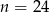
Na regale można ustawić  książek na 120 sposoby. Zatem
książek na 120 sposoby. Zatem
A) 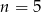 B)
B) 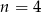 C)
C) 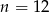 D)
D) 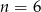
W karcie dań jest 5 zup i 4 drugie dania. Na ile sposobów można zamówić obiad składający się z jednej zupy i jednego drugiego dania?
A) 25 B) 20 C) 16 D) 9
W karcie dań są 4 zupy i 6 drugich dań. Na ile sposobów można zamówić obiad składający się z jednej zupy i jednego drugiego dania?
A) 24 B) 10 C) 16 D) 30
Wyrażenie 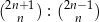 dla liczby naturalnej
dla liczby naturalnej 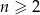 jest równe
jest równe
A) 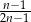 B)
B) 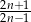 C) 2 D)
C) 2 D) 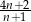
Na pierwszym polu 64-polowej szachownicy kładziemy jedno ziarnko maku, na drugim dwa ziarnka maku, na trzecim dwa razy więcej niż na drugim, na czwartym dwa razy więcej niż na trzecim itd. Ile ziarenek maku położymy w sumie na szachownicy?
A) 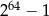 B)
B) 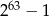 C)
C) 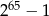 D)
D) 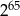
Ile różnych kodów czteroliterowych można utworzyć, przestawiając litery wyrazu MATA ?
A) 24 B) 12 C) 10 D) 8
Ile różnych kodów czteroliterowych można utworzyć, przestawiając litery wyrazu MODA?
A) 24 B) 12 C) 10 D) 8
Ile różnych kodów pięcioliterowych można utworzyć, przestawiając litery wyrazu ARABA?
A) 24 B) 12 C) 10 D) 20
Zamawiając pizzę mamy do wyboru 12 dodatków, 2 rodzaje ciasta i 3 rodzaje sosów. Na ile sposobów możemy zamówić pizzę jeżeli zdecydowaliśmy się wybrać jeden dodatek główny i jeden dodatek pomocniczy (różny od głównego), oraz jeden sos?
A) 28 B) 792 C) 29 D) 864

