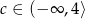Jednym z pierwiastków równania 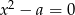 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 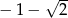 . Zatem liczba
. Zatem liczba  jest równa:
jest równa:
A) 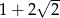 B)
B) 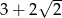 C)
C) 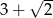 D) 0
D) 0
/Szkoła średnia/Zadania testowe/Równania/Kwadratowe/Z parametrem
Liczba 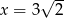 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 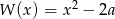 , gdy
, gdy  jest równe
jest równe
A) 18 B) 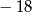 C) 9 D)
C) 9 D) 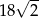
Jednym z pierwiastków równania 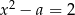 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 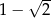 . Zatem drugim pierwiastkiem tego równania jest liczba:
. Zatem drugim pierwiastkiem tego równania jest liczba:
A) 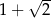 B)
B) 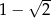 C)
C) 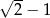 D) 0
D) 0
Jednym z miejsc zerowych funkcji kwadratowej 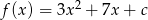 jest liczba
jest liczba 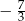 . Wówczas
. Wówczas  jest równe
jest równe
A) 0 B) 1 C) 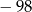 D) 98
D) 98
Jednym z miejsc zerowych funkcji kwadratowej 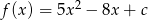 jest liczba
jest liczba  . Wówczas
. Wówczas  jest równe
jest równe
A) 1 B) 0 C) 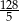 D)
D) 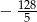
Jednym z pierwiastków równania 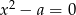 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 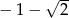 . Zatem drugim pierwiastkiem tego równania jest liczba:
. Zatem drugim pierwiastkiem tego równania jest liczba:
A) 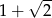 B)
B) 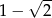 C)
C) 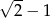 D)
D) 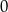
Funkcja 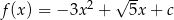 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 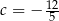 B)
B) 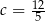 C)
C) 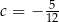 D)
D) 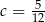
Równanie 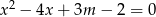 dokładnie jedno rozwiązanie gdy
dokładnie jedno rozwiązanie gdy
A) 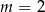 B)
B) 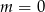 C)
C) 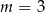 D)
D) 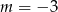
Funkcja kwadratowa 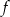 określona wzorem
określona wzorem 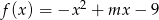 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 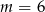 B)
B) 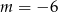 C)
C) 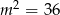 D)
D) 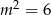
Pierwiastkami trójmianu kwadratowego 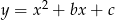 są liczby -4 i 6. Wynika stąd, że
są liczby -4 i 6. Wynika stąd, że
A) 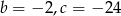 B)
B) 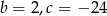 C)
C) 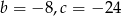 D)
D) 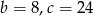
Pierwiastkami trójmianu kwadratowego 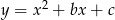 są liczby 4 i -6. Wynika stąd, że
są liczby 4 i -6. Wynika stąd, że
A) 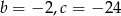 B)
B) 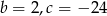 C)
C) 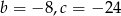 D)
D) 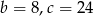
Pierwiastkami trójmianu kwadratowego 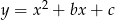 są liczby -2 i 3. Wynika stąd, że
są liczby -2 i 3. Wynika stąd, że
A) 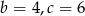 B)
B) 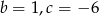 C)
C) 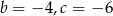 D)
D) 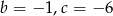
Dana jest funkcja 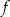 określona wzorem
określona wzorem 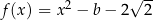 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 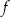 jest
jest 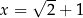 . Współczynnik
. Współczynnik 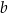 we wzorze funkcji
we wzorze funkcji 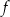 jest równy
jest równy
A) 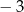 B) 3 C)
B) 3 C) 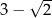 D)
D) 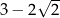
Suma szóstych potęg pierwiastków całkowitych równania 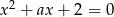 może być równa
może być równa
A) 65 B) 33 C) 2 D) 9
Funkcja kwadratowa 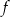 jest określona wzorem
jest określona wzorem 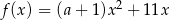 , gdzie
, gdzie  to pewna liczba rzeczywista. Liczba
to pewna liczba rzeczywista. Liczba 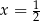 jest miejscem zerowym tej funkcji. Stąd wynika, że
jest miejscem zerowym tej funkcji. Stąd wynika, że
A) 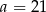 B)
B) 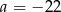 C)
C) 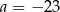 D)
D) 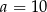
Miejscami zerowymi funkcji kwadratowej 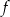 są liczby
są liczby 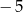 i 6, a miejscami zerowymi funkcji
i 6, a miejscami zerowymi funkcji 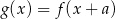 są liczby 1 i 12. Wynika stąd, że
są liczby 1 i 12. Wynika stąd, że
A) 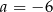 B)
B) 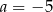 C)
C) 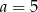 D)
D) 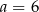
Równanie 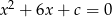 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 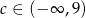 B)
B) 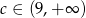 C)
C) 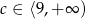 D)
D) 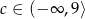
Równanie 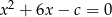 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 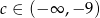 B)
B) 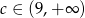 C)
C) 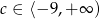 D)
D) 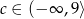
Równanie 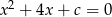 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 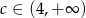 B)
B) 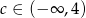 C)
C) 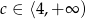 D)
D)