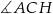W graniastosłupie prawidłowym sześciokątnym 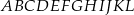 wierzchołki
wierzchołki 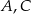 i
i 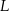 połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
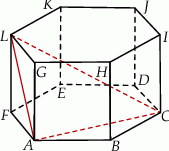
Cosinus największego kąta trójkąta 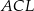 jest równy
jest równy
A)  B)
B) 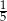 C) 0 D)
C) 0 D) 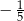
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W graniastosłupie prawidłowym sześciokątnym 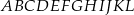 wierzchołki
wierzchołki 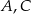 i
i 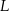 połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.

Cosinus największego kąta trójkąta 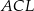 jest równy
jest równy
A)  B)
B) 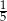 C) 0 D)
C) 0 D) 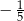
Kąt nachylenia najdłuższej przekątnej graniastosłupa prawidłowego sześciokątnego do płaszczyzny podstawy jest zaznaczony na rysunku
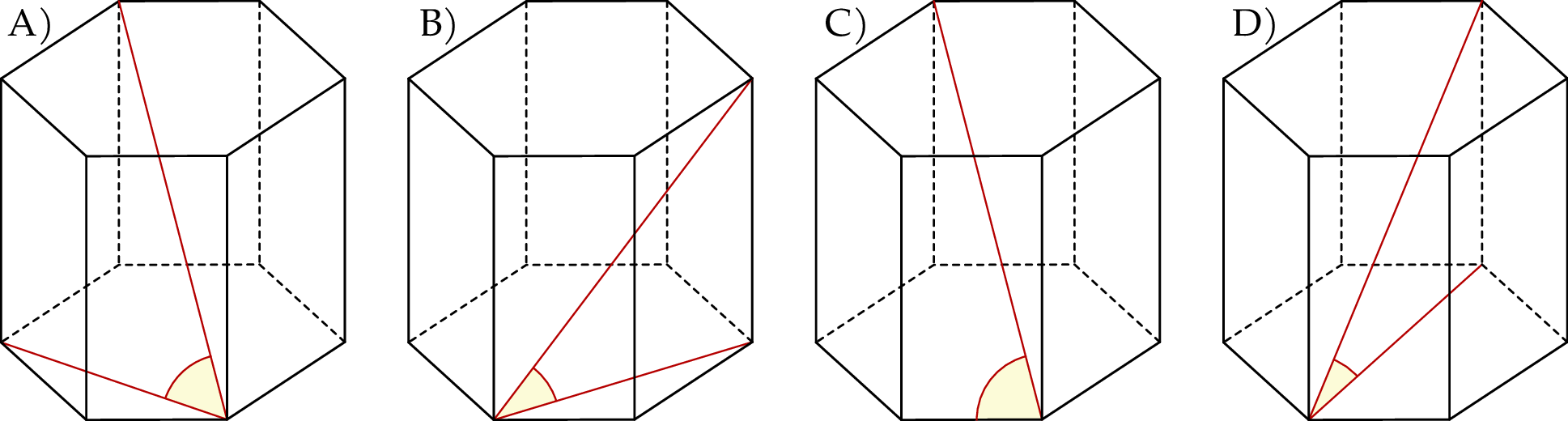
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2 (zobacz rysunek).
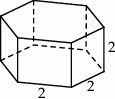
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 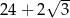 B)
B) 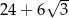 C)
C) 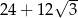 D)
D) 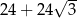
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 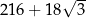 B)
B) 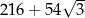 C)
C) 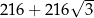 D)
D) 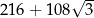
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 3 (zobacz rysunek).
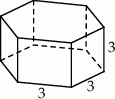
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 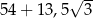 B)
B) 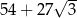 C)
C) 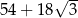 D)
D) 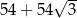
Dany jest graniastosłup prawidłowy sześciokątny 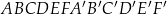 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 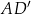 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 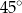 (zobacz rysunek).
(zobacz rysunek).
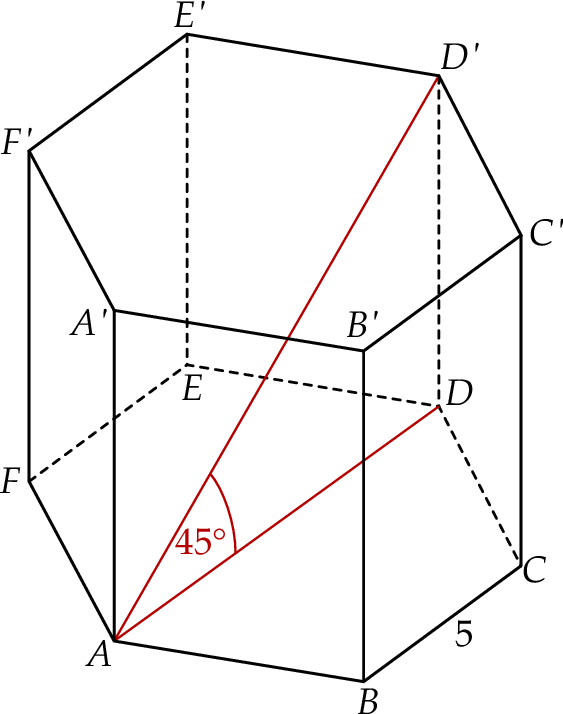
Pole ściany bocznej tego graniastosłupa jest równe
A) 12,5 B) 25 C) 50 D) 100
Dany jest graniastosłup prawidłowy sześciokątny 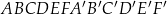 , w którym krawędź podstawy ma długość 3. Przekątna
, w którym krawędź podstawy ma długość 3. Przekątna 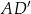 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 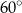 (zobacz rysunek).
(zobacz rysunek).
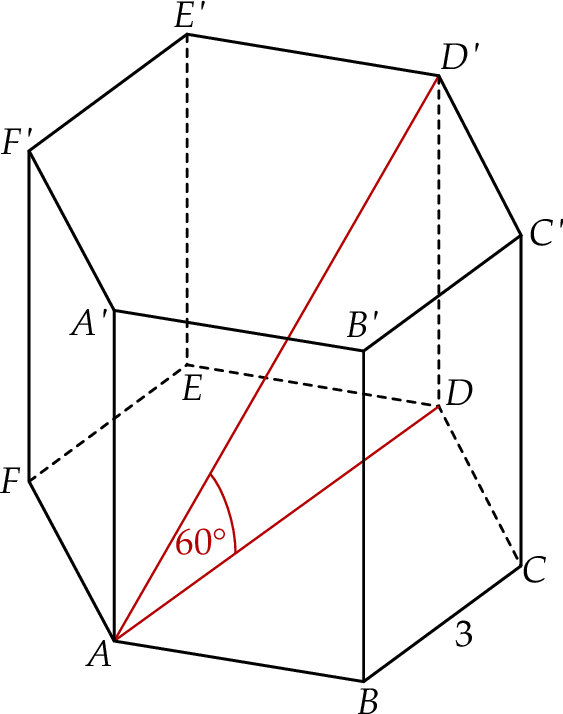
Pole ściany bocznej tego graniastosłupa jest równe
A) 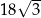 B)
B) 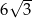 C)
C) 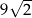 D) 90
D) 90
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa jest równy
A) 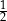 B)
B) 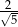 C)
C) 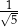 D)
D) 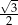
Wysokość graniastosłupa prawidłowego sześciokątnego jest równa 6 (zobacz rysunek).
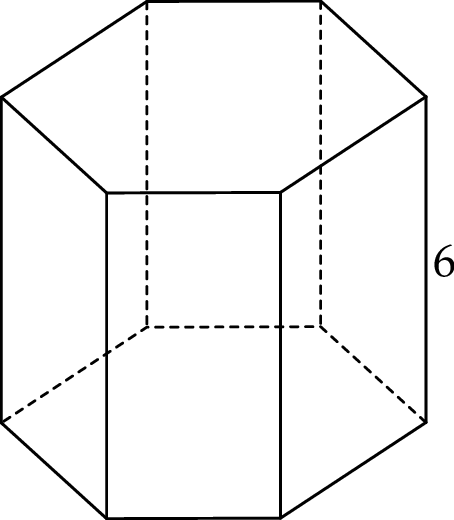
Pole podstawy tego graniastosłupa jest równe 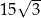 . Pole jednej ściany bocznej tego graniastosłupa jest równe
. Pole jednej ściany bocznej tego graniastosłupa jest równe
A) 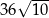 B) 60 C)
B) 60 C) 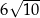 D) 360
D) 360
Dany jest graniastosłup prawidłowy sześciokątny 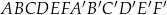 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 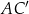 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 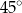 (zobacz rysunek).
(zobacz rysunek).

Objętość tego graniastosłupa jest równa
A) 225 B) 562,5 C) 112,5 D) 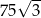
Każdą krawędź graniastosłupa prostego o podstawie będącej sześciokątem skrócono dwukrotnie. W wyniku tej zmiany pole powierzchni graniastosłupa zmniejszyło się o
A) 25% B) 50% C) 75% D) 100%
Każdą krawędź graniastosłupa prostego o podstawie będącej sześciokątem wydłużono dwukrotnie. W wyniku tej zmiany pole powierzchni graniastosłupa zwiększyło się o
A) 100% B) 300% C) 200% D) 400%
Liczba przekątnych graniastosłupa prawidłowego sześciokątnego jest równa
A) 12 B) 18 C) 6 D) 9
W graniastosłupie prawidłowym sześciokątnym 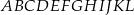 wierzchołki
wierzchołki 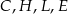 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
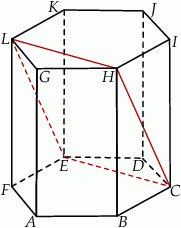
Wskaż kąt między bokiem 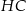 czworokąta
czworokąta 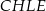 i płaszczyzną podstawy tego graniastosłupa.
i płaszczyzną podstawy tego graniastosłupa.
A) 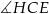 B)
B) 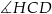 C)
C) 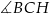 D)
D)