Uzasadnij, że jeśli 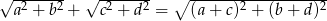 to
to 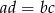 .
.
/Szkoła średnia/Liczby/Wyrażenia algebraiczne
Wykaż, że jeśli 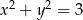 i
i 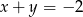 , to
, to 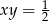 .
.
Wykaż, że jeśli 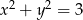 i
i 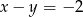 , to
, to 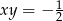 .
.
Udowodnij, że jeżeli liczba 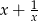 jest liczbą całkowitą, to liczba
jest liczbą całkowitą, to liczba 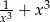 jest też liczbą całkowitą.
jest też liczbą całkowitą.
Oblicz  z równania
z równania 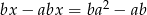 i przedstaw wynik w najprostszej postaci.
i przedstaw wynik w najprostszej postaci.
Oblicz  z równania
z równania 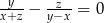 i przedstaw wynik w najprostszej postaci.
i przedstaw wynik w najprostszej postaci.
Oblicz  z równania
z równania 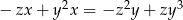 i przedstaw wynik w najprostszej postaci.
i przedstaw wynik w najprostszej postaci.
Udowodnij, że jeżeli liczby 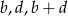 są różne od zera oraz
są różne od zera oraz 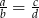 to
to 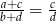 .
.
Udowodnij, że jeżeli liczby 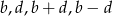 są różne od zera oraz
są różne od zera oraz 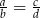 , to
, to 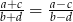 .
.
Udowodnij, że jeżeli liczby 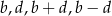 są różne od zera oraz
są różne od zera oraz 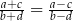 , to
, to 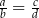 .
.
Wiadomo, że 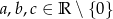 oraz
oraz 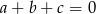 . Oblicz wartość sumy
. Oblicz wartość sumy
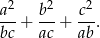
Suma dwóch liczb jest równa 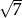 , a ich różnica jest równa
, a ich różnica jest równa 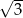 . Wykaż, że iloczyn tych liczb jest liczbą całkowitą.
. Wykaż, że iloczyn tych liczb jest liczbą całkowitą.
Oblicz wartość wyrażenia 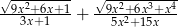 dla
dla 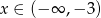 .
.
Uzasadnij, że jeżeli 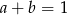 i
i 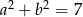 , to
, to 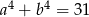 .
.
Uzasadnij, że jeżeli 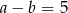 i
i 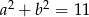 , to
, to 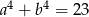 .
.
Wykaż, że jeżeli liczby rzeczywiste 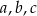 spełniają warunek
spełniają warunek  , to
, to
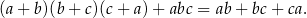
Między liczbami rzeczywistymi  i
i 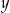 zachodzi związek
zachodzi związek 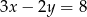 . Wyznacz najmniejszą wartość wyrażenia
. Wyznacz najmniejszą wartość wyrażenia 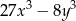 .
.
Wykaż, że jeżeli liczby  i
i 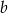 spełniają równość
spełniają równość 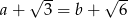 to przynajmniej jedna z nich jest niewymierna.
to przynajmniej jedna z nich jest niewymierna.
Wyznacz  ze wzoru
ze wzoru 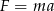 .
.
Wyznacz 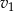 ze wzoru
ze wzoru 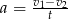 .
.
Wyznacz 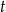 ze wzoru
ze wzoru 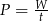 .
.
Wyznacz 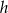 ze wzoru
ze wzoru 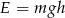 .
.
Wyznacz 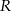 ze wzoru
ze wzoru 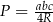 .
.
Wyznacz  ze wzoru
ze wzoru 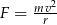 .
.
Wyznacz 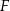 ze wzoru
ze wzoru 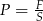 .
.
Wyznacz 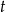 ze wzoru
ze wzoru 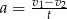 .
.
Wyznacz 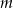 ze wzoru
ze wzoru 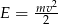 .
.
Liczby dodatnie  i
i 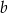 spełniają równość
spełniają równość 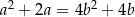 . Wykaż, że
. Wykaż, że 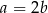 .
.
Liczby dodatnie  i
i 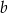 spełniają równość
spełniają równość 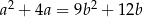 . Wykaż, że
. Wykaż, że 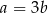 .
.
Wykaż, że dla dowolnych liczb dodatnich  i
i 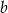 spełniona jest równość
spełniona jest równość
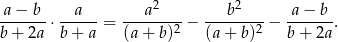
Wykaż, że jeżeli 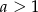 i
i 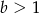 oraz
oraz 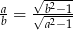 to
to 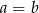 .
.
Uzasadni, że jeżeli liczby rzeczywiste 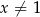 ,
, 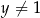 i
i 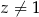 spełniają warunki:
spełniają warunki: 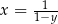 i
i 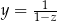 , to
, to 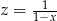 .
.
Skróć wyrażenie 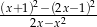 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Skróć wyrażenie 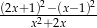 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Uzasadnij, że jeśli 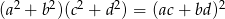 , to
, to 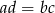 .
.
Rozważmy takie liczby rzeczywiste  i
i 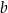 , które spełniają warunki:
, które spełniają warunki:
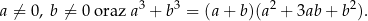
Oblicz wartość liczbową wyrażenia 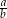 dla dowolnych liczb rzeczywistych
dla dowolnych liczb rzeczywistych  i
i 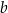 , spełniających powyższe warunki.
, spełniających powyższe warunki.

