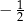Wielomian 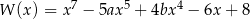 jest podzielny przez wielomian
jest podzielny przez wielomian 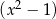 . Zatem
. Zatem
A) 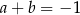 . B)
. B) 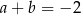 . C)
. C) 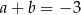 . D)
. D) 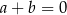 .
.
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Jeden wielomian/Z parametrem
Funkcja 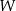 jest określona wzorem
jest określona wzorem 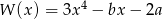 dla wszystkich liczb rzeczywistych. Równość
dla wszystkich liczb rzeczywistych. Równość 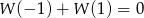 zachodzi, gdy
zachodzi, gdy
A) 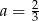 B)
B) 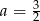 C)
C) 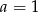 D)
D) 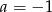
Dany jest wielomian 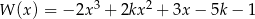 gdzie
gdzie 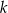 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 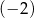 nie jest pierwiastkiem tego wielomianu. Zatem
nie jest pierwiastkiem tego wielomianu. Zatem
A) 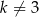 B)
B) 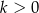 C)
C) 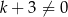 D)
D) 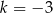
Wartość wielomianu 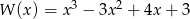 w punkcie
w punkcie 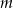 jest równa 15 dla
jest równa 15 dla
A) 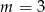 B)
B) 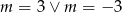 C)
C) 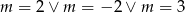 D)
D) 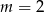
Wartość wielomianu 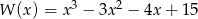 w punkcie
w punkcie 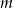 jest równa 3 dla
jest równa 3 dla
A) 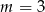 B)
B) 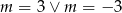 C)
C) 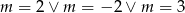 D)
D) 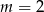
Wartość wielomianu 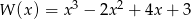 w punkcie
w punkcie  jest równa 11 dla
jest równa 11 dla
A) 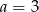 B)
B) 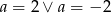 C)
C) 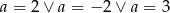 D)
D) 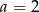
Funkcja 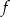 określona jest wzorem
określona jest wzorem 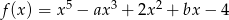 . Jeżeli
. Jeżeli 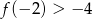 , to
, to
A) 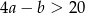 B)
B) 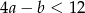 C)
C) 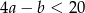 D)
D) 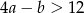
Wiadomo, że 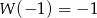 , gdy
, gdy 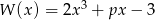 . Zatem wartość współczynnika
. Zatem wartość współczynnika 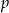 wynosi:
wynosi:
A) 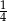 B) -4 C) 4 D) -1
B) -4 C) 4 D) -1
Dany jest wielomian 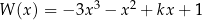 , gdzie
, gdzie 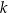 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 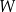 można zapisać w postaci
można zapisać w postaci 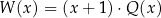 dla pewnego wielomianu
dla pewnego wielomianu 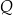 . Liczba
. Liczba 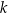 jest równa
jest równa
A) 29 B) 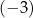 C) 0 D) 3
C) 0 D) 3
Dany jest wielomian 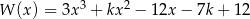 gdzie
gdzie 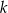 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 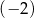 jest pierwiastkiem tego wielomianu. Liczba
jest pierwiastkiem tego wielomianu. Liczba 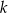 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Dany jest wielomian 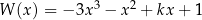 , gdzie
, gdzie 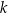 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 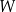 można zapisać w postaci
można zapisać w postaci 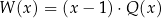 dla pewnego wielomianu
dla pewnego wielomianu 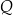 . Liczba
. Liczba 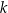 jest równa
jest równa
A) 29 B) 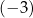 C) 0 D) 3
C) 0 D) 3
Dany jest wielomian 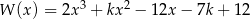 gdzie
gdzie 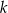 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 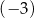 jest pierwiastkiem tego wielomianu. Liczba
jest pierwiastkiem tego wielomianu. Liczba 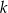 jest równa
jest równa
A) 2 B) 3 C) 6 D) 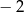
Wiadomo, że 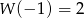 , gdy
, gdy 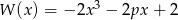 . Zatem wartość współczynnika
. Zatem wartość współczynnika 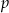 wynosi:
wynosi:
A) 6 B) -3 C) 3 D) -1
Dany jest wielomian 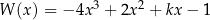 , gdzie
, gdzie 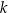 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 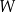 można zapisać w postaci
można zapisać w postaci 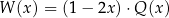 dla pewnego wielomianu
dla pewnego wielomianu 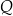 . Liczba
. Liczba 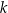 jest równa
jest równa
A) 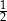 B) 2 C)
B) 2 C) 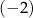 D)
D)