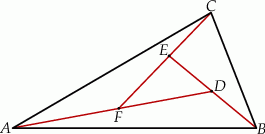
W trójkącie 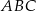 poprowadzono odcinki
poprowadzono odcinki 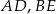 i
i 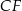 w ten sposób, że punkty
w ten sposób, że punkty 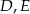 i
i 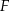 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 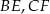 i
i 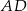 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 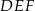 jest siedem razy mniejsze od pola trójkąta
jest siedem razy mniejsze od pola trójkąta  .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie  poprowadzono odcinki
poprowadzono odcinki 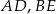 i
i 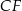 w ten sposób, że punkty
w ten sposób, że punkty 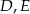 i
i 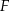 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 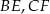 i
i 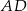 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 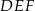 jest siedem razy mniejsze od pola trójkąta
jest siedem razy mniejsze od pola trójkąta 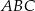 .
.

Na bokach trójkąta 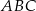 zbudowano kwadraty
zbudowano kwadraty 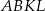 ,
, 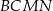 i
i 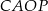 (zobacz rysunek).
(zobacz rysunek).
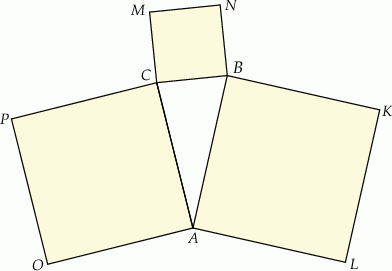
Kąty 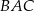 i
i 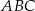 są ostre oraz suma ich tangensów jest równa
są ostre oraz suma ich tangensów jest równa  . Wykaż, że jeżeli pole kwadratu
. Wykaż, że jeżeli pole kwadratu 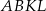 jest pięć razy większe od pola trójkąta
jest pięć razy większe od pola trójkąta 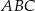 , to suma pól kwadratów
, to suma pól kwadratów 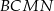 i
i 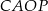 też jest pięć razy większa od pola trójkąta
też jest pięć razy większa od pola trójkąta 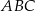 .
.
W trójkącie 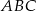 bok
bok 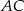 ma długość
ma długość 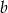 ,
, 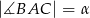 oraz
oraz 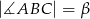 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 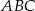 jest równe
jest równe
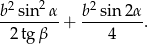
Wykaż, że pole trójkąta o bokach 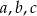 i promieniu
i promieniu 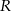 okręgu opisanego na nim jest równe
okręgu opisanego na nim jest równe 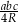 .
.
Wykaż, że pole trójkąta 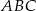 jest równe
jest równe 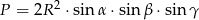 , gdzie
, gdzie 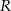 jest promieniem okręgu opisanego na tym trójkącie, a
jest promieniem okręgu opisanego na tym trójkącie, a 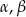 i
i 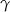 są miarami kątów wewnętrznych tego trójkąta.
są miarami kątów wewnętrznych tego trójkąta.
Na bokach 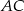 i
i 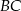 trójkąta
trójkąta 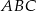 obrano punkty
obrano punkty 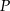 i
i 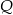 takie, że
takie, że 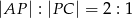 oraz
oraz 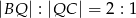 . Odcinki
. Odcinki 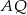 i
i 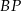 przecinają się w punkcie
przecinają się w punkcie 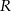 . Wykaż, że pole czworokąta
. Wykaż, że pole czworokąta 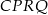 jest równe polu trójkąta
jest równe polu trójkąta 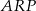 .
.
Uzasadnij wzór na pole trójkąta 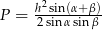 , gdzie
, gdzie  i
i 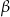 są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość
są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość 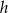 .
.
Punkty 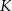 i
i 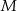 oraz
oraz 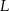 i
i 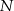 dzielą odpowiednio boki
dzielą odpowiednio boki 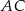 i
i 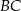 trójkąta
trójkąta 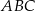 w stosunku
w stosunku 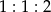 (zobacz rysunek). Odcinki
(zobacz rysunek). Odcinki 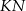 i
i 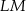 przecinają się w punkcie
przecinają się w punkcie 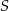 .
.
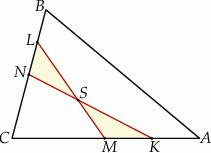
Uzasadnij, że pola trójkątów 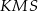 i
i 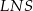 są równe.
są równe.
Punkty 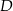 i
i 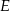 dzielą bok
dzielą bok 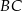 trójkąta
trójkąta 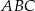 na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta
na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta 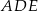 jest trzy razy mniejsze od pola trójkąta
jest trzy razy mniejsze od pola trójkąta  .
.
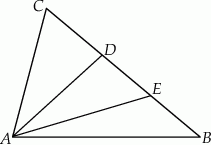
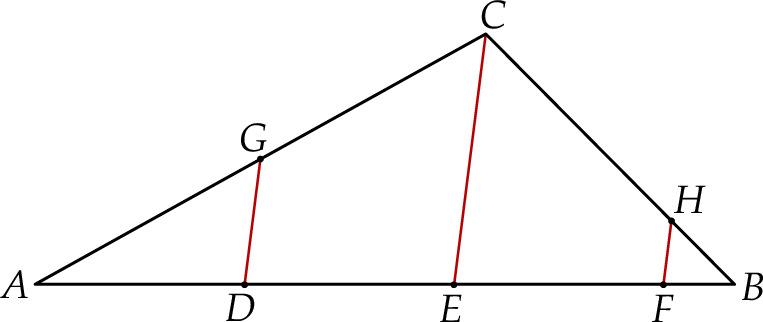
Dany jest trójkąt  . Na boku
. Na boku  tego trójkąta obrano punkty
tego trójkąta obrano punkty 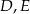 i
i 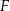 tak, że
tak, że 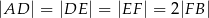 . Na bokach
. Na bokach 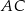 i
i 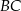 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 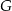 i
i 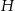 tak, że
tak, że 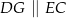 oraz
oraz 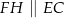 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 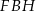 jest równe
jest równe 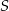 , to pole trójkąta
, to pole trójkąta 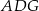 jest równe
jest równe 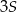 .
.
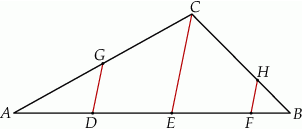
Dany jest trójkąt 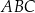 . Na boku
. Na boku 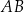 tego trójkąta obrano punkty
tego trójkąta obrano punkty 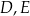 i
i 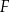 tak, że
tak, że 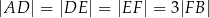 . Na bokach
. Na bokach 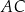 i
i 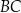 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 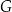 i
i 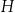 tak, że
tak, że 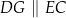 oraz
oraz 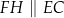 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 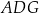 jest równe
jest równe 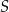 , to pole trójkąta
, to pole trójkąta 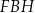 jest równe
jest równe 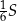 .
.
Punkty 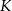 i
i 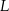 są środkami boków
są środkami boków 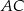 i
i 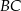 trójkąta
trójkąta 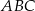 . Odcinki
. Odcinki 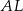 i
i 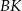 przecinają się w punkcie
przecinają się w punkcie 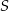 .
.
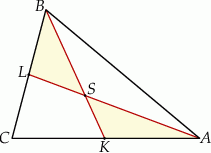
Uzasadnij, że pola trójkątów 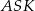 i
i 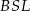 są równe.
są równe.
