W okręgu o promieniu 5 poprowadzono dwie równoległe cięciwy o długościach 6 i 8. Oblicz odległość między tymi cięciwami.
/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Oblicz długość
Z punktu leżącego na okręgu o promieniu 5 poprowadzono dwie prostopadłe cięciwy. Różnica ich długości jest równa 2. Oblicz długości tych cięciw.
Z punktu leżącego na okręgu o promieniu 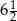 poprowadzono dwie prostopadłe cięciwy. Różnica ich długości jest równa 7. Oblicz długości tych cięciw.
poprowadzono dwie prostopadłe cięciwy. Różnica ich długości jest równa 7. Oblicz długości tych cięciw.
Dany jest okrąg 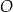 o środku w punkcie
o środku w punkcie 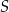 . Średnica
. Średnica 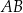 tego okręgu przecina cięciwę
tego okręgu przecina cięciwę 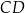 w punkcie
w punkcie 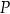 (zobacz rysunek). Ponadto:
(zobacz rysunek). Ponadto: 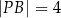 ,
, 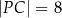 oraz
oraz 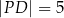 .
.
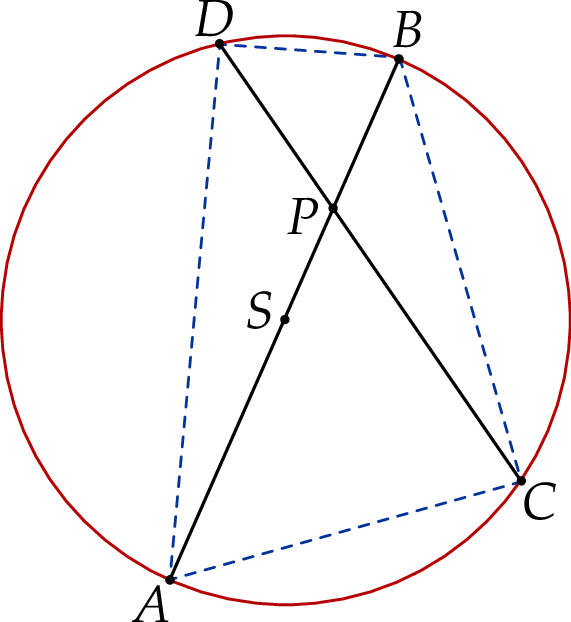
Oblicz promień okręgu 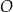 .
.
Dany jest okrąg 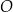 o środku w punkcie
o środku w punkcie 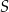 . Średnica
. Średnica 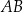 tego okręgu przecina cięciwę
tego okręgu przecina cięciwę 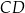 w punkcie
w punkcie 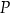 (zobacz rysunek). Ponadto:
(zobacz rysunek). Ponadto: 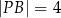 ,
, 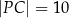 oraz
oraz 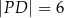 .
.
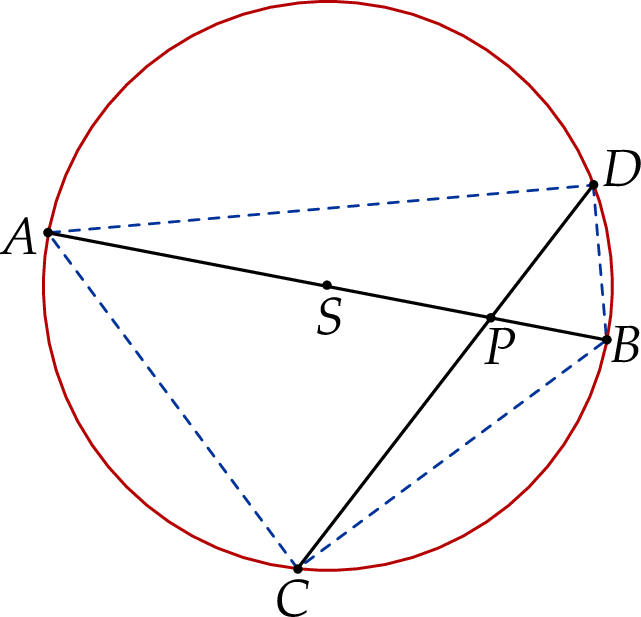
Oblicz promień okręgu 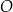 .
.
Dwa okręgi o środkach 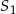 i
i 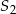 przecinają się w punktach
przecinają się w punktach 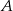 i
i 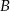 , przy czym punkty
, przy czym punkty 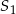 i
i 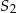 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 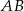 .
.
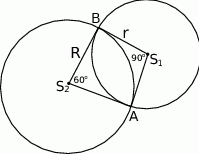
Miary kątów 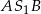 i
i 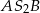 wynoszą odpowiednio
wynoszą odpowiednio 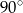 i
i 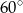 . Wyznacz stosunek
. Wyznacz stosunek 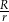 długości promieni tych okręgów.
długości promieni tych okręgów.
W kole o środku 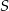 poprowadzono cięciwę, która nie jest średnicą. Punkt
poprowadzono cięciwę, która nie jest średnicą. Punkt 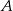 dzieli tę cięciwę na dwa odcinki o długościach 11 i 29. Odcinek
dzieli tę cięciwę na dwa odcinki o długościach 11 i 29. Odcinek 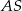 ma długość 15. Oblicz promień tego koła.
ma długość 15. Oblicz promień tego koła.
Przez środek 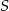 cięciwy
cięciwy 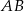 okręgu poprowadzono cięciwę
okręgu poprowadzono cięciwę 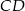 , przy czym
, przy czym 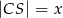 i
i 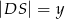 . Oblicz długość cięciwy
. Oblicz długość cięciwy 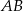 .
.
Dany jest okrąg 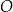 o środku w punkcie
o środku w punkcie 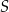 . Przedłużenie średnicy
. Przedłużenie średnicy 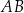 tego okręgu przecina przedłużenie cięciwy
tego okręgu przecina przedłużenie cięciwy 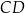 w punkcie
w punkcie 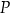 (zobacz rysunek). Ponadto:
(zobacz rysunek). Ponadto: 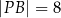 ,
, 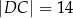 oraz
oraz 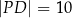 .
.
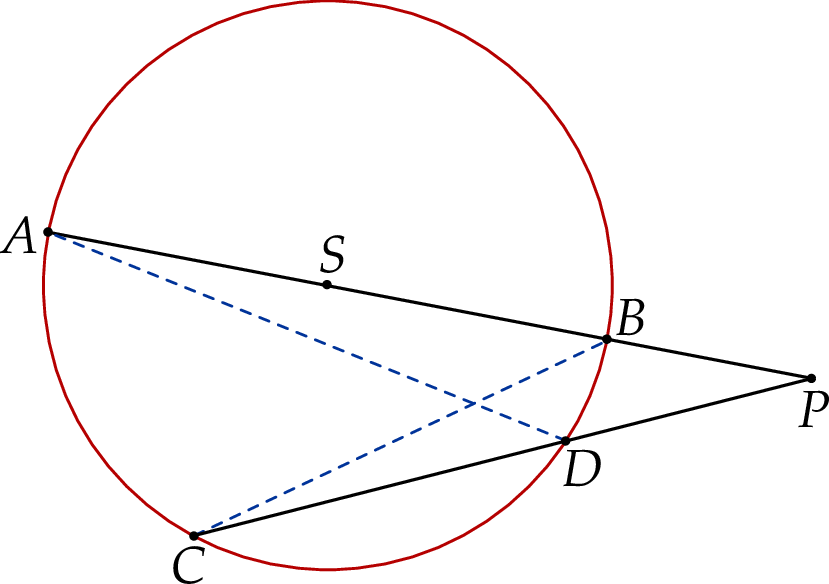
Oblicz promień okręgu 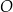 .
.
W kole poprowadzono cięciwę i średnicę. Cięciwa dzieli średnicę na odcinki o długościach 2 oraz 10 i tworzy z nią kąt o mierze 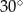 . Oblicz odległość środka okręgu od cięciwy.
. Oblicz odległość środka okręgu od cięciwy.
Promienie okręgów 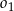 i
i 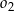 są równe odpowiednio
są równe odpowiednio 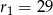 i
i 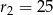 , a odległość między środkami tych okręgów jest równa 36. Oblicz długość odcinka łączącego punkty wspólne okręgów
, a odległość między środkami tych okręgów jest równa 36. Oblicz długość odcinka łączącego punkty wspólne okręgów 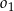 i
i 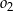 .
.
Środek okręgu leży w odległości 10 cm od cięciwy tego okręgu. Długość tej cięciwy jest o 22 cm większa od promienia tego okręgu. Oblicz promień tego okręgu.
Środek okręgu leży w odległości 8 cm od cięciwy tego okręgu. Długość tej cięciwy jest o 13 cm większa od promienia tego okręgu. Oblicz promień tego okręgu.
W okręgu o promieniu 6 średnice 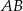 i
i 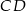 przecinają się pod kątem
przecinają się pod kątem 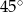 . Na okręgu tym wybrano punkt
. Na okręgu tym wybrano punkt 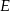 oraz skonstruowano jego rzuty
oraz skonstruowano jego rzuty 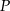 i
i 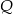 odpowiednio na średnice
odpowiednio na średnice 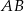 i
i 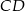 . Oblicz długość odcinka
. Oblicz długość odcinka 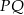 .
.
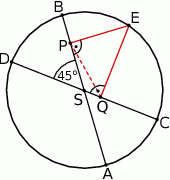
W okręgu o promieniu długości  kreślimy średnicę
kreślimy średnicę 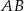 oraz taką cięciwę
oraz taką cięciwę 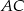 , że
, że 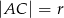 . Jaką częścią okręgu jest łuk
. Jaką częścią okręgu jest łuk 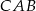 ?
?
Dwie cięciwy przecinają się wewnątrz okręgu tak, że odcinki jednej z nich mają długości 8 i 6, a odcinki drugiej pozostają w stosunku 2:3. Podaj długości odcinków drugiej cięciwy.
Dane jest koło o promieniu długości 16 cm. W kole tym poprowadzono cięciwę opartą na łuku odpowiadającym kątowi środkowemu o mierze 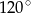 . Znajdź odległość tej cięciwy od środka koła.
. Znajdź odległość tej cięciwy od środka koła.
Dwa okręgi o środkach 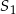 i
i 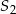 przecinają się w punktach
przecinają się w punktach 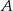 i
i 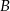 , przy czym punkty
, przy czym punkty 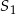 i
i 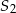 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 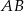 . Miary kątów
. Miary kątów 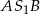 i
i 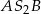 wynoszą odpowiednio
wynoszą odpowiednio 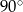 i
i 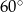 . Wyznacz długości promieni tych okręgów wiedząc, że
. Wyznacz długości promieni tych okręgów wiedząc, że 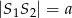 .
.
Dany jest okrąg o promieniu 11 oraz punkt 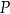 oddalony o 7 od środka okręgu. Przez punkt
oddalony o 7 od środka okręgu. Przez punkt 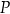 poprowadzono cięciwę o długości 18. W jakim stosunku punkt
poprowadzono cięciwę o długości 18. W jakim stosunku punkt 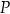 podzielił tę cięciwę na dwa odcinki?
podzielił tę cięciwę na dwa odcinki?

