Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 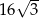 , a jego objętość
, a jego objętość 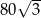 . Wyznacz cosinus kąta
. Wyznacz cosinus kąta  nachylenia ściany bocznej do płaszczyzny podstawy.
nachylenia ściany bocznej do płaszczyzny podstawy.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 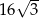 , a jego objętość
, a jego objętość 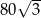 . Wyznacz cosinus kąta
. Wyznacz cosinus kąta  nachylenia ściany bocznej do płaszczyzny podstawy.
nachylenia ściany bocznej do płaszczyzny podstawy.

Objętość ostrosłupa prawidłowego trójkątnego 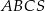 (tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę 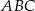 tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
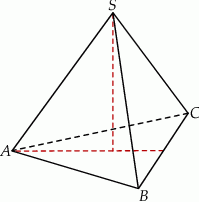
Objętość ostrosłupa prawidłowego trójkątnego 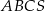 (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie
(patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 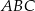 tego ostrosłupa jest równy 2. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
tego ostrosłupa jest równy 2. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
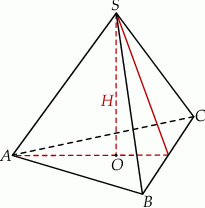
Objętość ostrosłupa prawidłowego trójkątnego 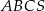 (tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę 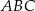 tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.
tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.
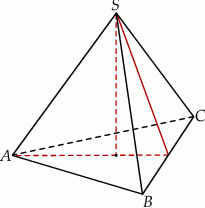
Objętość ostrosłupa prawidłowego trójkątnego 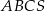 (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie
(patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 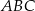 tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
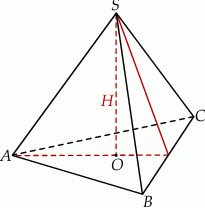
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 6, a krawędź podstawy ma długość 3. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
W ostrosłupie prawidłowym trójkątnym stosunek pola powierzchni bocznej do pola podstawy jest równe 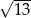 . Oblicz miarę kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy.
. Oblicz miarę kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy.
W ostrosłupie prawidłowym trójkątnym 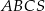 krawędź podstawy ma długość
krawędź podstawy ma długość  . Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy.
. Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy.
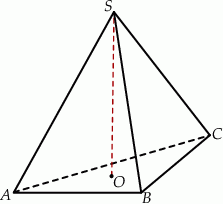
W ostrosłupie prawidłowym trójkątnym  pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
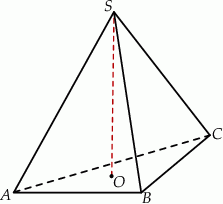
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 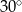 . Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest 2 razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta utworzonego przez dwie sąsiednie ściany boczne.
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta utworzonego przez dwie sąsiednie ściany boczne.
Oblicz cosinus kąta między ścianą boczną i płaszczyzną podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.
Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.
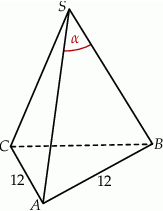
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 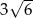 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
, a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
W ostrosłupie prawidłowym trójkątnym 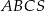 krawędź podstawy ma długość 12, a jego objętość jest równa
krawędź podstawy ma długość 12, a jego objętość jest równa 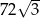 . Kąt
. Kąt  jest kątem między krawędziami bocznymi
jest kątem między krawędziami bocznymi 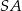 i
i 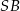 (zobacz rysunek). Oblicz sinus kąta
(zobacz rysunek). Oblicz sinus kąta  .
.
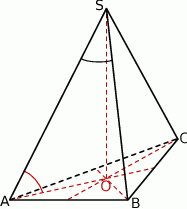
Podstawą ostrosłupa prawidłowego trójkątnego 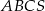 jest trójkąt
jest trójkąt 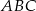 . Kąt nachylenia krawędzi bocznej
. Kąt nachylenia krawędzi bocznej 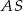 do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi
do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi 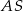 i
i 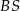 zawartymi w ścianie bocznej
zawartymi w ścianie bocznej 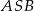 tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego równa się 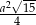 , gdzie
, gdzie  oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem
oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem 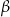 . Oblicz
. Oblicz 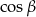 i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość
i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość 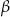 z dokładnością do
z dokładnością do 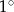 .
.
Dane są dwie bryły: stożek, w którym długość promienia podstawy jest równa 2 dm i wysokość ma długość 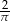 dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
