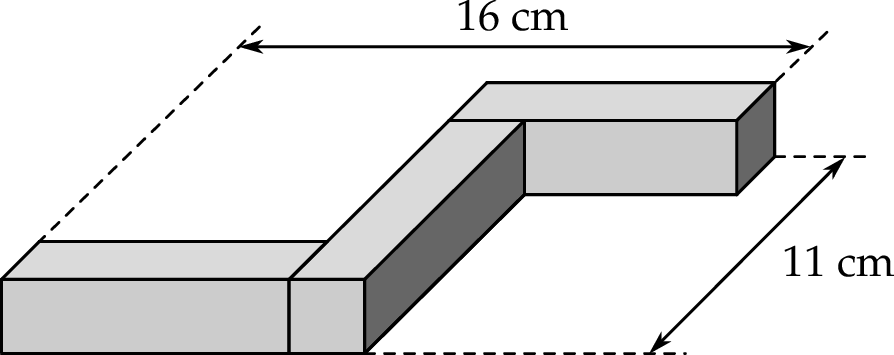
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 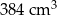 .
.
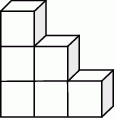
Pole powierzchni całkowitej tej bryły jest równe
A) 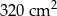 B)
B) 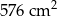 C)
C) 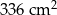 D)
D) 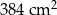
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 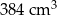 .
.

Pole powierzchni całkowitej tej bryły jest równe
A) 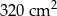 B)
B) 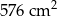 C)
C) 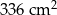 D)
D) 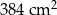
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 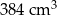 .
.
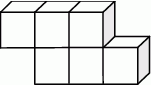
Pole powierzchni całkowitej tej bryły jest równe
A) 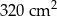 B)
B) 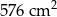 C)
C) 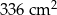 D)
D) 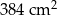
Na siatce sześcianu zaznaczono jego dwie ściany 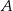 i
i 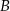 oraz jego dwie krawędzie
oraz jego dwie krawędzie 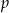 i
i 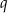 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ściany  i i  są przeciwległymi ścianami sześcianu. są przeciwległymi ścianami sześcianu. | P | F |
Krawędzie 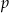 i i 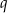 są prostopadłymi krawędziami sześcianu. są prostopadłymi krawędziami sześcianu. | P | F |
Oskar wykonał model prostopadłościanu. Układał i sklejał ze sobą kolejno drewniane klocki sześcienne o krawędzi 4 cm wzdłuż każdej ściany prostopadłościennego pudełka o wymiarach: 36 cm, 28 cm, 20 cm. Na rysunku przedstawiono część wykonanego modelu (model jest w środku pusty).
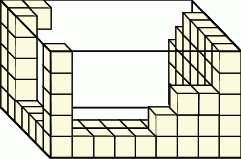
Ile klocków łącznie zużył Oskar na wykonanie całego modelu?
A) 315 B) 230 C) 246 D) 210
Bryłę ułożono z jednakowych sześciennych klocków. Na rysunkach przedstawiony jest widok tej bryły z dwóch stron.
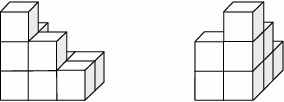
Z ilu klocków składa się ta bryła?
A) 7 B) 8 C) 9 D) 10
Każdy z dwóch jednakowych sześcianów o krawędzi 2 cm podzielono na mniejsze sześciany o krawędzi 1 cm. Czy z otrzymanych w ten sposób małych sześciennych kostek można ułożyć jeden pełny sześcian, tak by wszystkie kostki były wykorzystane? Wybierz odpowiedź T lub N i jej uzasadnienie wybrane spośród A, B, C, D.
| Tak | Nie |
| ponieważ | |
| A) | Liczba małych kostek nie jest podzielna przez 3. |
| B) | Liczba małych kostek jest potęgą liczby 2. |
| C) | Liczba małych kostek jest drugą potęgą liczby naturalnej. |
| D) | Liczba małych kostek nie jest trzecią potęgą liczby naturalnej. |
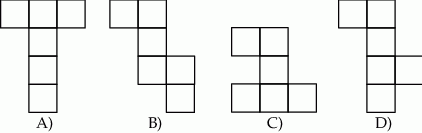
Który z poniższych rysunków nie może być siatką sześcianu?
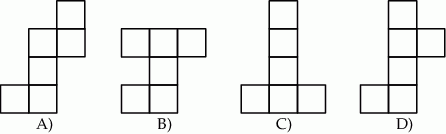
Który z poniższych rysunków nie może być siatką sześcianu?
Witek ma trzy jednakowe prostopadłościenne klocki. W każdym z tych klocków dwie ściany są kwadratami, a cztery pozostałe – prostokątami. Z tych klocków zbudował figurę przedstawioną na rysunku.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dłuższe krawędzie prostopadłościennego klocka mają po 8 cm. | P | F |
Objętość jednego klocka jest równa  . . | P | F |
W koszu były 203 jednakowe sześcienne klocki. Zbudowano z nich możliwie największy sześcian, a pozostałe odłożono. Ile klocków odłożono?
A) 150 B) 125 C) 78 D) 53
W koszu były 303 jednakowe sześcienne klocki. Zbudowano z nich możliwie największy sześcian, a pozostałe odłożono. Ile klocków odłożono?
A) 87 B) 125 C) 178 D) 216
Drewniany sześcian rozcięto na identyczne mniejsze sześciany, a następnie usunięto część z nich tworząc trzy puste tunele łączące przeciwległe ściany (zobacz rysunek). Otrzymana w ten sposób bryła została w całości zanurzona w niebieskiej farbie.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Otrzymana bryła składa się ze 110 małych sześcianów. | P | F |
| 24 małe sześciany mają dokładnie jedną ścianę pomalowaną na niebiesko. | P | F |
Dwa sześciany – jeden o krawędzi 2 i drugi o krawędzi 3 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 35 B) 47 C) 94 D) 142
Dwa sześciany – jeden o krawędzi 3 i drugi o krawędzi 4 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 150 B) 222 C) 366 D) 111
Jacek z 14 jednakowych sześciennych kostek skleił figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.
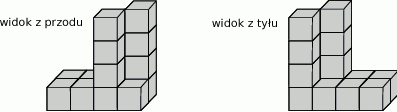
Całą figurę, również od spodu, Jacek pomalował. Ile sześciennych kostek ma pomalowane dokładnie 4 ściany?
A) 8 B) 7 C) 6 D) 5
Dagmara z 20 jednakowych sześciennych kostek skleiła figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.

Całą figurę, również od spodu, Dagmara pomalowała. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dokładnie 7 kostek ma pomalowane dokładnie 3 ściany. | P | F |
| Dokładnie 7 kostek ma pomalowane dokładnie 2 ściany. | P | F |
Z 36 sześcianów o krawędziach długości 1 zbudowano graniastosłup prawidłowy czworokątny. Które wymiary, z podanych w tabeli, może mieć ten graniastosłup?
| I | 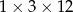 |
| II | 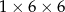 |
| III | 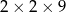 |
| IV | 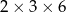 |
| V | 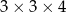 |
A) I, II i III B) III, IV i V C) I, II i IV D) II, III i V E) Wszystkie podane.
Z 9 sześcianów o krawędziach długości 2 zbudowano graniastosłup prawidłowy czworokątny. Które wymiary, z podanych w tabeli, może mieć ten graniastosłup?
| I | 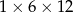 |
| II | 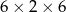 |
| III | 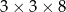 |
| IV | 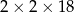 |
| V | 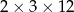 |
A) II, III i IV B) III i IV C) II i IV D) Wszystkie podane.
Na rysunku poniżej przedstawiono siatkę sześcianu. Punkty: 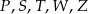 są środkami jego krawędzi.
są środkami jego krawędzi.
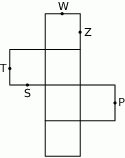
Po złożeniu sześcianu z tej siatki punkt 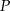 pokryje się z punktem
pokryje się z punktem
A) 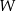 B)
B) 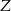 C)
C) 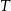 D)
D) 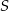
Na rysunku poniżej przedstawiono siatkę sześcianu. Punkty: 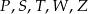 są środkami jego krawędzi.
są środkami jego krawędzi.
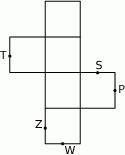
Po złożeniu sześcianu z tej siatki punkt 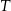 pokryje się z punktem
pokryje się z punktem
A) 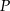 B)
B) 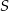 C)
C) 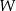 D)
D) 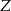
Jedną ścianę drewnianego sześcianu pomalowano na czerwono, a pozostałe – na biało. Ten sześcian rozcięto na 27 jednakowych sześcianów. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Tylko cztery małe sześciany mają dokładnie jedną ścianę pomalowaną na biało. | P | F |
| Tylko cztery małe sześciany mają trzy ściany pomalowane na biało. | P | F |
Dwie przeciwległe ściany drewnianego sześcianu pomalowano na czerwono, a pozostałe – na biało. Ten sześcian rozcięto na 27 jednakowych sześcianów. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Sześć małych sześcianów ma dokładnie jedną ścianę pomalowaną farbą. | P | F |
| Tylko cztery małe sześciany mają jedną ścianę pomalowaną na biało. | P | F |
Prostopadłościan o wymiarach 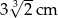 ,
, 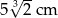 i
i 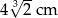 podzielono na 60 jednakowych sześcianów. Objętość jednego sześcianu jest równa
podzielono na 60 jednakowych sześcianów. Objętość jednego sześcianu jest równa
A) 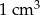 B)
B) 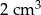 C)
C) 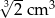 D)
D) 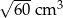
Z sześcianu o objętości 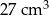 usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe
usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe
A) 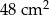 B)
B) 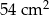 C)
C) 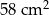 D)
D) 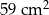
W koszu znajdowały się jednakowe sześcienne klocki, których ściany są kwadratami o polu powierzchni 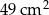 . Z wszystkich tych klocków zbudowano prostopadłościan o objętości
. Z wszystkich tych klocków zbudowano prostopadłościan o objętości 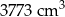 . W koszu znajdowało się A/B klocków.
. W koszu znajdowało się A/B klocków.
A) 11 B) 77
Pole powierzchni całkowitej zbudowanego prostopadłościanu jest równe C/D.
C) 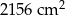 D)
D) 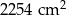
Sześcian o objętości 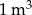 rozcięto na sześciany o krawędzi 1 cm. Gdyby wszystkie otrzymane sześciany ustawiono jeden za drugim, tak jak na rysunku, to powstałby prostopadłościan.
rozcięto na sześciany o krawędzi 1 cm. Gdyby wszystkie otrzymane sześciany ustawiono jeden za drugim, tak jak na rysunku, to powstałby prostopadłościan.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jedna z krawędzi powstałego prostopadłościanu miałaby długość 10 km. | P | F |
| Objętość prostopadłościanu byłaby 100 razy większa od objętości początkowego sześcianu. | P | F |
Z 1 000 000 sześcianów o objętości 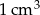 zbudowano prostopadłościan o polu podstawy równym
zbudowano prostopadłościan o polu podstawy równym 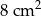 .
.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość prostopadłościanu jest równa 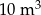 . . | P | F |
| Wysokość prostopadłościanu jest równa 1,25 km. | P | F |
Sześcian o krawędzi długości 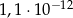 ma objętość równą
ma objętość równą
A) 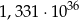 B)
B) 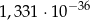 C)
C) 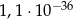 D)
D) 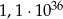
Z przedstawionych na rysunku siatek sklejono cztery sześciany.

W ilu z tych sześcianów naprzeciwko ściany oznaczonej literą 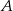 znajduje się ściana oznaczona literą
znajduje się ściana oznaczona literą 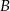 ?
?
A) 1 B) 2 C) 3 D) 4
