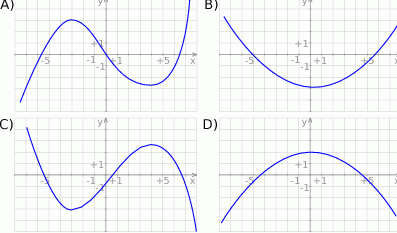
Rysunek przedstawia wykres funkcji 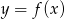 .
.
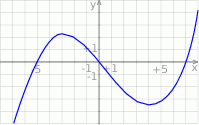
Wskaż wykres funkcji 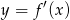 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rysunek przedstawia wykres funkcji 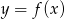 .
.

Wskaż wykres funkcji 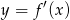 .
.

Rysunek przedstawia wykres funkcji 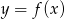 .
.
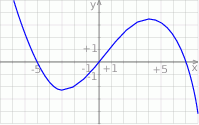
Wskaż wykres funkcji 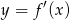 .
.
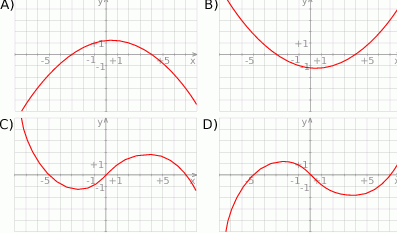
Na rysunku przedstawiono fragment wykresu pochodnej 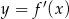 funkcji
funkcji 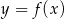 .
.
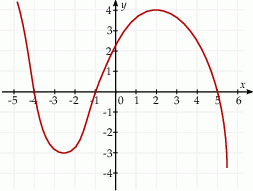
Funkcja 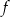 jest rosnąca w przedziale
jest rosnąca w przedziale
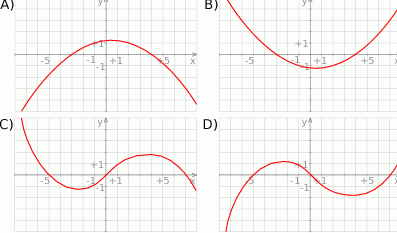
A) 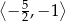 B)
B) 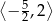 C)
C) 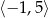 D)
D) 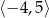
Na rysunku przedstawiono fragment wykresu pochodnej 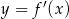 funkcji
funkcji 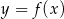 .
.
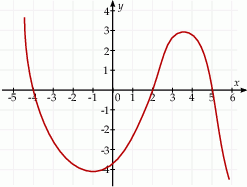
Funkcja 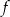 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 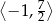 B)
B) 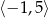 C)
C) 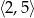 D)
D) 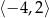
Na rysunku przedstawiono fragment wykresu pochodnej 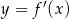 funkcji
funkcji 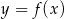 .
.
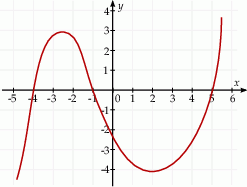
Funkcja 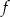 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 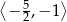 B)
B) 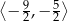 C)
C) 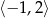 D)
D) 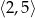
Na rysunku przedstawiono fragment wykresu pochodnej 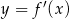 funkcji
funkcji 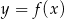 .
.
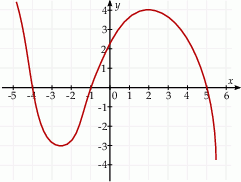
Funkcja 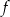 jest malejąca w przedziale
jest malejąca w przedziale
A) 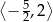 B)
B) 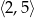 C)
C) 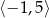 D)
D) 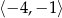
Na rysunku przedstawiono fragment wykresu pochodnej 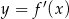 funkcji
funkcji 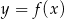 .
.
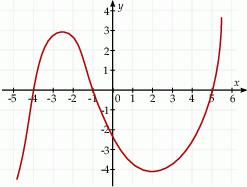
Funkcja 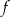 jest malejąca w przedziale
jest malejąca w przedziale
A) 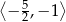 B)
B) 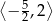 C)
C) 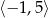 D)
D) 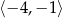
Na rysunku przedstawiono fragment wykresu pochodnej 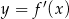 funkcji
funkcji 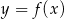 .
.
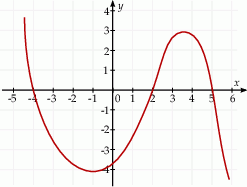
Funkcja 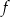 jest malejąca w przedziale
jest malejąca w przedziale
A) 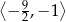 B)
B) 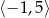 C)
C) 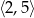 D)
D) 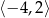
Na rysunku przedstawiono fragment wykresu pochodnej 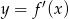 funkcji
funkcji 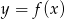 .
.
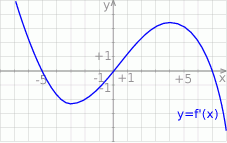
Wynika stąd, że funkcja 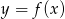 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 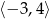 B)
B) 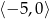 C)
C) 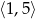 D)
D) 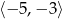
Na rysunku przedstawiono fragment wykresu pochodnej 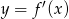 funkcji
funkcji 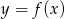 .
.
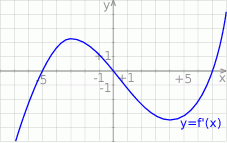
Wynika stąd, że funkcja 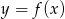 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 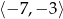 B)
B) 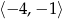 C)
C) 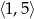 D)
D) 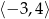
Wykres której z poniższych funkcji nie posiada asymptoty poziomej?
A) 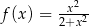 B)
B) 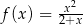 C)
C) 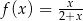 D)
D) 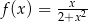
Proste 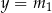 i
i 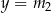 , gdzie
, gdzie 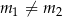 są styczne do wykresu funkcji
są styczne do wykresu funkcji 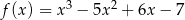 w punktach
w punktach 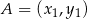 i
i 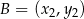 . Zatem
. Zatem
A) 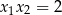 B)
B) 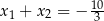 C)
C) 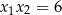 D)
D) 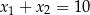
Na rysunku przedstawiono fragment wykresu pochodnej 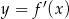 funkcji
funkcji 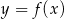 .
.
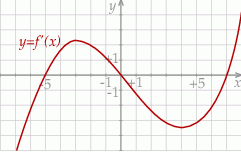
Wynika stąd, że
A) 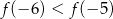 B)
B) 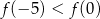 C)
C) 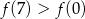 D)
D) 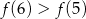
Na rysunku przedstawiono fragment wykresu pochodnej 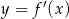 funkcji
funkcji 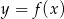 .
.
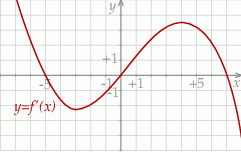
Wynika stąd, że
A) 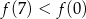 B)
B) 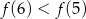 C)
C) 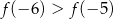 D)
D) 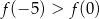
Na rysunku przedstawiono fragment wykresu funkcji 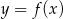
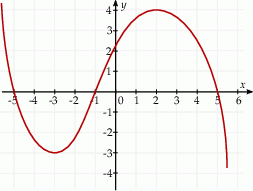
Pochodna 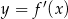 funkcji
funkcji 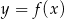 jest dodatnia w przedziale
jest dodatnia w przedziale
A) 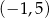 B)
B) 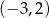 C)
C) 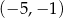 D)
D) 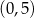
Na rysunku przedstawiono fragment wykresu pochodnej 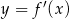 funkcji
funkcji 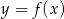 .
.
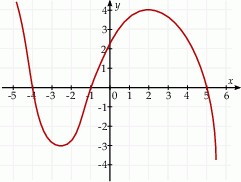
Funkcja 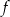 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A) 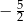 B)
B) 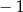 C)
C) 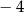 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 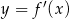 funkcji
funkcji 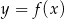 .
.
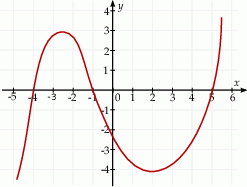
Funkcja 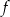 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A) 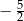 B)
B) 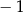 C)
C) 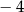 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 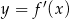 funkcji
funkcji 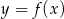 .
.
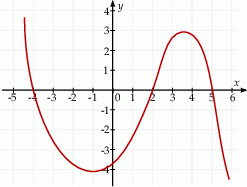
Funkcja 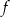 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A)  B)
B) 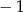 C)
C) 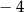 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 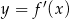 funkcji
funkcji 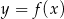 .
.
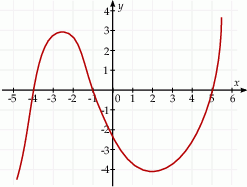
Funkcja 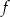 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A) 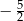 B)
B) 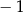 C)
C) 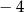 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 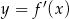 funkcji
funkcji 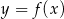 .
.
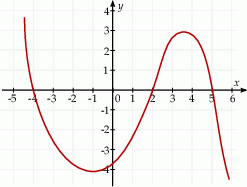
Funkcja 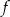 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A)  B)
B) 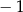 C)
C) 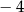 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 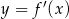 funkcji
funkcji 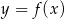 .
.
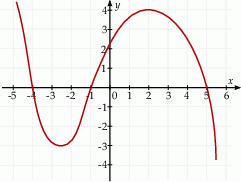
Funkcja 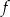 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A) 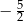 B)
B) 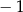 C)
C) 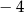 D) 2
D) 2
Rysunek przedstawia wykres funkcji 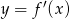 .
.
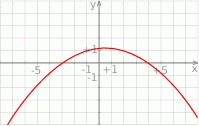
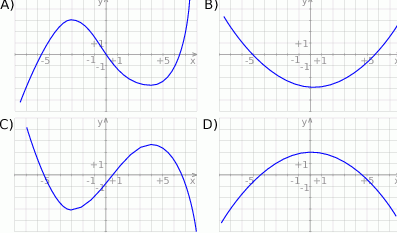
Wskaż wykres funkcji 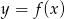 .
.
Rysunek przedstawia wykres funkcji 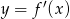 .
.
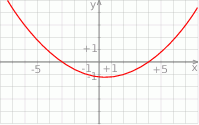
Wskaż wykres funkcji 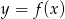 .
.