Kostki/Z definicji/Prawdopodobieństwo - zadania z matematyki

/Szkoła średnia/Prawdopodobieństwo/Z definicji/Kostki

Rzucamy dwiema sześciennymi kostkami.

Jakie jest prawdopodobieństwo, że suma oczek będzie równa 4?
Czy bardziej prawdopodobne jest, że suma wyrzuconych oczek będzie równa 5, czy że będzie równa 10?
Jakie jest najbardziej prawdopodobna suma wyrzuconych oczek?

Rozważmy rzut sześcioma kostkami do gry, z których każda ma inny kolor. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że uzyskany wynik rzutu spełnia równocześnie trzy warunki:
– dokładnie na dwóch kostkach otrzymano po jednym oczku;
– dokładnie na trzech kostkach otrzymano po sześć oczek;
– suma wszystkich otrzymanych liczb oczek jest parzysta.

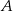Rzucamy trzy razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że co najmniej jeden raz wypadnie ścianka z dwoma oczkami.

Rzucamy 6 razy symetryczną 6-ścienną kostką do gry. Oblicz prawdopodobieństwo

otrzymania co najmniej raz szóstki;
otrzymania co najwyżej raz szóstki.

Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadną co najmniej dwa oczka.

Ukryj Podobne zadania

Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadnie liczba od 1 do 6.

Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadnie liczba pierwsza?

Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 3.

Ukryj Podobne zadania

Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 4.

Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 5.

Rzucamy trzykrotnie symetryczną kostką sześcienną do gry. Oblicz prawdopodobieństwa następujących zdarzeń:

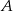– na każdej kostce wypadnie nieparzysta liczba oczek,
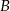– suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 3.

Rzucamy trzy razy symetryczną sześcienną kostką do gry. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwo, że w każdym rzucie liczba oczek będzie większa od numeru rzutu.

Oblicz prawdopodobieństwo otrzymania dokładnie dwóch jedynek lub trzech szóstek w doświadczeniu losowym, polegającym na pięciokrotnym rzucie symetryczną sześcienną kostką do gry.

Oblicz prawdopodobieństwo tego, że przy czterokrotnym rzucie kostką, 3 kolejne wyniki utworzą ciąg geometryczny.

Rzucamy czterokrotnie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy dokładnie dwie dwójki lub dokładnie dwie piątki. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

Rzucamy dwa razy symetryczną, sześcienną kostką, której jedna ściana ma jedno oczko, dwie ściany mają po dwa oczka i trzy ściany mają po trzy oczka. Oblicz prawdopodobieństwo zdarzenia: liczby oczek otrzymane w obu rzutach różnią się o 1.

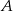Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 12. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.

Ukryj Podobne zadania

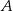Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego do sześciu oczek. Niech oznacza zdarzenie polegające na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach jest równy 12. Oblicz prawdopodobieństwo zdarzenia .

Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 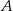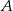polegającego na tym, że w pierwszym rzucie otrzymamy nieparzystą liczbę oczek i suma liczb oczek w obu rzutach będzie większa od 6. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.

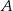Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach będzie podzielny przez 6.

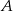Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie otrzymamy nieparzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 6.

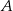Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 54.

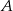Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.

Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia
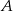– na każdej kostce wypadła nieparzysta liczba oczek,
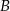– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia A ∪ B .

Gracz rzuca dwa razy symetryczną sześcienną kostką do gry i oblicza iloczyn wyrzucanych oczek. Jeśli iloczyn ten jest liczbą podzielną przez 2 lub przez 3 to przegrywa. W pozostałych przypadkach wygrywa.

Uzupełnij tabelkę tak, aby przedstawiała wszystkie wyniki tego doświadczenia.
Podaj liczbę wynikow sprzyjających wygranej gracza i oblicz prawdopodobieństwo wygranej.

Gracz rzuca dwa razy symetryczną sześcienną kostką do gry i oblicza sumę wyrzuconych oczek. Jeśli suma ta jest jedną z liczb: 6, 7 lub 8, to gracz wygrywa. W pozostałych przypadkach przegrywa.

Uzupełnij tabelę, tak aby przedstawiała wszystkie możliwe wyniki tego doświadczenia losowego.
Podaj liczbę wyników sprzyjających wygranej gracza i oblicz prawdopodobieństwo wygranej.

Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy sumę oczek równą 16.

Ukryj Podobne zadania

Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy sumę oczek równą 17.

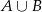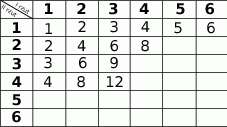
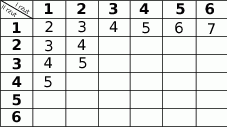
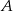Gracz rzuca raz sześcienną kostką z liczbami 2,4 i 9 na ściankach, a gracz 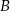rzuca raz kostką z liczbami 3,5 i 7 przy czym każda liczba znajduje się na dwóch ściankach kostki. Wygrywa ten gracz, na którego kostce wypadnie większa liczba. Oblicz prawdopodobieństwo wygrania gracza .

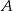Strona 2 z 3