Prawidłowy trójkątny/Ostrosłup - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny

Ostrosłup prawidłowy trójkątny przecięto płaszczyzną, która przechodzi przez krawędź podstawy długości oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem . Oblicz objętość ostrosłupa.

Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego jest równe 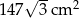√ -- 14 7 3 cm 2 , a pole jego powierzchni całkowitej wynosi 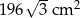√ -- 1 96 3 cm 2 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.

Podstawą ostrosłupa prawidłowego jest trójkąt równoboczny. Wysokość ściany bocznej tego ostrosłupa jest równa 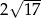√ --- 2 17 , a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa.

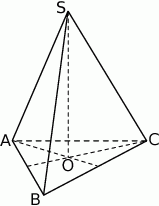
W ostrosłupie prawidłowym trójkątnym stosunek pola powierzchni bocznej do pola podstawy jest równe 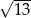√ --- 13 . Oblicz miarę kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy.

Ukryj Podobne zadania

W ostrosłupie prawidłowym trójkątnym 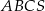ABCS pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.

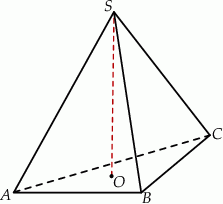
W ostrosłupie prawidłowym trójkątnym 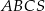ABCS krawędź podstawy ma długość . Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy.

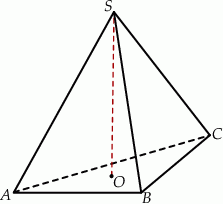
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 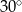30 ∘ . Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

Wysokość ostrosłupa prawidłowego trójkątnego jest równa 4, a krawędź podstawy ma długość 1. Ostrosłup przecięto płaszczyzną, która przechodzi przez krawędź podstawy oraz jest prostopadła do przeciwległej krawędzi bocznej. Oblicz pole powierzchni tego przekroju.

Krawędź podstawy ostrosłupa trójkątnego prawidłowego jest równa 6. Jego objętość jest równa 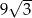√ -- 9 3 . Wyznacz długość wysokości ściany bocznej ostrosłupa.

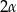W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość . Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa 2 α . Wyznacz objętość tego ostrosłupa.

Dany jest ostrosłup prawidłowy trójkątny. Promień okręgu opisanego na podstawie tego ostrosłupa jest równy 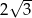√ -- 2 3 . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 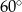60∘ . Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

Dany jest ostrosłup prawidłowy trójkątny 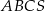ABCS o podstawie 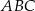ABC i polu powierzchni bocznej równym 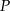. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 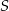ma miarę 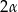. Objętość tego ostrosłupa jest równa 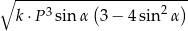∘ ----3------(--------2--) k ⋅P sin α 3− 4sin α , gdzie 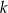jest stałym współczynnikiem liczbowym. Oblicz współczynnik .

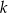W ostrosłupie prawidłowym trójkątnym krawędź boczna jest 2 razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta utworzonego przez dwie sąsiednie ściany boczne.

Ukryj Podobne zadania

W ostrosłupie prawidłowym trójkątnym krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta utworzonego przez dwie sąsiednie ściany boczne.

Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 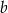i tworzy z płaszczyzną podstawy kąt o mierze . Jaką objętość ma ten ostrosłup?

W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 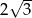√ -- 2 3 . Oblicz objętość tego ostrosłupa jeżeli kąt nachylenia krawędzi bocznej do podstawy ma miarę 60∘ .

Ukryj Podobne zadania

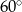W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 6. Oblicz objętość tego ostrosłupa jeżeli kąt nachylenia krawędzi bocznej do podstawy ma miarę 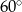60∘ .

W ostrosłupie prawidłowym trójkątnym 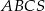ABCS o podstawie 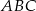ABC wysokość jest równa 3, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 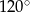12 0∘ . Oblicz objętość tego ostrosłupa.

Narożnik między dwiema ścianami i suﬁtem prostopadłościennego pokoju należy zamaskować trójkątnym fragmentem płyty gipsowo-kartonowej (patrz rysunek). Wiedząc, że 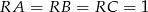RA = RB = RC = 1 m, oblicz objętość narożnika zamaskowanego tą płytą. Wynik zaokrąglij do 0,01 m 3 .

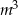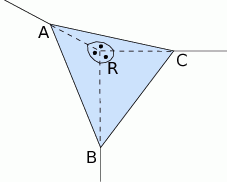
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest dwa razy dłuższa od krawędzi podstawy. Krawędź podstawy jest równa . Oblicz pole powierzchni bocznej i sinus połowy kąta między ścianami bocznymi ostrosłupa.

Podstawą ostrosłupa 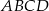ABCD jest trójkąt równoboczny 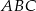ABC o boku długości 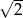√ -- 2 . Wszystkie ściany boczne są równoramiennymi trójkątami prostokątnymi. Punkt 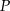został wybrany wewnątrz ostrosłupa w ten sposób, że wysokości ostrosłupów 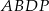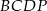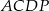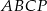ABDP , BCDP , ACDP , ABCP opuszczone z wierzchołka 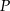mają tę samą długość 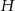. Sporządź rysunek ostrosłupa i oblicz .

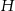Dany jest ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość i krawędź boczna jest od niej dwa razy dłuższa. Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa. Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej i oblicz pole tego przekroju.

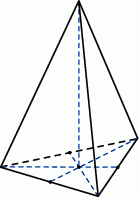
Objętość ostrosłupa prawidłowego trójkątnego 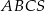ABCS jest równa 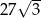√ -- 2 7 3 . Długość krawędzi 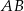podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.

Ukryj Podobne zadania

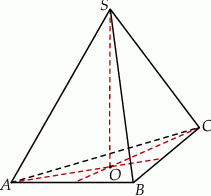
Objętość ostrosłupa prawidłowego trójkątnego 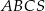ABCS jest równa 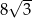√ -- 8 3 . Długość krawędzi 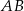podstawy ostrosłupa jest równa 4 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.

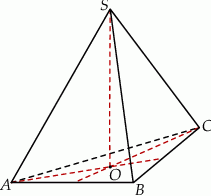
Trójkąt 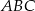ABC jest podstawą prawidłowego ostrosłupa 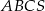ABCS , którego krawędź boczna ma długość 10. Punkt 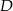jest środkiem wysokości 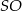ostrosłupa oraz 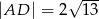√ --- |AD | = 2 13 . Oblicz objętość tego ostrosłupa.

Strona 2 z 3