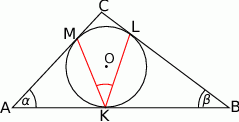
W okrąg wpisany jest trójkąt 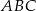 , przy czym
, przy czym 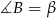 i
i 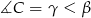 . Oblicz miarę kąta między prostą
. Oblicz miarę kąta między prostą 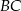 i styczną do okręgu w punkcie
i styczną do okręgu w punkcie 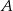 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny
Dane są długości boków  i
i 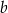 trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku
trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku 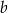 .
.
Na wysokości 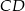 trójkąta
trójkąta 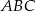 wybrano punkt
wybrano punkt 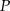 taki, że
taki, że 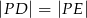 , gdzie
, gdzie 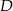 i
i 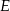 są rzutami tego punktu odpowiednio na boki
są rzutami tego punktu odpowiednio na boki 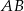 i
i 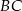 . Wiedząc, że
. Wiedząc, że 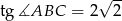 oblicz iloraz
oblicz iloraz  .
.
W okrąg o promieniu 4 wpisano trójkąt 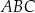 . Długość boku
. Długość boku 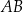 jest równa 6. Bok
jest równa 6. Bok 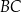 ma długość
ma długość 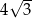 i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku
i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku 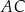 trójkąta
trójkąta 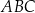 .
.
Wierzchołki 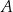 i
i 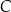 trójkąta
trójkąta 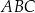 leżą na okręgu o promieniu
leżą na okręgu o promieniu  . Środek
. Środek 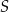 tego okręgu leży na boku
tego okręgu leży na boku 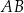 tego trójkąta (zobacz rysunek poniżej). Długości boków
tego trójkąta (zobacz rysunek poniżej). Długości boków 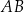 i
i 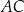 są równe odpowiednio
są równe odpowiednio 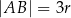 oraz
oraz 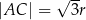 .
.
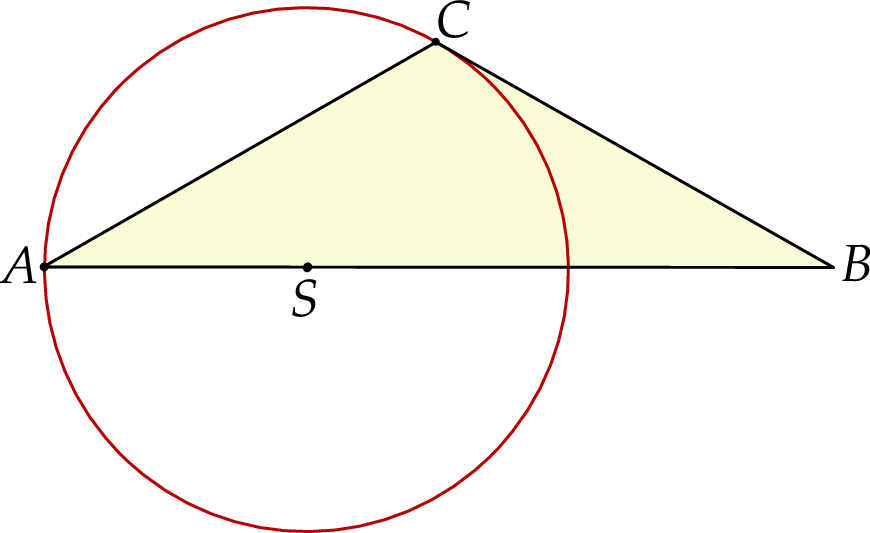
Oblicz miary wszystkich kątów wewnętrznych trójkąta 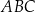 .
.
Udowodnij, że jeżeli w trójkącie dwa kąty nie są równe, to naprzeciw większego z nich leży dłuższy bok.
Wykaż, że pole trójkąta o bokach 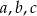 i promieniu
i promieniu 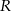 okręgu opisanego na nim jest równe
okręgu opisanego na nim jest równe 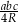 .
.
Wykaż, że pole trójkąta 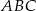 jest równe
jest równe 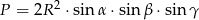 , gdzie
, gdzie 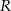 jest promieniem okręgu opisanego na tym trójkącie, a
jest promieniem okręgu opisanego na tym trójkącie, a 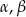 i
i 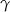 są miarami kątów wewnętrznych tego trójkąta.
są miarami kątów wewnętrznych tego trójkąta.
Długości boków trójkąta są w stosunku 2 : 3 : 4. Oblicz cosinus największego kąta tego trójkąta.
W trójkącie 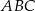 bok
bok 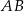 jest 3 razy dłuższy od boku
jest 3 razy dłuższy od boku 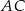 , a długość boku
, a długość boku 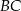 stanowi
stanowi  długości boku
długości boku 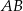 . Oblicz cosinus najmniejszego kąta trójkąta
. Oblicz cosinus najmniejszego kąta trójkąta 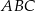 .
.
W trójkącie 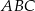 bok
bok 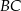 jest 3 razy krótszy od boku
jest 3 razy krótszy od boku 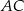 , a długość boku
, a długość boku 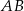 stanowi
stanowi  długości boku
długości boku 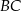 . Oblicz cosinus największego kąta trójkąta
. Oblicz cosinus największego kąta trójkąta 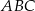 .
.
Dany jest trójkąt 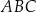 o bokach długości:
o bokach długości: 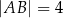 ,
, 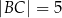 ,
, 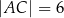 . Oblicz sinus najmniejszego kąta wewnętrznego trójkąta
. Oblicz sinus najmniejszego kąta wewnętrznego trójkąta 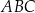 .
.
Dany jest trójkąt 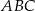 . Punkt
. Punkt 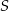 jest środkiem boku
jest środkiem boku 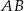 tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 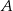 i
i 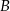 od prostej
od prostej 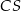 są równe.
są równe.
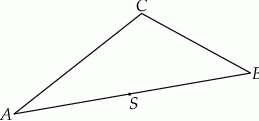
Na boku 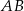 trójkąta
trójkąta 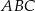 wybrano punkt
wybrano punkt 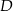 w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 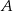 i
i 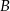 od prostej
od prostej 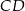 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 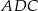 i
i 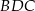 mają równe pola.
mają równe pola.
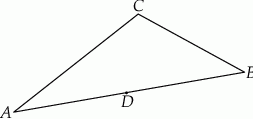
Miary dwóch kątów trójkąta wynoszą 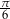 i
i 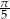 . Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
. Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
Na środkowej 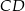 trójkąta
trójkąta 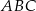 wybrano punkt
wybrano punkt 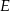 . Wykaż, że trójkąty
. Wykaż, że trójkąty 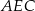 i
i 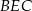 mają równe pola.
mają równe pola.
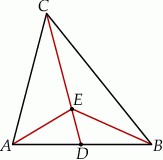
Odcinki 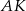 i
i 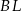 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 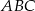 , a punkt
, a punkt 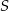 jest punktem ich przecięcia. Uzasadnij, że:
jest punktem ich przecięcia. Uzasadnij, że:
- na czworokącie
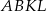 można opisać okrąg;
można opisać okrąg; - okręgi opisane na trójkątach
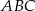 i
i 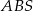 mają promienie równej długości.
mają promienie równej długości.
Obwód trójkąta 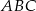 jest równy 8. Oblicz obwód trójkąta
jest równy 8. Oblicz obwód trójkąta 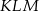 o wierzchołkach będących środkami środkowych trójkąta
o wierzchołkach będących środkami środkowych trójkąta 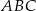 .
.
Pole trójkąta 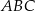 jest równe
jest równe 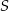 , a długości jego boków
, a długości jego boków 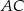 i
i 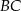 są odpowiednio równe
są odpowiednio równe 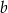 i
i  . Na bokach
. Na bokach 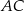 i
i 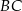 zbudowano kwadraty o środkach odpowiednio
zbudowano kwadraty o środkach odpowiednio 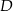 i
i 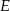 .
.
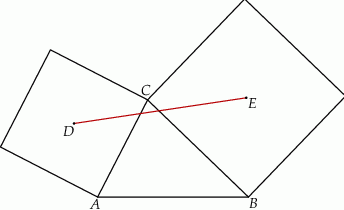
Wykaż, że
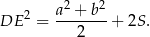
Wykaż, że jeżeli w trójkącie 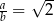 to
to 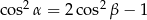 .
.
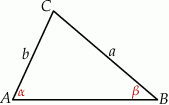
Dwusieczna kąta 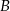 trójkąta
trójkąta 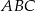 przecina bok
przecina bok 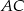 w punkcie
w punkcie 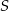 , a dwusieczna kąta
, a dwusieczna kąta 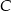 przecina bok
przecina bok 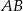 w punkcie
w punkcie 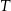 . Dwusieczne przecinają się w punkcie
. Dwusieczne przecinają się w punkcie 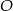 . Znajdź miarę kąta
. Znajdź miarę kąta 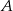 , jeżeli wiadomo, że na czworokącie
, jeżeli wiadomo, że na czworokącie 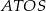 można opisać okrąg.
można opisać okrąg.
Boki trójkąta mają długości 4, 8 i 10.
- Oblicz cosinus i tangens kąta leżącego naprzeciwko najkrótszego boku.
- Oblicz długość środkowej poprowadzonej do najdłuższego boku.
Na bokach 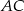 i
i 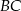 trójkąta
trójkąta 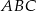 obrano punkty
obrano punkty 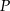 i
i 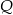 takie, że
takie, że 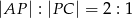 oraz
oraz 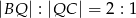 . Odcinki
. Odcinki 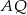 i
i 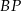 przecinają się w punkcie
przecinają się w punkcie 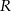 . Wykaż, że pole czworokąta
. Wykaż, że pole czworokąta 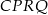 jest równe polu trójkąta
jest równe polu trójkąta 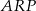 .
.
W trójkąt 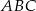 , w którym
, w którym 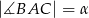 oraz
oraz 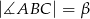 , wpisano okrąg. Punkty
, wpisano okrąg. Punkty 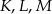 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 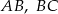 i
i 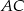 . Wykaż, że
. Wykaż, że 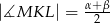 .
.