Inne/Stożek/Stereometria - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Stożek/Inne

Pole powierzchni bocznej stożka jest czterokrotnie większe od pola podstawy stożka. Oblicz wysokość stożka, wiedząc, że promień jego podstawy jest równy .

W stożku o promieniu podstawy tworząca jest nachylona do płaszczyzny podstawy pod kątem . Przez wierzchołek stożka poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod kątem β > α .

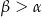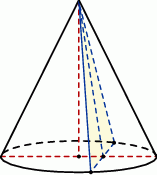
Wykaż, że pole otrzymanego przekroju stożka jest równe

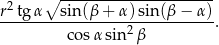
2 ∘ ---------------------- r-tg-α--sin(β-+-α-)sin(β-−-α)-. cos αsin2 β

Powierzchnia boczna stożka jest wycinkiem kołowym, którego kąt środkowy ma miarę 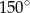15 0∘ . Wiedząc, że tworząca stożka ma długość 24 cm, oblicz pole powierzchni bocznej i objętość tego stożka.

Ukryj Podobne zadania

Powierzchnia boczna stożka jest wycinkiem kołowym, którego kąt środkowy ma miarę 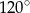12 0∘ . Wiedząc, że tworząca stożka ma długość 12 cm, oblicz pole powierzchni bocznej i objętość tego stożka.

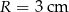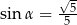Metalową kulę o promieniu R = 3 cm przetopiono na stożek. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem , takim, że √ - sinα = --5 5 . Wyznacz promień podstawy tego stożka.

Stożek ma wysokość 10 cm. Pole przekroju osiowego tego stożka jest równe 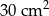30 cm 2 . Jaką długość ma tworząca tego stożka?

Powierzchnia boczna stożka jest po rozwinięciu ćwiartką koła o promieniu 16 cm. Oblicz pole powierzchni całkowitej i objętość tego stożka.

Ukryj Podobne zadania

Powierzchnia boczna stożka jest po rozwinięciu ćwiartką koła o promieniu 12 cm. Oblicz pole powierzchni całkowitej i objętość tego stożka.

Tworząca stożka ma długość 17, a wysokość stożka jest krótsza od średnicy jego podstawy o 22. Oblicz pole powierzchni całkowitej i objętość tego stożka.

Ukryj Podobne zadania

Tworząca stożka ma długość 25, a średnica podstawy stożka jest krótsza od wysokości stożka o 10. Oblicz pole powierzchni całkowitej i objętość tego stożka.

Połówkę koła o promieniu 12 zwinięto w stożek. Oblicz objętość i kąt rozwarcia tego stożka jeżeli długość łuku tej połówki koła jest obwodem podstawy, a jej promień jest tworzącą stożka.

W stożek o promieniu podstawy długości 9 i wysokości 12 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz długość promienia podstawy i długość wysokości walca, wiedząc że pole powierzchni bocznej walca wynosi 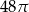48π .

Ukryj Podobne zadania

W stożek o promieniu podstawy długości 10 i wysokości 15 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz długość promienia podstawy i długość wysokości walca, wiedząc że pole powierzchni bocznej walca wynosi 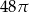48π .

Objętość stożka jest równa 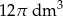3 12π dm , a cosinus kąta między wysokością, a tworzącą wynosi 0,8. Oblicz:

pole powierzchni bocznej stożka;
miarę kąta środkowego powierzchni bocznej stożka po rozwinięciu na płaszczyźnie.

W stożek o promieniu podstawy długości 6 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz promień podstawy walca, jeżeli jego objętość stanowi 4 9 objętości stożka.

Tomek i Marek chcą wejść docelowo na szczyt 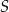pewnej góry. W chwili początkowej znajdują się w punkcie 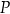położonym na stoku góry dokładnie na północ od szczytu na wysokości 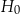metrów n.p.m. Tomek i Marek chcą dotrzeć do bazy 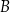znajdującej się dokładnie na południe od szczytu na przeciwległym południowym stoku góry na wysokości 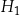H 1 metrów n.p.m., a następnie z bazy wejść na szczyt leżący na wysokości 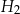H 2 metrów n.p.m. (zobacz rysunek).

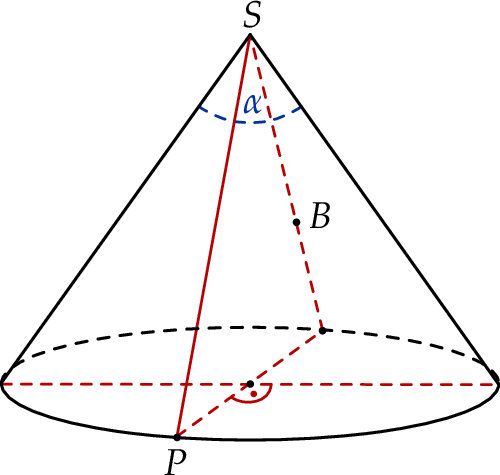
ZINFO-FIGURE

Oblicz długość najkrótszej drogi, jaką muszą pokonać, aby dotrzeć do bazy. Przyjmij, że góra jest stożkiem o kącie rozwarcia .

Czy kwadratową płytą o boku długości 2,2 m można całkowicie zakryć otwór w ziemi, który ma kształt stożka o wysokości 2 m i kącie rozwarcia 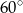60∘ ?

Odpowiedź uzasadnij.

Do naczynia w kształcie odwróconego stożka wrzucono kulkę o promieniu 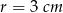r = 3 cm . Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.