Dane jest równanie 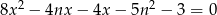 z niewiadomą
z niewiadomą  i parametrem
i parametrem  .
.
- Wyznacz wszystkie wartości
 , dla których suma odwrotności pierwiastków tego równania jest równa
, dla których suma odwrotności pierwiastków tego równania jest równa 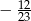 .
. - Wykaż, że jeżeli
 jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.

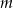 , dla których prosta
, dla których prosta 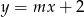 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 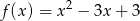 .
. 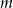 , dla których prosta
, dla których prosta 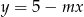 ma dwa punkty wspólne z wykresem funkcji
ma dwa punkty wspólne z wykresem funkcji 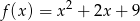 .
. 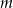 , dla których prosta
, dla których prosta 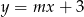 ma dwa punkty wspólne z wykresem funkcji
ma dwa punkty wspólne z wykresem funkcji 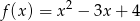 .
. 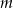 , dla których prosta
, dla których prosta 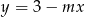 ma jeden punkt wspólny z wykresem funkcji
ma jeden punkt wspólny z wykresem funkcji 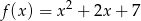 .
. 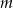 , dla których prosta
, dla których prosta 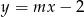 ma jeden punkt wspólny z wykresem funkcji
ma jeden punkt wspólny z wykresem funkcji 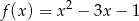 .
. 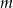 , dla których prosta
, dla których prosta 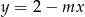 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 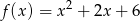 .
. 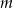 suma pierwiastków równania
suma pierwiastków równania 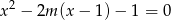 jest równa sumie kwadratów tych pierwiastków?
jest równa sumie kwadratów tych pierwiastków? 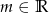 , dla których równanie
, dla których równanie 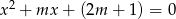 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 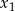 i
i 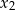 takie, że
takie, że 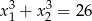 .
. 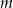 , dla których równanie
, dla których równanie 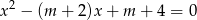 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 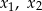 takie, że
takie, że 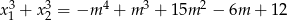 .
. 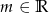 , dla których równanie
, dla których równanie 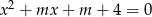 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 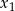 i
i 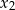 takie, że
takie, że 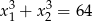 .
. 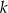 , dla której suma kwadratów dwóch różnych pierwiastków równania
, dla której suma kwadratów dwóch różnych pierwiastków równania 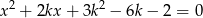 jest największa z możliwych.
jest największa z możliwych. 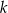 suma kwadratów pierwiastków równania
suma kwadratów pierwiastków równania 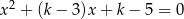 jest najmniejsza?
jest najmniejsza? 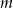 suma kwadratów dwóch różnych pierwiastków równania
suma kwadratów dwóch różnych pierwiastków równania 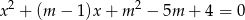 przyjmuje wartość największą. Wyznacz tę wartość.
przyjmuje wartość największą. Wyznacz tę wartość. 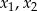 są takimi rozwiązaniami równania
są takimi rozwiązaniami równania 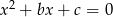
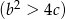 , że
, że 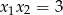 i
i 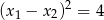 . Oblicz
. Oblicz 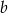 i
i  .
. 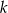 , dla których równanie
, dla których równanie 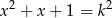 ma pierwiastki będące liczbami całkowitymi.
ma pierwiastki będące liczbami całkowitymi. 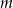 równanie
równanie 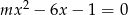 ma co najmniej jedno rozwiązanie?
ma co najmniej jedno rozwiązanie? 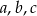 takie, że równanie
takie, że równanie 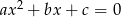 ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.
ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną. 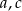 takie, że funkcja
takie, że funkcja 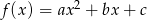 ma miejsce zerowe będące liczbą wymierną. Wykaż, że
ma miejsce zerowe będące liczbą wymierną. Wykaż, że 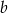 jest liczbą wymierną.
jest liczbą wymierną. 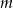 równanie
równanie 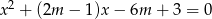 ma dwa różne pierwiastki
ma dwa różne pierwiastki 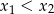 spełniające nierówność
spełniające nierówność 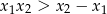 .
. 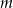 , dla których równanie
, dla których równanie 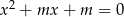 ma takie dwa różne pierwiastki, że suma ich kwadratów jest mniejsza od 15.
ma takie dwa różne pierwiastki, że suma ich kwadratów jest mniejsza od 15. 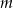 , dla których równanie
, dla których równanie 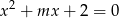 ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest większa od
ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest większa od 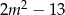 .
. 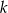 , dla których dane równanie ma dwa różne pierwiastki
, dla których dane równanie ma dwa różne pierwiastki 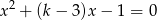 .
. 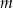 , dla których równanie
, dla których równanie 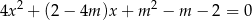
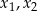 spełniające nierówność
spełniające nierówność 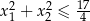 .
. 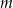 , dla których równanie
, dla których równanie 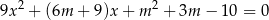
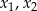 spełniające nierówność
spełniające nierówność 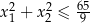 .
. 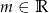 równanie
równanie 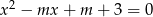 ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 1?
ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 1? 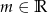 , dla których równanie
, dla których równanie 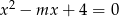 ma dwa różne pierwiastki spełniające nierówność
ma dwa różne pierwiastki spełniające nierówność 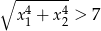 .
. 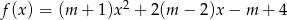 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 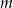 , dla których trójmian
, dla których trójmian 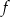 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 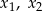 , spełniające warunek
, spełniające warunek 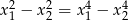 .
. 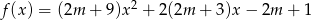 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 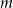 , dla których trójmian
, dla których trójmian 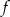 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 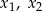 , spełniające warunek
, spełniające warunek 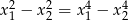 .
. 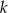 , dla których równanie
, dla których równanie 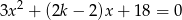
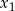 i
i 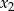 , przy czym
, przy czym 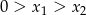 , spełniające warunek
, spełniające warunek 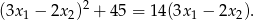
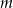 liczba 1 zawiera się między różnymi pierwiastkami równania
liczba 1 zawiera się między różnymi pierwiastkami równania 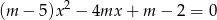 ?
?  , dla których równanie
, dla których równanie 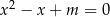 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 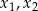 spełniające warunek
spełniające warunek 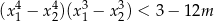 .
. 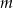 i
i  są takimi liczbami całkowitymi, że rozwiązania równania
są takimi liczbami całkowitymi, że rozwiązania równania 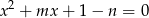 są niezerowymi liczbami całkowitymi, to liczba
są niezerowymi liczbami całkowitymi, to liczba 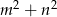 nie jest liczbą pierwszą.
nie jest liczbą pierwszą. 