Wyznacz wszystkie wartości parametru 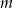 , dla których równanie
, dla których równanie
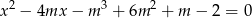
ma dwa różne pierwiastki rzeczywiste 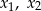 takie, że
takie, że 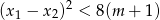 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie wartości parametru 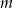 , dla których równanie
, dla których równanie
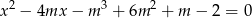
ma dwa różne pierwiastki rzeczywiste 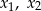 takie, że
takie, że 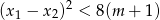 .
.
Wyznacz wszystkie wartości parametru 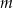 , dla których funkcja kwadratowa
, dla których funkcja kwadratowa 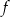 określona wzorem
określona wzorem
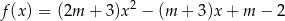
ma dwa różne pierwiastki rzeczywiste 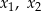 spełniające warunek
spełniające warunek 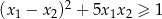 .
.
Wyznacz wszystkie wartości parametru 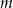 , dla których funkcja kwadratowa
, dla których funkcja kwadratowa 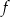 określona wzorem
określona wzorem
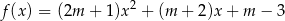
ma dwa różne pierwiastki rzeczywiste 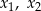 spełniające warunek
spełniające warunek 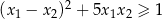 .
.
Dla jakich wartości parametru 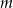 , odwrotność sumy pierwiastków równania
, odwrotność sumy pierwiastków równania
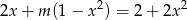
jest dodatnia?
Miejscami zerowymi trójmianu 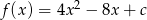 , są liczby całkowite dodatnie. Oblicz
, są liczby całkowite dodatnie. Oblicz  .
.
Wyznacz wszystkie wartości parametru 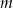 , dla których równanie
, dla których równanie
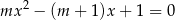
ma dwa różne rozwiązania rzeczywiste 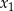 oraz
oraz 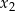 , spełniające warunek:
, spełniające warunek:
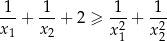
Wyznacz wszystkie wartości parametru 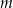 , dla których równanie
, dla których równanie
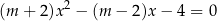
ma dwa różne rozwiązania rzeczywiste 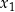 oraz
oraz 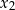 , spełniające warunek:
, spełniające warunek:
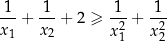
Wyznacz wszystkie wartości parametru 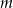 , dla których równanie
, dla których równanie 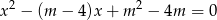 ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od
ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od 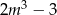 .
.
Wyznacz współczynniki 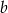 i
i  trójmianu kwadratowego
trójmianu kwadratowego 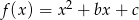 , wiedząc że jego miejsca zerowe
, wiedząc że jego miejsca zerowe 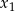 i
i 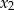 spełniają warunek:
spełniają warunek: 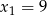 i
i 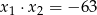 .
.
Dane jest równanie 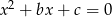 z niewiadomą
z niewiadomą  . Wyznacz wartości
. Wyznacz wartości 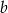 i
i  tak, by były one rozwiązaniami danego równania.
tak, by były one rozwiązaniami danego równania.
Różnymi pierwiastkami równania kwadratowego 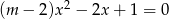 są liczby
są liczby 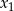 oraz
oraz 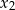 . Narysuj wykres funkcji
. Narysuj wykres funkcji 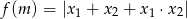 .
.
Punkt 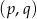 należy do zbioru
należy do zbioru 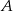 wtedy i tylko wtedy, gdy równanie
wtedy i tylko wtedy, gdy równanie 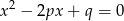 ma dwa różne rozwiązania
ma dwa różne rozwiązania 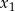 i
i 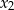 takie, że
takie, że 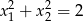 . Zaznacz w układzie współrzędnych zbiór
. Zaznacz w układzie współrzędnych zbiór 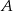 .
.
Wyznacz wszystkie liczby całkowite 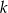 , dla których iloczyn dwóch różnych miejsc zerowych funkcji
, dla których iloczyn dwóch różnych miejsc zerowych funkcji 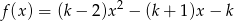 jest liczbą całkowitą.
jest liczbą całkowitą.
Dane jest równanie 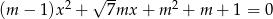 z niewiadomą
z niewiadomą  . Sporządź wykres funkcji
. Sporządź wykres funkcji 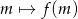 , gdzie
, gdzie 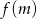 oznacza liczbę rzeczywistych pierwiastków danego równania.
oznacza liczbę rzeczywistych pierwiastków danego równania.
Wyznacz dziedzinę i naszkicuj wykres funkcji 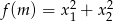 , gdzie
, gdzie 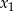 i
i 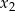 są różnymi pierwiastkami równania
są różnymi pierwiastkami równania 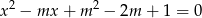 .
.
Oblicz wszystkie wartości parametru 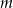 , dla których równanie
, dla których równanie 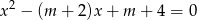 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 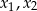 takie, że
takie, że 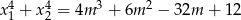 .
.
Wyznacz te wartości parametru 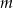 , dla których równanie
, dla których równanie 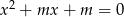 ma dwa różne pierwiastki takie, że ich iloczyn jest mniejszy od 6.
ma dwa różne pierwiastki takie, że ich iloczyn jest mniejszy od 6.
Dla jakich wartości parametru 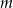 każdy z dwóch różnych pierwiastków równania
każdy z dwóch różnych pierwiastków równania 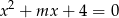 jest mniejszy od 4?
jest mniejszy od 4?
Znajdź te wartości parametru 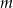 dla których funkcja
dla których funkcja 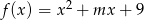 ma dwa miejsca zerowe większe od 2.
ma dwa miejsca zerowe większe od 2.
Dla jakich wartości parametru 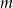 równanie
równanie 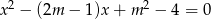 ma dwa różne pierwiastki rzeczywiste mniejsze od 4?
ma dwa różne pierwiastki rzeczywiste mniejsze od 4?
Wyznacz te wartości parametru 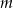 , dla których równanie
, dla których równanie 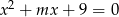 ma dwa rozwiązania mniejsze od
ma dwa rozwiązania mniejsze od 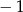 .
.
Wyznacz wszystkie wartości parametru 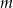 , dla których równanie
, dla których równanie 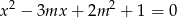 ma dwa różne rozwiązania takie, że każde należy do przedziału
ma dwa różne rozwiązania takie, że każde należy do przedziału 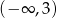 .
.
Wyznacz wszystkie wartości parametru 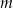 , dla których oba pierwiastki równania
, dla których oba pierwiastki równania
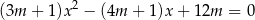
są większe od 2.
Wyznacz wszystkie wartości parametru 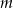 , dla których równanie
, dla których równanie
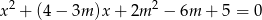
ma dwa różne rozwiązania takie, że każde należy do przedziału 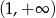 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 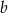 i
i  , funkcja
, funkcja
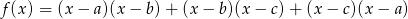
ma co najmniej jedno miejsce zerowe.
Dla jakich wartości parametru 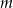 równanie
równanie 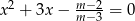 ma dwa pierwiastki rzeczywiste? Wyznacz te wartości parametru
ma dwa pierwiastki rzeczywiste? Wyznacz te wartości parametru 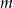 , dla których suma sześcianów pierwiastków tego równania jest równa -9.
, dla których suma sześcianów pierwiastków tego równania jest równa -9.
Dla jakich wartości parametru 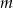 równanie
równanie 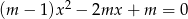 posiada 2 różne rozwiązania?
posiada 2 różne rozwiązania?
Dla jakich wartości parametru 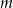 równanie
równanie 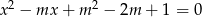 ma dwa różne pierwiastki rzeczywiste, których suma jest o jeden większa od ich iloczynu?
ma dwa różne pierwiastki rzeczywiste, których suma jest o jeden większa od ich iloczynu?
Dane jest równanie 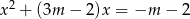 z niewiadomą
z niewiadomą  . Sformułuj warunki, jakie powinien spełniać parametr
. Sformułuj warunki, jakie powinien spełniać parametr 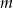 , by to równanie miało dwa różne pierwiastki, których suma odwrotności jest dodatnia.
, by to równanie miało dwa różne pierwiastki, których suma odwrotności jest dodatnia.
