Punkt 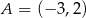 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 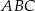 , w którym
, w którym 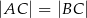 . Pole tego trójkąta jest równe 15. Bok
. Pole tego trójkąta jest równe 15. Bok 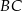 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 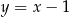 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 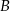 i
i 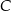 tego trójkąta.
tego trójkąta.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny
Punkt 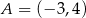 jest wierzchołkiem rozwartokątnego trójkąta równoramiennego
jest wierzchołkiem rozwartokątnego trójkąta równoramiennego 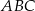 , w którym
, w którym 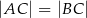 . Pole tego trójkąta jest równe 17,5 i wszystkie jego wierzchołki mają współrzędne całkowite. Bok
. Pole tego trójkąta jest równe 17,5 i wszystkie jego wierzchołki mają współrzędne całkowite. Bok 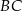 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 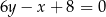 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 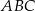 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 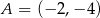 oraz
oraz 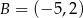 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 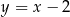 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Podstawą trójkąta równoramiennego 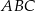 jest bok
jest bok 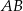 , gdzie
, gdzie 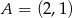 i
i 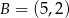 . Ramię tego trójkąta zawiera się w prostej o równaniu
. Ramię tego trójkąta zawiera się w prostej o równaniu 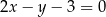 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 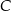 .
.
Dany jest trójkąt równoramienny 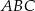 , w którym
, w którym 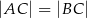 . Ponadto wiadomo, że
. Ponadto wiadomo, że 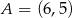 i
i 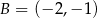 . Wierzchołek
. Wierzchołek 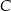 należy do osi
należy do osi 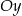 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 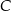 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 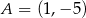 oraz
oraz 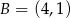 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 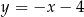 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Punkt 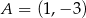 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 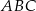 , w którym
, w którym 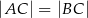 . Punkt
. Punkt 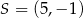 jest środkiem odcinka
jest środkiem odcinka 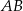 . Wierzchołek
. Wierzchołek 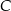 tego trójkąta leży na prostej o równaniu
tego trójkąta leży na prostej o równaniu 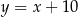 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 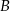 i
i 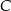 tego trójkąta.
tego trójkąta.
Dany jest trójkąt równoramienny 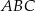 , w którym
, w którym 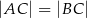 . Ponadto wiadomo, że
. Ponadto wiadomo, że 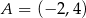 i
i 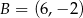 . Wierzchołek
. Wierzchołek 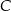 należy do osi
należy do osi 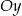 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 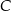 .
.
Podstawą trójkąta równoramiennego 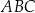 jest odcinek o końcach w punktach
jest odcinek o końcach w punktach 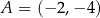 oraz
oraz 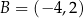 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 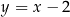 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 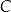 .
.
Punkty 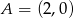 i
i 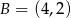 leżą na okręgu o równaniu
leżą na okręgu o równaniu 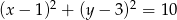 . Wyznacz na tym okręgu taki punkt
. Wyznacz na tym okręgu taki punkt 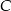 , aby trójkąt
, aby trójkąt 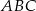 był trójkątem równoramiennym o podstawie
był trójkątem równoramiennym o podstawie 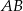 .
.
Ostrokątny trójkąt równoramienny 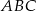 o podstawie
o podstawie 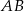 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 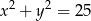 . Punkty
. Punkty 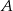 i
i 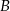 leżą na prostej o równaniu
leżą na prostej o równaniu 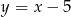 .
.
- Oblicz współrzędne punktów:
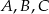 .
. - Oblicz kąty trójkąta
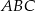 .
.

