Podstawa 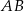 trójkąta równoramiennego
trójkąta równoramiennego 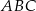 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 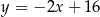 . Wierzchołki
. Wierzchołki 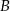 i
i 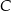 mają współrzędne
mają współrzędne 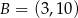 i
i 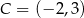 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 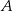 i pole trójkąta
i pole trójkąta 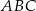 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny
Podstawa 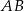 trójkąta równoramiennego
trójkąta równoramiennego 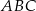 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 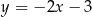 . Wierzchołki
. Wierzchołki 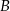 i
i 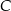 mają współrzędne
mają współrzędne 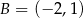 i
i 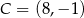 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 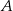 i pole trójkąta
i pole trójkąta 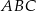 .
.
Punkt 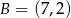 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 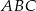 o podstawie
o podstawie 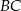 . Pole tego trójkąta jest równe 20, a wysokość poprowadzona z wierzchołka
. Pole tego trójkąta jest równe 20, a wysokość poprowadzona z wierzchołka 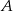 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 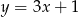 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 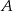 i
i 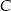 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.
Dany jest trójkąt równoramienny 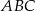 , w którym
, w którym 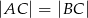 oraz
oraz 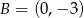 i
i 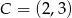 . Oś symetrii tego trójkąta ma równanie
. Oś symetrii tego trójkąta ma równanie 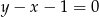 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 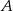 .
.
Punkty 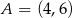 i
i 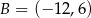 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 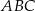 , w którym
, w którym 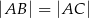 . Wysokość
. Wysokość 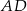 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 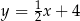 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 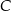 tego trójkąta.
tego trójkąta.
Punkty 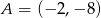 i
i 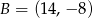 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 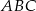 , w którym
, w którym 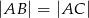 . Wysokość
. Wysokość 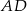 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 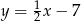 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 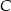 tego trójkąta.
tego trójkąta.
Punkty 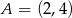 i
i 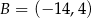 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 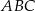 , w którym
, w którym 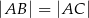 . Wysokość
. Wysokość 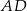 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 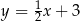 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 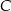 tego trójkąta.
tego trójkąta.
Punkty 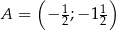 ,
, 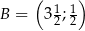 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 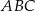 o podstawie
o podstawie 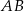 . Ramię
. Ramię 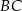 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 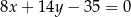 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 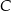 i pole tego trójkąta.
i pole tego trójkąta.
W równoramiennym trójkącie prostokątnym punkt 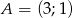 jest wierzchołkiem kąta ostrego. Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu
jest wierzchołkiem kąta ostrego. Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu 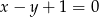 . Napisz równania prostych zawierających pozostałe boki trójkąta.
. Napisz równania prostych zawierających pozostałe boki trójkąta.
Dany jest trójkąt równoramienny 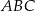 , w którym
, w którym 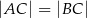 oraz
oraz 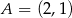 i
i 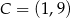 . Podstawa
. Podstawa 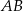 tego trójkąta jest zawarta w prostej
tego trójkąta jest zawarta w prostej 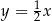 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 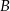 .
.
Punkty 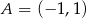 i
i 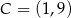 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 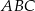 , w którym
, w którym 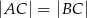 . Podstawa
. Podstawa 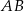 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 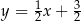 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 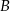 tego trójkąta.
tego trójkąta.
W układzie współrzędnych na płaszczyźnie zaznaczono punkty 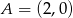 i
i 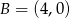 . Wyznacz wszystkie możliwe położenia punktu
. Wyznacz wszystkie możliwe położenia punktu 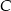 , dla których
, dla których 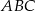 jest trójkątem równoramiennym o podstawie
jest trójkątem równoramiennym o podstawie 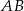 i polu równym 3.
i polu równym 3.
Punkty 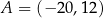 i
i 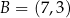 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 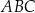 , w którym
, w którym 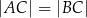 . Wierzchołek
. Wierzchołek 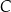 leży na osi
leży na osi 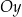 układu współrzędnych. Oblicz współrzędne wierzchołka
układu współrzędnych. Oblicz współrzędne wierzchołka 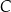 oraz obwód tego trójkąta.
oraz obwód tego trójkąta.
Punkty 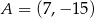 i
i 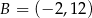 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 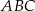 , w którym
, w którym 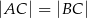 . Wierzchołek
. Wierzchołek 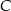 leży na prostej
leży na prostej 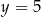 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 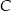 oraz obwód tego trójkąta.
oraz obwód tego trójkąta.
W kartezjańskim układzie współrzędnych 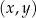 punkty
punkty 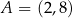 oraz
oraz 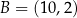 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 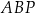 , w którym
, w którym 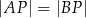 . Wierzchołek
. Wierzchołek 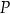 leży na osi
leży na osi 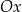 układu współrzędnych. Oblicz współrzędne punktu
układu współrzędnych. Oblicz współrzędne punktu 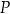 oraz długość odcinka
oraz długość odcinka 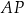 .
.
Punkty 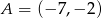 i
i 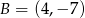 są wierzchołkami podstawy trójkąta równoramiennego
są wierzchołkami podstawy trójkąta równoramiennego 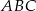 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 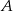 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 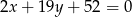 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 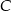 .
.
Punkty 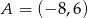 i
i 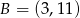 są wierzchołkami podstawy trójkąta równoramiennego
są wierzchołkami podstawy trójkąta równoramiennego 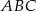 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 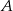 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 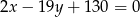 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 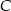 .
.
Podstawa trójkąta równoramiennego zawiera się w prostej 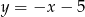 , a jedno z jego ramion w prostej
, a jedno z jego ramion w prostej 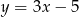 . Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych
. Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych 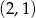 .
.
Podstawa 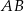 trójkąta równoramiennego
trójkąta równoramiennego 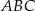 zawarta jest w prostej
zawarta jest w prostej 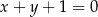 . Ramię
. Ramię 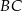 zawiera się w prostej
zawiera się w prostej 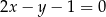 . Wyznacz równanie prostej
. Wyznacz równanie prostej 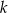 , zawierającej ramię
, zawierającej ramię 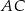 , wiedząc że punkt
, wiedząc że punkt 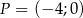 należy do prostej
należy do prostej 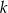 .
.
Punkt 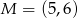 jest środkiem ramienia
jest środkiem ramienia 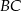 trójkąta równoramiennego
trójkąta równoramiennego 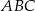 , w którym
, w którym 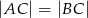 . Podstawa
. Podstawa  tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 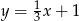 oraz
oraz 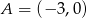 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 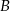 tego trójkąta.
tego trójkąta.
Punkt 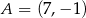 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 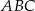 , w którym
, w którym 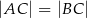 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 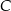 są liczbami ujemnymi. Okrąg wpisany w trójkąt
są liczbami ujemnymi. Okrąg wpisany w trójkąt 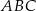 ma równanie
ma równanie 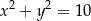 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 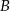 i
i 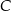 tego trójkąta.
tego trójkąta.
Punkt 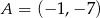 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 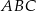 , w którym
, w którym 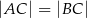 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 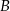 są liczbami dodatnimi. Okrąg wpisany w trójkąt
są liczbami dodatnimi. Okrąg wpisany w trójkąt 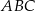 ma równanie
ma równanie 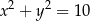 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 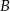 i
i 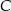 tego trójkąta.
tego trójkąta.
Punkty 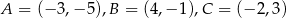 są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
Punkty 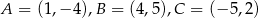 są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
Punkt 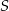 jest punktem przecięcia się środkowych trójkąta równoramiennego
jest punktem przecięcia się środkowych trójkąta równoramiennego 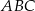 o podstawie
o podstawie 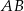 . Okrąg o średnicy
. Okrąg o średnicy 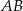 ma równanie
ma równanie 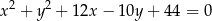 , a cięciwa tego okręgu równoległa do prostej
, a cięciwa tego okręgu równoległa do prostej 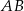 i przechodząca przez punkt
i przechodząca przez punkt 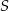 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 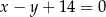 . Wyznacz równanie okręgu o środku
. Wyznacz równanie okręgu o środku 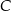 , który przechodzi przez punkty
, który przechodzi przez punkty 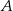 i
i 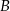 .
.
Punkty 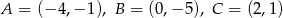 są wierzchołkami trójkąta równoramiennego. Wyznacz równanie osi symetrii tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Wyznacz równanie osi symetrii tego trójkąta.
Wyznacz równanie osi symetrii trójkąta o wierzchołkach 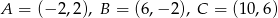 .
.
Wyznacz równanie osi symetrii trójkąta o wierzchołkach 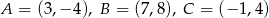 .
.
W trójkącie równoramiennym 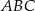 dane są wierzchołki podstawy:
dane są wierzchołki podstawy: 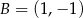 i
i 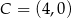 . Jedno z ramion trójkąta zawiera się w prostej o równaniu
. Jedno z ramion trójkąta zawiera się w prostej o równaniu 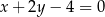 . Na boku
. Na boku 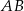 tego trójkąta obrano taki punkt
tego trójkąta obrano taki punkt 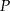 , że
, że 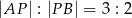 . Napisz równanie okręgu o środku w punkcie
. Napisz równanie okręgu o środku w punkcie 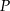 , stycznego do podstawy
, stycznego do podstawy 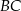 .
.
Punkty 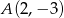 i
i 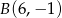 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 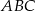 , którego pole jest równe 10. Wyznacz współrzędne wierzchołka
, którego pole jest równe 10. Wyznacz współrzędne wierzchołka 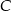 .
.
Odcinek 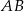 , gdzie
, gdzie 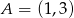 i
i 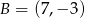 , jest podstawą trójkąta
, jest podstawą trójkąta 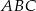 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 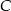 tak, aby trójkąt
tak, aby trójkąt 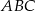 był równoramienny, a jego pole było równe 30.
był równoramienny, a jego pole było równe 30.
Punkt 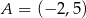 jest jednym z wierzchołków trójkąta równoramiennego
jest jednym z wierzchołków trójkąta równoramiennego 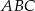 , w którym
, w którym 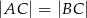 . Pole tego trójkąta jest równe 15. Bok
. Pole tego trójkąta jest równe 15. Bok 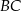 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 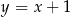 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 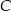 .
.
W trójkącie równoramiennym 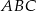 o podstawie
o podstawie 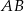 poprowadzono wysokość z wierzchołka
poprowadzono wysokość z wierzchołka 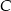 . Wyznacz równanie prostej zawierającej tę wysokość, jeśli
. Wyznacz równanie prostej zawierającej tę wysokość, jeśli 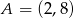 ,
, 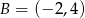 .
.

