Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Najmniejsze pole

Wyszukiwanie zadań

Podstawą prostopadłościanu jest prostokąt o stosunku boków 1:3. Objętość bryły jest równa 12. Oblicz wymiary tego prostopadłościanu, aby jego powierzchnia całkowita była najmniejsza. Oblicz tę najmniejszą powierzchnię.

Rozważamy wszystkie walce o objętości 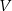V . Wyznacz wysokość i promień podstawy tego z rozważanych walców, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to pole.

Zakład produkcyjny planuje wytwarzanie pojemników o objętości 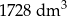3 1728 dm , które mają kształt otwartego graniastosłupa prawidłowego czworokątnego (bez górnej podstawy – zobacz rysunek).

PIC

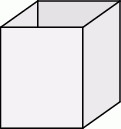
Koszt produkcji 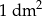2 1 dm podstawy tego pojemnika wynosi 0,3 zł, a koszt produkcji 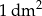1 dm 2 jego ścian bocznych wynosi 0,2 zł. Ponadto, do kosztu produkcji należy doliczyć niezbędne wzmocnienie krawędzi podstawy w cenie 4,2 zł za 1 dm długości. Oblicz jakie powinny być wymiary tego pojemnika tak, aby koszt jego produkcji był najmniejszy możliwy.

Firma logistyczna planuje produkcję pojemników w kształcie graniastosłupa prostego o objętości 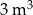3 m 3 i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za 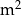m 2 , a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za 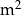2 m . Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.

Rozpatrujemy wszystkie prostopadłościany o objętości 8, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:2 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 28. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.

Ukryj Podobne zadania

Rozpatrujemy wszystkie prostopadłościany o objętości 27, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:3 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 52. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.

Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności 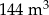144 m 3 . Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– 100 zł za 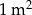2 1 m dna
– 75 zł za 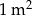1 m 2 ściany bocznej.
Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.

Ukryj Podobne zadania

Zakład produkcyjny dostał zlecenie produkcji prostopadłościennych pudełek (całkowicie otwartych od góry) o objętości 60,75 litra. Dno pudełka ma być kwadratem i żaden z jego wymiarów nie może przekraczać 67,5 cm. Na koszt wykonania pudełka składają się – koszt wykonania 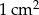1 cm 2 dna w wysokości 48 gorszy oraz koszt wykonania 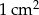2 1 cm ściany bocznej w wysokości 36 groszy. Oblicz wymiary pudełka, dla których koszt jego produkcji będzie najmniejszy.

Rozważmy wszystkie graniastosłupy prawidłowe trójkątne o objętości 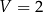V = 2 . Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.

Ukryj Podobne zadania

Rozważmy wszystkie graniastosłupy prawidłowe czworokątne o objętości 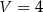V = 4 . Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.

Rozważamy wszystkie graniastosłupy prawidłowe trójkątne o objętości 3456, których krawędź podstawy ma długość nie większą niż 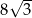√ -- 8 3 .

  • Wykaż, że pole 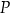P powierzchni całkowitej graniastosłupa w zależności od długości a krawędzi podstawy graniastosłupa jest określone wzorem

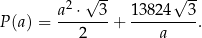
    √ -- √ -- a2-⋅--3 138-24--3 P (a) = 2 + a .

  • Wyznacz długość krawędzi podstawy tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.

Puszka konserwy ma kształt walca. Jaką wysokość i jaki promień podstawy powinna mieć ta puszka, aby przy objętości puszki 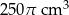250π cm 3 zużyć jak najmniej materiału na jej wykonanie.