Wykaż, że równanie 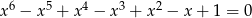 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
/Szkoła średnia/Równania/Wielomianowe/Różne
Znajdź wielomian o współczynnikach całkowitych, którego pierwiastkiem jest liczba 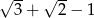 .
.
Funkcja 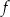 jest określona wzorem
jest określona wzorem 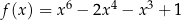 dla każdego
dla każdego 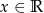 . Wykaż, że liczba 5 należy do zbioru wartości tej funkcji.
. Wykaż, że liczba 5 należy do zbioru wartości tej funkcji.
Rozwiąż równanie 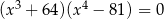 .
.
Rozwiąż równanie 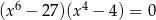 .
.
Rozwiąż równanie 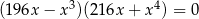 .
.
Uzasadnij, że jeżeli współczynniki wielomianu 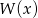 są liczbami całkowitymi i
są liczbami całkowitymi i 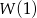 jest liczbą nieparzystą, to liczba nieparzysta nie jest pierwiastkiem wielomianu
jest liczbą nieparzystą, to liczba nieparzysta nie jest pierwiastkiem wielomianu 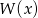 .
.
Dany jest wielomian 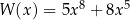 określony dla dowolnej liczby rzeczywistej
określony dla dowolnej liczby rzeczywistej  . Wykaż, równanie
. Wykaż, równanie 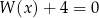 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Rozwiąż równanie 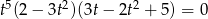 .
.
Rozwiąż równanie 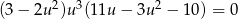 .
.
Rozwiąż równanie 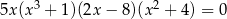 .
.
Rozwiąż równanie 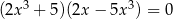 .
.
Wykaż, że równanie 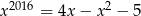 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Rozwiąż równanie 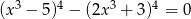 .
.
Rozwiąż równanie 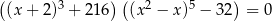 .
.
Wykaż, że jeżeli pierwiastkiem wielomianu
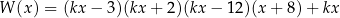
jest liczba całkowita podzielna przez 5, to 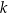 nie jest liczbą całkowitą.
nie jest liczbą całkowitą.
Wykaż, że równanie 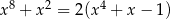 ma tylko jedno rozwiązanie rzeczywiste
ma tylko jedno rozwiązanie rzeczywiste 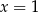 .
.
Wykaż, że równanie 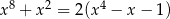 ma tylko jedno rozwiązanie rzeczywiste
ma tylko jedno rozwiązanie rzeczywiste 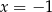 .
.

