Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 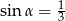 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
/Szkoła średnia
Pierwiastkami trójmianu kwadratowego 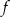 o współczynniku
o współczynniku 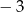 przy najwyższej potędze są liczby
przy najwyższej potędze są liczby 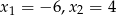 . Oblicz
. Oblicz 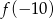 .
.
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 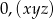 . Wiemy, że cyfra znajdująca się na 22 miejscu po przecinku tego rozwinięcia jest równa 7, cyfra znajdująca się na miejscu 26 jest równa 3, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 22 miejscu po przecinku tego rozwinięcia jest równa 7, cyfra znajdująca się na miejscu 26 jest równa 3, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka  jest więc równy
jest więc równy
A) 732 B) 273 C) 244 D) 723
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 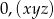 . Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka  jest więc równy
jest więc równy
A) 79 B) 273 C) 237 D) 244
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 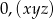 . Wiemy, że cyfra znajdująca się na 19 miejscu po przecinku tego rozwinięcia jest równa 3, cyfra znajdująca się na miejscu 26 jest równa 7, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 19 miejscu po przecinku tego rozwinięcia jest równa 3, cyfra znajdująca się na miejscu 26 jest równa 7, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka  jest więc równy
jest więc równy
A) 372 B) 273 C) 244 D) 124
Rozwiąż równanie 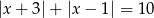 .
.
Rozwiąż równanie 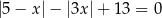 .
.
Rozwiąż równanie 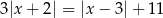 .
.
Rozwiąż równanie 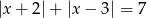 .
.
Rozwiąż równanie 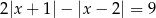 .
.
Rozwiąż równanie 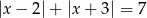 .
.
Dany jest trójkąt równoboczny 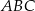 o boku długości 24. Punkt
o boku długości 24. Punkt 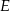 leży na boku
leży na boku 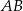 , a punkt
, a punkt 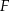 – na boku
– na boku 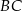 tego trójkąta. Odcinek
tego trójkąta. Odcinek 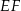 jest równoległy do boku
jest równoległy do boku 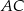 i przechodzi przez środek
i przechodzi przez środek 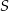 wysokości
wysokości 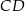 trójkąta
trójkąta 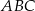 (zobacz rysunek).
(zobacz rysunek).
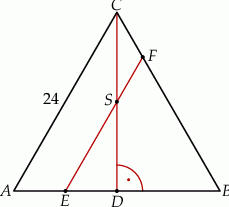
Oblicz długość odcinka 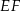 .
.
Wyznacz wszystkie wartości  , dla których liczby
, dla których liczby 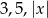 mogą być długościami boków trójkąta.
mogą być długościami boków trójkąta.
Trzy książki, których ceny tworzą ciąg geometryczny zakupiono płacąc łącznie 76 zł. Najdroższa z nich kosztowała o 4 zł mniej niż dwie pozostałe razem. Ile kosztowała każda książka?
Rozwiąż nierówność liniową 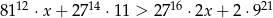 .
.
Suma trzech początkowych wyrazów rosnącego ciągu geometrycznego 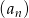 , określonego dla
, określonego dla 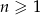 , jest równa
, jest równa 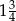 . Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego
. Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego 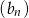 ,
, 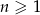 . Wyznacz wzór ciągu
. Wyznacz wzór ciągu 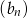 .
.
Przekątne trapezu 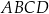 przecinają się w punkcie
przecinają się w punkcie  w ten sposób, że
w ten sposób, że 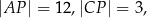
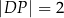 . Długość odcinka
. Długość odcinka 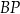 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Przekątne trapezu 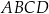 o podstawach
o podstawach 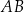 i
i 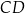 przecinają się w punkcie
przecinają się w punkcie 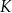 w ten sposób, że
w ten sposób, że 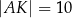 ,
, 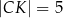 ,
, 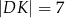 . Długość odcinka
. Długość odcinka 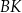 jest równa
jest równa
A) 7 B) 14 C) 10 D) 8
Przekątne trapezu 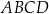 przecinają się w punkcie
przecinają się w punkcie 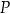 w ten sposób, że
w ten sposób, że 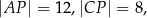
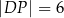 . Długość odcinka
. Długość odcinka 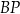 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Udowodnij, że dla dowolnych liczb dodatnich 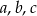 i
i 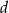 prawdziwa jest nierówność
prawdziwa jest nierówność
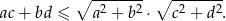
Dla jakich wartości parametru 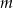 równanie
równanie 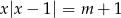 ma dwa różne rozwiązania?
ma dwa różne rozwiązania?
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej ma długość 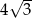 , a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 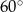 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Trójkąt równoboczny 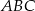 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 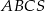 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 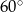 , a krawędź boczna ma długość
, a krawędź boczna ma długość 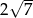 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
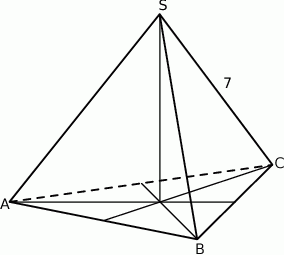
Trójkąt równoboczny 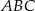 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 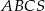 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 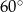 , a krawędź boczna ma długość 7 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
, a krawędź boczna ma długość 7 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
Podaj dla jakich wartości parametru 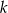 punkt przecięcia się wykresów funkcji
punkt przecięcia się wykresów funkcji 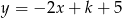 i
i 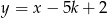 należy do koła o środku
należy do koła o środku 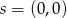 i promieniu
i promieniu 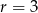 .
.
W ciągu arytmetycznym 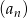 dla
dla 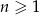 ,
, 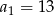 oraz
oraz 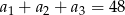 . Wtedy suma
. Wtedy suma 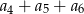 jest równa
jest równa
A) 48 B) 96 C) 75 D) 58
Dwaj równorzędni przeciwnicy grają w szachy. Co jest bardziej prawdopodobne:
- wygranie dwóch partii z trzech, czy czterech partii z sześciu rozegranych?
- wygranie nie mniej niż dwóch partii z trzech, czy nie mniej niż czterech partii z sześciu rozegranych? (Remisów nie uwzględniamy.)
Przekątna równoległoboku dzieli go na dwa trójkąty równoramienne (zobacz rysunek).
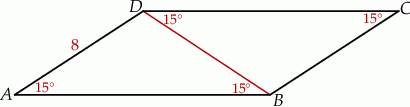
Pole tego równoległoboku jest równe
A) 16 B) 32 C) 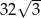 D)
D) 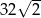
W trójkącie 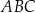 symetralna boku
symetralna boku 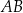 dzieli bok
dzieli bok 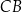 na odcinki długości
na odcinki długości 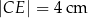 i
i 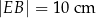 . Bok
. Bok 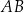 ma 16 cm długości. Wyznacz długości odcinków, na jakie wysokość
ma 16 cm długości. Wyznacz długości odcinków, na jakie wysokość 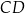 podzieliła bok
podzieliła bok 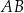 .
.
W kartezjańskim układzie współrzędnych 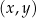 środek
środek 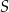 okręgu o promieniu
okręgu o promieniu 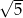 leży na prostej o równaniu
leży na prostej o równaniu 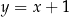 . Przez punkt
. Przez punkt 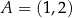 , którego odległość od punktu
, którego odległość od punktu 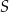 jest większa od
jest większa od 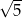 , poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio –
, poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio – 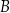 i
i 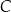 . Pole czworokąta
. Pole czworokąta 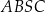 jest równe 15. Oblicz współrzędne punktu
jest równe 15. Oblicz współrzędne punktu 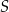 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.
W kartezjańskim układzie współrzędnych 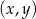 przedstawiono oś symetrii wykresu funkcji kwadratowej
przedstawiono oś symetrii wykresu funkcji kwadratowej 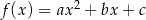 . Przedstawiono również prostą
. Przedstawiono również prostą 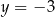 , z którą wykres funkcji
, z którą wykres funkcji 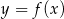 ma dokładnie jeden punkt wspólny, oraz jeden z punktów tego wykresu –
ma dokładnie jeden punkt wspólny, oraz jeden z punktów tego wykresu – 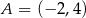
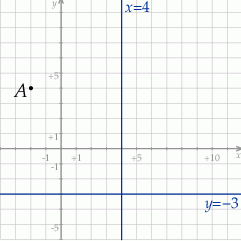
Wyznacz zbiór rozwiązań nierówności 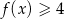 .
.

