Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 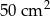 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
/Szkoła średnia
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 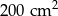 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 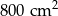 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
W klasie na początku roku było 30 uczniów. W ciągu roku z klasy odeszło 20% dziewcząt i przybyło 60% chłopców. Na koniec roku liczba dziewcząt i chłopców w klasie była równa. Ile dziewcząt, i ilu chłopców liczyła klasa na początku roku?
W pierwszym etapie konkursu matematycznego startowało 100 uczniów. Po pierwszym etapie z konkursu odpadło 50% dziewczynek oraz 15 chłopców. W drugim etapie konkursu wzięło udział trzy razy więcej chłopców niż dziewcząt. Ilu chłopców i ile dziewcząt wzięło udział w drugim etapie konkursu?
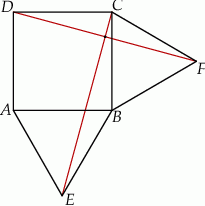
Na zewnątrz kwadratu 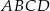 na bokach
na bokach 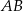 i
i 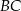 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 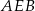 i
i 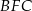 . Uzasadnij, że proste
. Uzasadnij, że proste 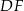 i
i 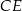 są prostopadłe.
są prostopadłe.
Dziedziną wyrażenia wymiernego 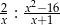 jest zbiór
jest zbiór
A) 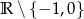 B)
B) 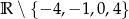 C)
C) 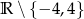 D)
D) 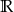
Dziedziną wyrażenia wymiernego 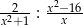 jest zbiór
jest zbiór
A) 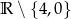 B)
B) 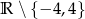 C)
C) 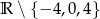 D)
D) 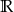
Dziedziną wyrażenia wymiernego 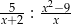 jest zbiór
jest zbiór
A) 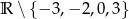 B)
B) 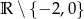 C)
C) 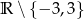 D)
D) 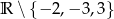
Dane jest równanie 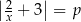 z niewiadomą
z niewiadomą  . Wyznacz liczbę rozwiązań tego równania w zależności od parametru
. Wyznacz liczbę rozwiązań tego równania w zależności od parametru 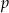 .
.
Wyznacz te wartości parametru 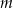 , dla których równanie
, dla których równanie 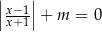 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Oblicz objętość tego graniastosłupa jeżeli jego pole powierzchni całkowitej jest równe 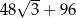 .
.
Rosnące, trzywyrazowe ciągi arytmetyczny i geometryczny mają pierwsze wyrazy równe 9. Trzecie wyrazy tych ciągów są także równe. Drugi wyraz ciągu arytmetycznego jest o 2 większy od drugiego wyrazu ciągu geometrycznego. Wyznacz te ciągi.
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.
W trójkącie 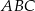 , w którym
, w którym 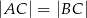 , na boku
, na boku 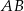 wybrano punkt
wybrano punkt 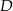 taki, że
taki, że 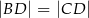 oraz
oraz 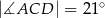 (zobacz rysunek).
(zobacz rysunek).
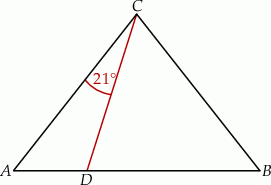
Wynika stąd, że kąt 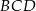 ma miarę
ma miarę
A) 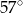 B)
B) 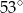 C)
C) 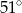 D)
D) 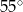
Dany jest trójkąt równoramienny 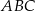 , w którym
, w którym 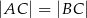 . Na podstawie
. Na podstawie 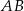 tego trójkąta leży punkt
tego trójkąta leży punkt 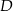 , taki że
, taki że 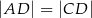 ,
, 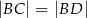 oraz
oraz 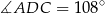 (zobacz rysunek).
(zobacz rysunek).
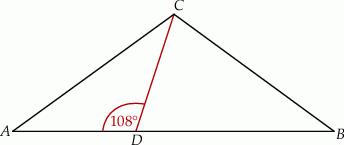
Wynika stąd, że kąt 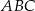 ma miarę
ma miarę
A) 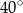 B)
B) 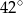 C)
C) 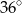 D)
D) 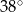
Dany jest trójkąt równoramienny 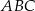 , w którym
, w którym 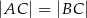 . Na podstawie
. Na podstawie 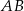 tego trójkąta leży punkt
tego trójkąta leży punkt 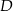 , taki że
, taki że 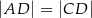 ,
, 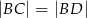 oraz
oraz 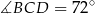 (zobacz rysunek).
(zobacz rysunek).
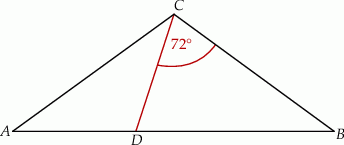
Wynika stąd, że kąt 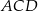 ma miarę
ma miarę
A) 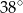 B)
B) 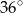 C)
C) 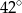 D)
D) 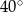
W trójkącie 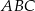 , w którym
, w którym 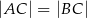 , na boku
, na boku 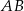 wybrano punkt
wybrano punkt 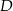 taki, że
taki, że 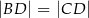 oraz
oraz 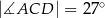 (zobacz rysunek).
(zobacz rysunek).
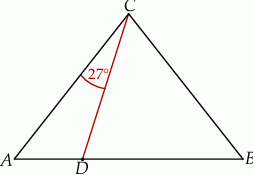
Wynika stąd, że kąt 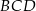 ma miarę
ma miarę
A) 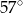 B)
B) 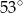 C)
C) 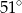 D)
D) 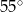
Ze zbioru liczb 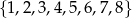 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 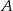 , polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.
, polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.
Ze zbioru dziewięcioelementowego 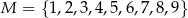 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 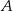 polega na wylosowaniu dwóch liczb ze zbioru
polega na wylosowaniu dwóch liczb ze zbioru 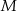 , których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia
, których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia 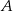 .
.
Ze zbioru ośmioelementowego 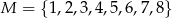 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 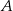 polega na wylosowaniu dwóch liczb ze zbioru
polega na wylosowaniu dwóch liczb ze zbioru 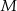 , których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia
, których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia 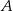 .
.
Ze zbioru liczb 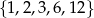 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 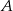 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą parzystą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą parzystą.
Ze zbioru liczb 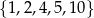 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 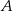 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 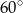 . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?
. Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?
Okrąg o środku 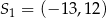 oraz okrąg o środku
oraz okrąg o środku 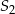 i promieniu 8 są styczne zewnętrznie w punkcie
i promieniu 8 są styczne zewnętrznie w punkcie 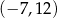 . Wtedy
. Wtedy
A) 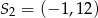 B)
B) 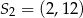 C)
C) 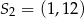 D)
D) 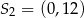
Zbiorem wartości funkcji kwadratowej 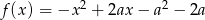 jest przedział
jest przedział 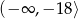 . Zatem
. Zatem
A) 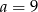 B)
B) 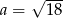 C)
C) 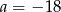 D)
D) 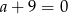
Reszta z dzielenia wielomianu 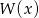 przez dwumian
przez dwumian 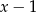 jest równa 1, zaś reszta z dzielenia tego wielomianu przez
jest równa 1, zaś reszta z dzielenia tego wielomianu przez 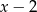 jest równa 4. Wyznacz resztę z dzielenia wielomianu
jest równa 4. Wyznacz resztę z dzielenia wielomianu 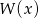 przez wielomian
przez wielomian 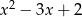 .
.
Wyznacz resztę z dzielenia wielomianu 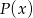 przez trójmian
przez trójmian 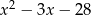 jeśli
jeśli 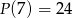 i
i 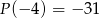 .
.
Poniżej przedstawiony jest wykres funkcji 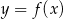 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
- dziedzinę funkcji
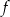 ,
, - zbiór wartości funkcji
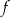 ,
, - maksymalne przedziały, w których funkcja
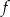 jest malejąca,
jest malejąca, - miejsca zerowe funkcji
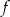 ,
, - zbiór argumentów, dla których funkcja
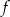 przyjmuje wartości nieujemne.
przyjmuje wartości nieujemne.
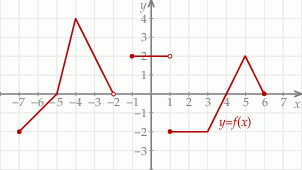
Poniżej przedstawiony jest wykres funkcji 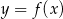 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
- wartość wyrażenia
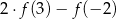 ,
, - dziedzinę funkcji
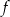 ,
, - maksymalne przedziały, w których funkcja
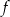 jest rosnąca,
jest rosnąca, - zbiór argumentów, dla których funkcja
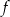 przyjmuje wartości niedodatnie.
przyjmuje wartości niedodatnie.
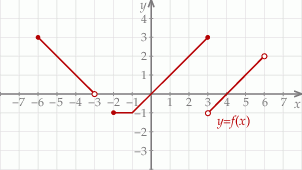
Poniżej przedstawiony jest wykres funkcji 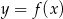 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
- dziedzinę funkcji
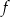 ,
, - zbiór wartości funkcji
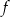 ,
, - maksymalne przedziały, w których funkcja
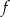 jest rosnąca,
jest rosnąca, - miejsca zerowe funkcji
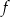 ,
, - zbiór argumentów, dla których funkcja
 przyjmuje wartości niedodatnie.
przyjmuje wartości niedodatnie.
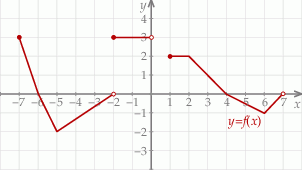
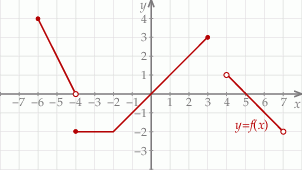
Poniżej przedstawiony jest wykres funkcji 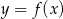 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
- wartość wyrażenia
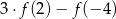 ,
, - dziedzinę funkcji
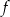 ,
, - maksymalne przedziały, w których funkcja
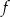 jest malejąca,
jest malejąca, - zbiór argumentów, dla których funkcja
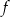 przyjmuje wartości nieujemne.
przyjmuje wartości nieujemne.
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 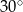 B)
B) 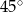 C)
C) 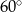 D)
D) 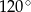
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od przekątnej podstawy tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 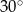 B)
B) 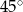 C)
C) 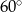 D)
D) 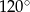
Długość przekątnej podstawy graniastosłupa prawidłowego czworokątnego jest równa długości jego wysokości. Z tego wynika, że miara kąta, jaki tworzy przekątna graniastosłupa z podstawą, jest równa
A) 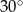 B)
B) 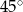 C)
C) 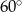 D)
D) 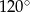
Pierwszy, trzeci i jedenasty wyraz ciągu arytmetycznego o różnicy 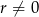 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 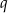 . Dla jakich wartości parametru
. Dla jakich wartości parametru 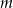 funkcja
funkcja 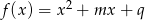 osiąga minimum większe od
osiąga minimum większe od 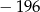 ?
?
Wyznacz wszystkie wartości parametrów 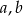 , dla których nierówność
, dla których nierówność
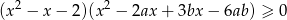
jest spełniona przez każdą liczbę rzeczywistą.
Wielomian 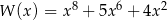 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 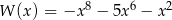 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 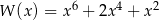 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) wartości niedodatnie B) wartości nieujemne
C) tylko wartości ujemne D) tylko wartości dodatnie
Wyznacz wszystkie wartości parametru 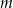 , dla których równanie
, dla których równanie 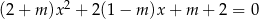 ma dwa różne pierwiastki rzeczywiste i kwadrat sumy odwrotności tych pierwiastków nie jest mniejszy od 0,5.
ma dwa różne pierwiastki rzeczywiste i kwadrat sumy odwrotności tych pierwiastków nie jest mniejszy od 0,5.

