W ciągu arytmetycznym 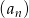 , określonym dla
, określonym dla 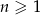 , dane są dwa wyrazy:
, dane są dwa wyrazy: 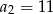 i
i 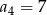 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 36 B) 40 C) 13 D) 20
/Szkoła średnia/Zadania testowe/Ciągi/Arytmetyczny/Dane dwa wyrazy
W ciągu arytmetycznym 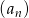 , określonym dla
, określonym dla 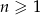 , dane są dwa wyrazy:
, dane są dwa wyrazy: 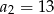 i
i 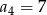 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 92 B) 39 C) 46 D) 50
W ciągu arytmetycznym 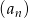 dane są
dane są 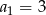 i
i 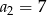 . Wtedy suma
. Wtedy suma 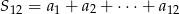 jest równa
jest równa
A) 324 B) 300 C) 282 D) 306
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 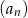 , w którym
, w którym 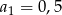 oraz
oraz 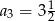 jest równa
jest równa
A) 295 B) 298 C) 305 D) 308
Wzór ogólny ciągu arytmetycznego, w którym 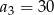 i
i 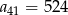 , to
, to
A) 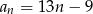 B)
B) 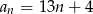 C)
C) 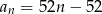 D)
D) 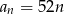
W ciągu arytmetycznym 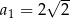 i
i 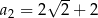 . Suma wyrazów od dziesiątego do czterdziestego włącznie jest równa
. Suma wyrazów od dziesiątego do czterdziestego włącznie jest równa
A) 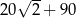 B)
B) 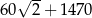 C)
C) 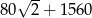 D)
D) 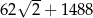
Dwa kolejne wyrazy ciągu arytmetycznego są równe 79 i 75. Wyrazem tego ciągu może być liczba
A) 2015 B) 2016 C) 2017 D) 2018
Pierwszy wyraz ciągu arytmetycznego jest równy 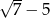 , a drugi wyraz jest równy
, a drugi wyraz jest równy 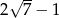 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 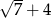 B)
B) 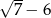 C)
C) 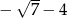 D)
D) 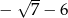
Pierwszy wyraz ciągu arytmetycznego jest równy 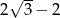 , a drugi wyraz jest równy
, a drugi wyraz jest równy 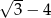 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 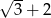 B)
B) 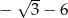 C)
C) 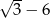 D)
D) 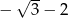
Pierwszy wyraz ciągu arytmetycznego jest równy 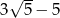 , a drugi wyraz jest równy
, a drugi wyraz jest równy 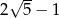 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 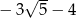 B)
B) 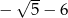 C)
C) 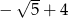 D)
D) 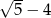
Pierwszy wyraz ciągu arytmetycznego jest równy 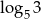 , a drugi wyraz
, a drugi wyraz 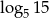 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 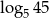 B)
B) 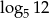 C) 1 D) 12
C) 1 D) 12
Pierwszy wyraz ciągu arytmetycznego jest równy 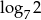 , a drugi wyraz
, a drugi wyraz 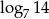 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 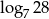 B) 1 C)
B) 1 C) 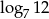 D) 7
D) 7
Pierwszy wyraz ciągu arytmetycznego jest równy 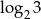 , a drugi wyraz
, a drugi wyraz 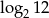 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 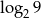 B) 2 C)
B) 2 C) 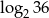 D) -2
D) -2
Dany jest ciąg arytmetyczny 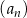 , określony dla
, określony dla 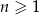 , o którym wiemy, że:
, o którym wiemy, że: 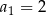 i
i 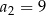 . Wtedy
. Wtedy 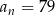 dla
dla
A) 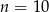 B)
B) 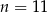 C)
C) 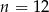 D)
D) 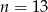
Dany jest ciąg arytmetyczny 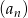 , określony dla
, określony dla 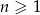 , o którym wiemy, że:
, o którym wiemy, że: 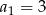 i
i 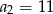 . Wtedy
. Wtedy 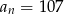 dla
dla
A) 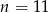 B)
B) 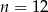 C)
C) 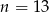 D)
D) 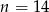
W ciągu arytmetycznym 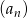 , określonym dla
, określonym dla 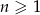 , dane są:
, dane są: 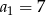 ,
, 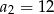 . Wtedy
. Wtedy
A) 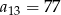 B)
B) 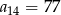 C)
C) 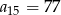 D)
D) 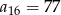
W ciągu arytmetycznym 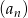 , określonym dla
, określonym dla 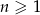 , dane są:
, dane są: 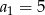 ,
, 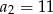 . Wtedy
. Wtedy
A) 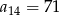 B)
B) 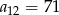 C)
C) 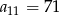 D)
D) 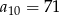
Liczby 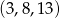 są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
A) 48 B) 103 C) 168 D) 190
Liczby 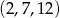 są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
A) 47 B) 112 C) 179 D) 147
Liczby 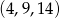 są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
A) 49 B) 191 C) 169 D) 104
W ciągu arytmetycznym 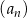 , określonym dla
, określonym dla 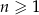 , dane są dwa wyrazy:
, dane są dwa wyrazy: 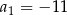 oraz
oraz 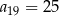 . Wtedy suma
. Wtedy suma
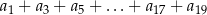
jest równa
A) 133 B) 63 C) 70 D) 49
Ciąg arytmetyczny 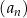 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 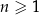 . W tym ciągu
. W tym ciągu 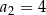 oraz
oraz 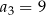 . Szósty wyraz ciągu
. Szósty wyraz ciągu 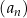 jest równy
jest równy
A) 24 B) 29 C) 36 D) 69
Ciąg arytmetyczny 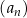 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 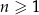 . W tym ciągu
. W tym ciągu 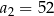 oraz
oraz 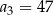 . Szósty wyraz ciągu
. Szósty wyraz ciągu 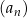 jest równy
jest równy
A) 32 B) 62 C) 37 D) 27
Ciąg arytmetyczny 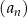 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 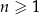 . W tym ciągu
. W tym ciągu 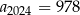 oraz
oraz 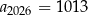 . Wyraz
. Wyraz 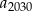 tego ciągu jest równy
tego ciągu jest równy
A) 1100,5 B) 1083 C) 1048 D) 1118
Ciąg 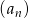 określony dla
określony dla 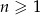 jest arytmetyczny oraz
jest arytmetyczny oraz 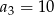 i
i 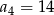 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 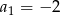 B)
B) 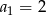 C)
C) 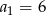 D)
D) 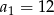
Ciąg 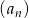 określony dla
określony dla 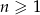 jest arytmetyczny oraz
jest arytmetyczny oraz 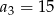 i
i 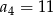 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 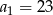 B)
B) 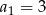 C)
C) 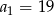 D)
D) 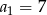
Liczby 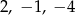 są trzema początkowymi wyrazami ciągu arytmetycznego
są trzema początkowymi wyrazami ciągu arytmetycznego 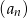 , określonego dla liczb naturalnych
, określonego dla liczb naturalnych 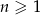 . Wzór ogólny tego ciągu ma postać
. Wzór ogólny tego ciągu ma postać
A) 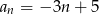 B)
B) 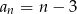 C)
C) 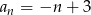 D)
D) 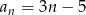
Liczby 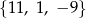 są trzema początkowymi wyrazami ciągu arytmetycznego
są trzema początkowymi wyrazami ciągu arytmetycznego 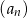 , określonego dla liczb naturalnych
, określonego dla liczb naturalnych 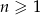 . Wzór ogólny tego ciągu ma postać
. Wzór ogólny tego ciągu ma postać
A) 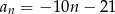 B)
B) 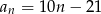 C)
C) 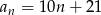 D)
D) 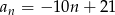
W ciągu arytmetycznym 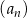 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 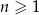 , są dane dwa wyrazy:
, są dane dwa wyrazy: 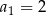 i
i 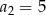 . Stąd wynika, że
. Stąd wynika, że  –ty wyraz tego ciągu jest określony wzorem
–ty wyraz tego ciągu jest określony wzorem
A) 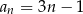 B)
B) 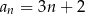 C)
C) 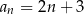 D)
D) 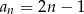
W ciągu arytmetycznym 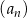 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 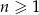 , są dane dwa wyrazy:
, są dane dwa wyrazy: 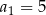 i
i 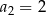 . Stąd wynika, że
. Stąd wynika, że  –ty wyraz tego ciągu jest określony wzorem
–ty wyraz tego ciągu jest określony wzorem
A) 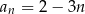 B)
B) 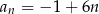 C)
C) 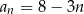 D)
D) 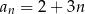
Liczby 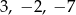 są trzema początkowymi wyrazami ciągu arytmetycznego
są trzema początkowymi wyrazami ciągu arytmetycznego 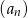 , określonego dla liczb naturalnych
, określonego dla liczb naturalnych 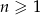 . Wzór ogólny tego ciągu ma postać
. Wzór ogólny tego ciągu ma postać
A) 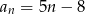 B)
B) 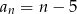 C)
C) 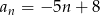 D)
D) 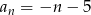
W ciągu arytmetycznym trzeci wyraz jest równy 14, a jedenasty jest równy 34. Różnica tego ciągu jest równa
A) 9 B)  C) 2 D)
C) 2 D) 
W ciągu arytmetycznym piąty wyraz jest równy 11, a dziewiąty jest równy 25. Różnica tego ciągu jest równa
A) 14 B) 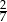 C) 7 D)
C) 7 D) 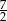
Trzydziesty wyraz ciągu arytmetycznego 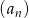 jest równy 4, a trzydziesty piąty wyraz tego ciągu jest równy 7. Wówczas różnica ciągu
jest równy 4, a trzydziesty piąty wyraz tego ciągu jest równy 7. Wówczas różnica ciągu 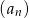 jest równa
jest równa
A) 5 B) 3 C) 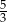 D)
D) 
Dany jest ciąg arytmetyczny 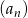 dla
dla 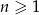 , w którym
, w którym 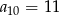 oraz
oraz 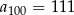 . Wtedy różnica
. Wtedy różnica  tego ciągu jest równa
tego ciągu jest równa
A) 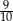 B)
B) 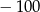 C)
C) 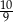 D) 100
D) 100
W ciągu arytmetycznym czwarty wyraz jest równy 13, a jedenasty jest równy 34. Różnica tego ciągu jest równa
A) 3 B) 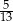 C) 21 D)
C) 21 D) 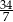
W ciągu arytmetycznym 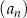 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 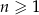 ,
, 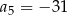 oraz
oraz 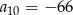 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 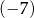 B)
B) 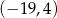 C) 7 D) 19,4
C) 7 D) 19,4
W ciągu arytmetycznym trzeci wyraz jest równy 12, a jedenasty jest równy 42. Różnica tego ciągu jest równa
A) 30 B) 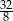 C) 8 D)
C) 8 D) 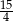
Dany jest ciąg arytmetyczny 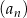 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 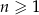 . W tym ciągu
. W tym ciągu 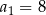 ,
, 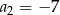 ,
, 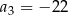 .
.
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór ogólny ciągu 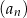 ma postać
ma postać
A) 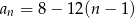 B)
B) 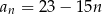
C) 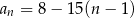 D)
D) 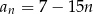
E) 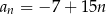 F)
F) 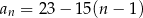
Drugi wyraz ciągu arytmetycznego jest równy 12, a trzeci wyraz jest równy 5. Wzór na ogólny wyraz tego ciągu to
A) 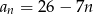 B)
B) 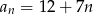 C)
C) 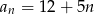 D)
D) 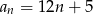
Drugi wyraz ciągu arytmetycznego jest równy 5, a trzeci wyraz jest równy 12. Wzór na ogólny wyraz tego ciągu to
A) 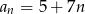 B)
B) 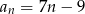 C)
C) 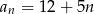 D)
D) 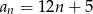
Drugi wyraz ciągu arytmetycznego jest równy 10, a trzeci wyraz jest równy 6. Wzór na ogólny wyraz tego ciągu to
A) 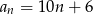 B)
B) 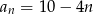 C)
C) 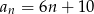 D)
D) 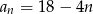
Dwa wyrazy ciągu arytmetycznego o wyrazach całkowitych są równe 200 i 101. Różnica tego ciągu może być równa
A) 5 B) 18 C) 11 D) 199
Dwa wyrazy ciągu arytmetycznego o wyrazach całkowitych są równe 319 i 409. Różnica tego ciągu może być równa
A) 12 B) 18 C) 11 D) 19
W ciągu arytmetycznym 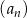 , określonym dla
, określonym dla 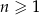 , wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15. Jednym z wyrazów tego ciągu jest liczba
, wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15. Jednym z wyrazów tego ciągu jest liczba
A) 2023 B) 1945 C) 1410 D) 2000
Dany jest ciąg arytmetyczny 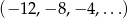 . Czterdziesty wyraz tego ciągu jest równy
. Czterdziesty wyraz tego ciągu jest równy
A) -148 B) 144 C) 148 D) 166
W ciągu arytmetycznym 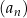 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 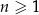 , dane są wyrazy:
, dane są wyrazy: 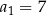 oraz
oraz 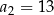 . Wyraz
. Wyraz 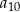 jest równy
jest równy
A) 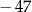 B) 52 C) 61 D) 67
B) 52 C) 61 D) 67
Dany jest ciąg arytmetyczny 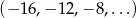 . Trzydziesty wyraz tego ciągu jest równy
. Trzydziesty wyraz tego ciągu jest równy
A) -132 B) -136 C) 100 D) 104
Osiemnasty wyraz ciągu arytmetycznego 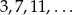 jest równy:
jest równy:
A) 71 B) 68 C) 75 D) 72
Dany jest ciąg arytmetyczny 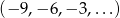 . Czterdziesty wyraz tego ciągu jest równy
. Czterdziesty wyraz tego ciągu jest równy
A) -111 B) 126 C) 111 D) 108
Suma wszystkich wyrazów ciągu arytmetycznego, w którym 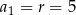 , a ostatni wyraz wynosi 250 jest równa
, a ostatni wyraz wynosi 250 jest równa
A) 6385 B) 6475 C) 6375 D) 6575

