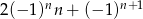Dany jest ciąg 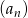 , w którym
, w którym 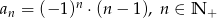 . Jeśli
. Jeśli 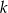 jest liczbą naturalną nieparzystą, to:
jest liczbą naturalną nieparzystą, to:
A) 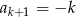 B)
B) 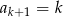 C)
C) 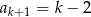 D)
D) 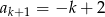
/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Różne
Dany jest ciąg 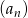 , w którym
, w którym 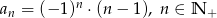 . Jeśli
. Jeśli 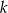 jest liczbą naturalną parzystą, to:
jest liczbą naturalną parzystą, to:
A) 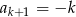 B)
B) 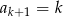 C)
C) 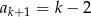 D)
D) 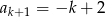
W ciągu 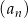 określonym dla każdej liczby
określonym dla każdej liczby 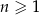 jest spełniony warunek
jest spełniony warunek 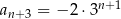 . Wtedy
. Wtedy
A) 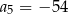 B)
B) 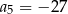 C)
C) 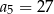 D)
D) 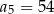
W ciągu 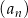 określonym dla każdej liczby
określonym dla każdej liczby 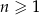 jest spełniony warunek
jest spełniony warunek 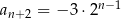 . Wtedy
. Wtedy
A) 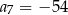 B)
B) 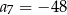 C)
C) 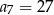 D)
D) 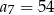
Liczba 5 jest czwartym wyrazem ciągu:
A) 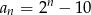 B)
B) 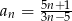 C)
C) 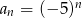 D)
D) 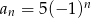
Dane są ciągi 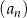 ,
, 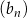 ,
, 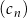 ,
, 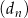 , określone dla każdej liczby naturalnej
, określone dla każdej liczby naturalnej 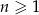 wzorami:
wzorami: 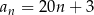 ,
, 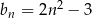 ,
, 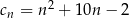 ,
, 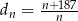 . Liczba 197 jest dziesiątym wyrazem ciągu
. Liczba 197 jest dziesiątym wyrazem ciągu
A) 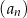 B)
B) 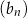 C)
C) 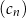 D)
D) 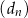
Dane są ciągi 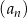 ,
, 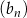 ,
, 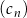 ,
, 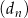 , określone dla każdej liczby naturalnej
, określone dla każdej liczby naturalnej 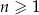 wzorami:
wzorami: 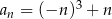 ,
, 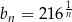 ,
, 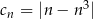 ,
, 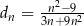 . Dodatnia liczba całkowita dwucyfrowa jest trzecim wyrazem ciągu
. Dodatnia liczba całkowita dwucyfrowa jest trzecim wyrazem ciągu
A) 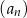 B)
B) 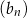 C)
C) 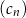 D)
D) 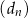
Dane są ciągi 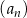 ,
, 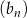 ,
, 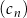 ,
, 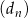 , określone dla każdej liczby naturalnej
, określone dla każdej liczby naturalnej 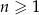 wzorami:
wzorami: 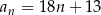 ,
, 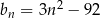 ,
, 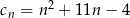 ,
, 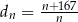 . Liczba 206 jest dziesiątym wyrazem ciągu
. Liczba 206 jest dziesiątym wyrazem ciągu
A) 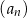 B)
B) 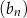 C)
C) 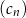 D)
D) 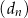
Setny wyraz ciągu 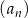 jest równy 2018. Wzór ogólny na
jest równy 2018. Wzór ogólny na  -ty wyraz ciągu
-ty wyraz ciągu 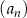 może mieć postać
może mieć postać
A) 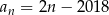 B)
B) 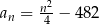 C)
C) 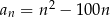 D)
D) 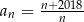
Setny wyraz ciągu 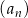 jest równy 2020. Wzór ogólny na
jest równy 2020. Wzór ogólny na  –ty wyraz ciągu
–ty wyraz ciągu 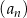 może mieć postać
może mieć postać
A) 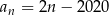 B)
B) 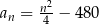 C)
C) 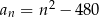 D)
D) 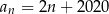
Dany jest ciąg 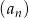 o wyrazie ogólnym
o wyrazie ogólnym 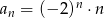 , dla
, dla 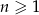 . Różnica wyrazów czwartego i piątego tego ciągu jest równa
. Różnica wyrazów czwartego i piątego tego ciągu jest równa
A) 96 B) 224 C) -96 D) -224
Dany jest ciąg 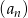 o wyrazie ogólnym
o wyrazie ogólnym 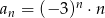 , gdzie
, gdzie 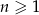 . Różnica wyrazów trzeciego i czwartego tego ciągu jest równa
. Różnica wyrazów trzeciego i czwartego tego ciągu jest równa
A) 1539 B) -1539 C) -96 D) -405
Dany jest ciąg 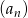 o wyrazie ogólnym
o wyrazie ogólnym 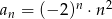 , gdzie
, gdzie 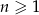 . Różnica wyrazu trzeciego i czwartego tego ciągu jest równa
. Różnica wyrazu trzeciego i czwartego tego ciągu jest równa
A) -328 B) 184 C) -184 D) 328
Liczby 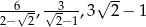 są kolejnymi wyrazami ciągu
są kolejnymi wyrazami ciągu
A) arytmetycznego B) geometrycznego C) rosnącego D) malejącego
Liczby 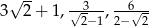 są kolejnymi wyrazami ciągu
są kolejnymi wyrazami ciągu
A) arytmetycznego B) geometrycznego C) rosnącego D) malejącego
Nieskończony ciąg liczbowy 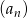 , w którym
, w którym
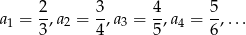
może być opisany wzorem:
A) 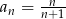 B)
B) 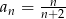 C)
C) 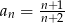 D)
D) 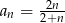
Wyraz ogólny ciągu 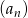 jest równy
jest równy 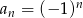 . Zatem
. Zatem 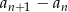 równa się
równa się
A) 0 B) 1 C) 2 lub -2 D) -2 lub 0
Wyraz ogólny ciągu 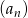 jest równy
jest równy 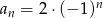 . Zatem
. Zatem 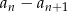 równa się
równa się
A) 0 B) 1 C) 2 lub -2 D) -4 lub 4
Wyraz ogólny ciągu 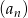 jest równy
jest równy 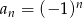 . Zatem
. Zatem 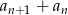 równa się
równa się
A) 0 B) 1 C) 2 lub -2 D) -1 lub 1
Ciąg 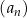 jest określony wzorem
jest określony wzorem
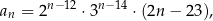
dla każdej liczby naturalnej 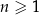 . Który wyraz ciągu
. Który wyraz ciągu 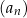 jest równy 466 560?
jest równy 466 560?
A) 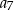 B)
B) 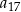 C)
C) 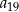 D)
D) 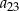
Ciąg 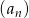 spełnia warunek
spełnia warunek 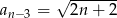 dla
dla 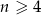 . Wówczas
. Wówczas
A) 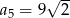 B)
B) 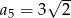 C)
C) 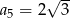 D)
D) 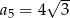
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 5 dają resztę 3. Dziesiąty wyraz tego ciągu jest równy
A) 43 B) 53 C) 58 D) 68
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 7 dają resztę 4. Dziewiąty wyraz tego ciągu jest równy
A) 53 B) 74 C) 60 D) 67
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 4 dają resztę 3. Dwunasty wyraz tego ciągu jest równy
A) 51 B) 55 C) 59 D) 63
Ciąg 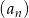 jest określony wzorem
jest określony wzorem 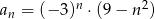 dla
dla 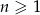 . Wynika stąd, że
. Wynika stąd, że
A) 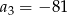 B)
B) 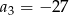 C)
C) 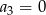 D)
D) 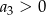
Ciąg 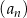 jest określony wzorem
jest określony wzorem 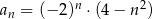 , dla
, dla 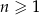 . Wtedy
. Wtedy
A) 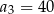 B)
B) 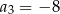 C)
C) 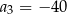 D)
D) 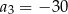
Ciąg 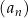 jest określony wzorem
jest określony wzorem 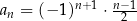 dla każdej liczby naturalnej
dla każdej liczby naturalnej 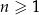 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 2 B) 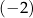 C) 3 D)
C) 3 D) 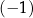
Ciąg 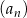 jest określony wzorem
jest określony wzorem 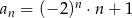 dla każdej liczby naturalnej
dla każdej liczby naturalnej 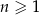 . Wtedy trzeci wyraz tego ciągu jest równy
. Wtedy trzeci wyraz tego ciągu jest równy
A) 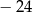 B)
B) 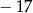 C)
C) 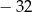 D)
D) 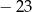
Ciąg 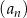 jest określony wzorem
jest określony wzorem 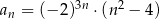 dla
dla 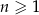 . Wówczas
. Wówczas
A) 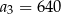 B)
B) 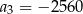 C)
C) 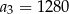 D)
D) 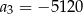
Ciąg 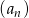 jest określony wzorem
jest określony wzorem 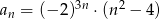 dla
dla 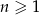 . Wówczas
. Wówczas
A) 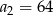 B)
B) 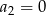 C)
C) 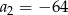 D)
D) 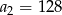
Dla 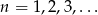 ciąg
ciąg 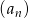 jest określony wzorem
jest określony wzorem 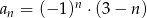 . Wtedy
. Wtedy
A) 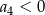 B)
B) 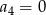 C)
C) 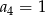 D)
D) 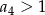
Ciąg 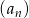 jest określony wzorem
jest określony wzorem 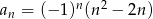 dla
dla 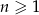 . Wtedy
. Wtedy
A) 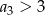 B)
B) 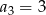 C)
C) 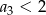 D)
D) 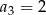
Dla 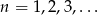 ciąg
ciąg 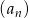 jest określony wzorem
jest określony wzorem 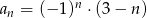 . Wtedy
. Wtedy
A) 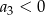 B)
B) 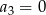 C)
C) 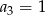 D)
D) 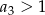
Ciąg 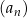 jest określony wzorem
jest określony wzorem 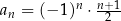 dla każdej liczby naturalnej
dla każdej liczby naturalnej 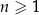 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 2 B) 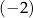 C) 3 D)
C) 3 D) 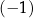
Trzywyrazowy ciąg 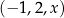 jest arytmetyczny. Trzywyrazowy ciąg
jest arytmetyczny. Trzywyrazowy ciąg 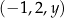 jest geometryczny. Liczby
jest geometryczny. Liczby  oraz
oraz 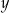 spełniają warunki
spełniają warunki
A) 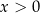 i
i 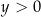 B)
B) 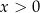 i
i 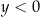 C)
C) 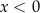 i
i 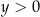 D)
D) 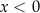 i
i 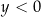
Ósmy wyraz ciągu 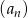 o wyrazie ogólnym
o wyrazie ogólnym 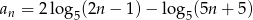 , gdzie
, gdzie 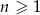 jest równy
jest równy
A) 1 B) 5 C) -1 D) -5
Siódmy wyraz ciągu 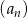 o wyrazie ogólnym
o wyrazie ogólnym 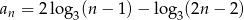 , gdzie
, gdzie 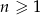 jest równy
jest równy
A) 1 B) 2 C) -1 D) -2
Ciąg 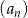 określony jest wzorem
określony jest wzorem 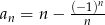 , gdzie
, gdzie 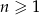 . Suma trzech początkowych wyrazów tego ciągu jest równa
. Suma trzech początkowych wyrazów tego ciągu jest równa
A) 7 B) 6 C) 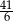 D)
D) 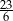
Ciąg 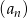 określony jest wzorem
określony jest wzorem 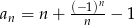 , gdzie
, gdzie 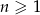 . Suma trzech początkowych wyrazów tego ciągu jest równa
. Suma trzech początkowych wyrazów tego ciągu jest równa
A) 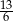 B) 6 C)
B) 6 C) 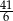 D)
D) 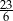
Ciąg 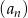 określony jest wzorem
określony jest wzorem 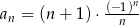 , gdzie
, gdzie 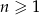 . Suma trzech początkowych wyrazów tego ciągu jest równa
. Suma trzech początkowych wyrazów tego ciągu jest równa
A) 3 B)  C)
C)  D)
D) 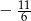
Ciąg 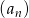 określony jest wzorem
określony jest wzorem 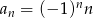 , gdzie
, gdzie 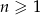 . Wówczas wyrażenie
. Wówczas wyrażenie 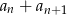 jest równe
jest równe
A) 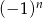 B)
B) 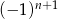 C)
C) 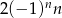 D)
D)