Dany jest ciąg 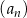 określony wzorem
określony wzorem 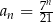 dla każdej liczby naturalnej
dla każdej liczby naturalnej 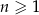 . Pięćdziesiątym wyrazem ciągu
. Pięćdziesiątym wyrazem ciągu 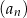 jest
jest
A) 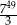 B)
B) 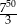 C)
C) 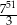 D)
D) 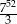
/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Różne
Ciąg 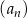 jest określony wzorem
jest określony wzorem 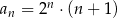 dla każdej liczby naturalnej
dla każdej liczby naturalnej 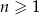 . Wyraz
. Wyraz 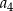 jest równy
jest równy
A) 64 B) 40 C) 48 D) 80
Ciąg 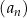 jest określony wzorem
jest określony wzorem 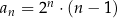 dla każdej liczby naturalnej
dla każdej liczby naturalnej 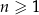 . Wyraz
. Wyraz 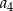 jest równy
jest równy
A) 64 B) 40 C) 48 D) 80
Ciąg 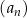 jest określony wzorem
jest określony wzorem 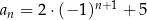 dla każdej liczby naturalnej
dla każdej liczby naturalnej 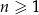 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 3 B) 7 C) 50 D) 100
Liczby 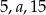 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 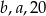 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 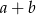 jest równa
jest równa
A) 20 B) 25 C) 15 D) 10
Liczby 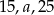 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 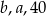 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 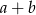 jest równa
jest równa
A) 40 B) 50 C) 20 D) 30
Liczby 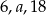 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 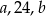 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 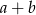 jest równa
jest równa
A) 60 B) 48 C) 12 D) 36
Jeżeli ciąg 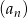 dany jest wzorem
dany jest wzorem 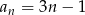 dla
dla 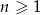 , to suma 10 początkowych wyrazów ciągu
, to suma 10 początkowych wyrazów ciągu 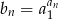 wyraża się wzorem
wyraża się wzorem
A) 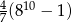 B)
B) 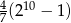 C)
C) 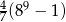 D)
D) 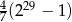
Ciąg 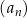 jest określony wzorem
jest określony wzorem 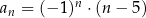 dla każdej liczby naturalnej
dla każdej liczby naturalnej 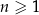 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwszy wyraz ciągu 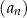 jest dwa razy większy od trzeciego wyrazu tego ciągu. jest dwa razy większy od trzeciego wyrazu tego ciągu. | P | F |
Wszystkie wyrazy ciągu 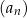 są dodatnie. są dodatnie. | P | F |
Ciąg 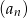 jest określony wzorem
jest określony wzorem 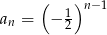 dla
dla 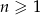 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 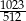 B)
B) 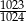 C)
C) 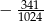 D)
D) 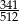
Wzór ogólny ciągu 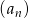 ma postać
ma postać 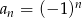 , dla
, dla 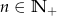 . Zatem ciąg ten jest
. Zatem ciąg ten jest
A) arytmetyczny B) geometryczny C) malejący D) rosnący
Ciąg 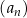 , określony wzorem
, określony wzorem 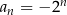 dla każdej liczby naturalnej
dla każdej liczby naturalnej 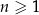 , jest
, jest
A) ciągiem arytmetycznym o różnicy 2.
B) ciągiem arytmetycznym o różnicy 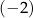 .
.
C) ciągiem geometrycznym o ilorazie 2.
D) ciągiem geometrycznym o ilorazie 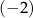 .
.
Wzór ogólny ciągu 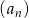 ma postać
ma postać 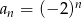 , dla
, dla 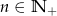 . Zatem ciąg ten jest
. Zatem ciąg ten jest
A) arytmetyczny B) malejący C) geometryczny D) rosnący
Ciąg 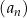 jest określony wzorem
jest określony wzorem 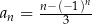 dla każdej liczby naturalnej
dla każdej liczby naturalnej 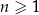 . Liczba wyrazów tego ciągu mniejszych od 12 jest równa
. Liczba wyrazów tego ciągu mniejszych od 12 jest równa
A) 36 B) 34 C) 33 D) 35
Ciągiem rosnącym jest ciąg o wyrazie ogólnym
A) 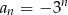 B)
B) 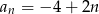 C)
C) 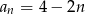 D)
D) 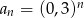
Ciągiem rosnącym jest ciąg o wyrazie ogólnym
A) 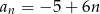 B)
B) 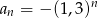 C)
C) 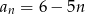 D)
D) 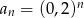
Ciągiem rosnącym jest ciąg o wyrazie ogólnym
A) 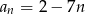 B)
B) 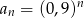 C)
C) 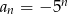 D)
D) 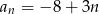
Dany jest ciąg 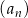 określony wzorem ogólnym
określony wzorem ogólnym 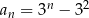 . Wyraz
. Wyraz 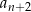 tego ciągu dla
tego ciągu dla 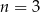 jest równy
jest równy
A) 3 B) 18 C) 27 D) 234
Ciąg liczbowy określony jest wzorem 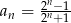 , dla
, dla 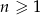 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 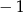 B)
B) 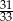 C)
C) 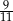 D) 1
D) 1
Ciąg liczbowy określony jest wzorem 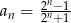 , dla
, dla 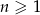 . Szósty wyraz tego ciągu jest równy
. Szósty wyraz tego ciągu jest równy
A) 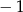 B)
B) 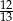 C)
C) 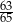 D) 1
D) 1
Liczba ujemnych wyrazów ciągu 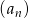 określonego wzorem
określonego wzorem 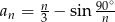 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Suma  początkowych liczb naturalnych dodatnich nieparzystych jest równa
początkowych liczb naturalnych dodatnich nieparzystych jest równa
A) 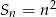 B)
B) 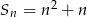 C)
C) 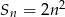 D)
D) 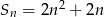
Suma  początkowych liczb naturalnych dodatnich parzystych jest równa
początkowych liczb naturalnych dodatnich parzystych jest równa
A) 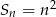 B)
B) 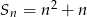 C)
C) 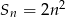 D)
D) 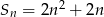
Suma  początkowych liczb naturalnych dodatnich podzielnych przez 3 jest równa
początkowych liczb naturalnych dodatnich podzielnych przez 3 jest równa
A) 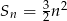 B)
B) 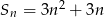 C)
C) 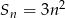 D)
D) 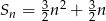
Dany jest ciąg o wzorze ogólnym 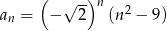 , gdzie
, gdzie 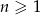 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 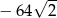 B)
B) 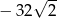 C)
C) 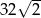 D)
D) 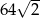
Ciąg 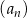 jest określony wzorem ogólnym
jest określony wzorem ogólnym 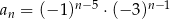 . Piąty wyraz tego ciągu ma wartość
. Piąty wyraz tego ciągu ma wartość
A) 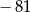 B) 81 C) 0 D) 243
B) 81 C) 0 D) 243
Dany jest ciąg 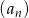 określony wzorem
określony wzorem 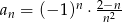 dla
dla 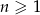 . Wówczas wyraz
. Wówczas wyraz 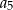 tego ciągu jest równy
tego ciągu jest równy
A) 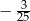 B)
B) 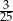 C)
C) 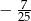 D)
D) 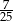
Dany jest ciąg o wzorze ogólnym 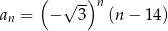 , gdzie
, gdzie 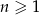 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 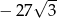 B)
B) 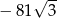 C)
C) 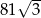 D)
D) 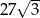
Ciąg 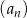 jest określony wzorem
jest określony wzorem 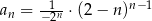 . Zatem
. Zatem
A) 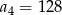 B)
B) 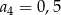 C)
C) 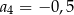 D)
D) 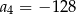
Ciąg 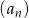 jest określony wzorem
jest określony wzorem 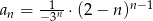 . Zatem
. Zatem
A) 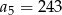 B)
B) 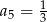 C)
C) 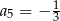 D)
D) 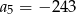
Ciąg 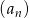 jest określony wzorem
jest określony wzorem 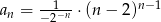 . Zatem
. Zatem
A) 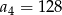 B)
B) 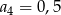 C)
C) 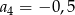 D)
D) 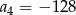
Ciąg 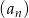 określony jest wzorem
określony jest wzorem 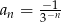 . Czwarty wyraz tego ciągu to
. Czwarty wyraz tego ciągu to
A) 81 B) 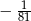 C) -81 D)
C) -81 D) 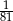
Czwarty wyraz ciągu 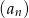 danego wzorem
danego wzorem 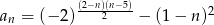 jest równy
jest równy
A) 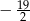 B)
B) 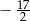 C) -11 D) 7
C) -11 D) 7
Dany jest ciąg 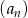 określony wzorem
określony wzorem 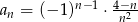 dla
dla 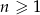 . Wówczas wyraz
. Wówczas wyraz 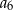 tego ciągu jest równy
tego ciągu jest równy
A) 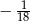 B)
B) 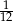 C)
C) 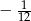 D)
D) 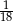
Ciąg 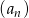 jest określony wzorem ogólnym
jest określony wzorem ogólnym 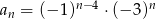 . Piąty wyraz tego ciągu ma wartość
. Piąty wyraz tego ciągu ma wartość
A) 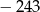 B) 243 C) 0 D)
B) 243 C) 0 D) 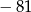
Dany jest ciąg 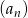 określony wzorem
określony wzorem 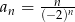 dla
dla 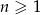 . Wówczas
. Wówczas
A) 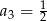 B)
B) 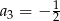 C)
C) 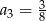 D)
D) 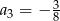
Ciąg 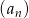 określony jest wzorem
określony jest wzorem 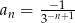 . Piąty wyraz tego ciągu to
. Piąty wyraz tego ciągu to
A) 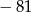 B)
B) 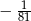 C) 81 D)
C) 81 D) 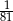
Ciąg 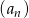 jest określony wzorem ogólnym
jest określony wzorem ogólnym 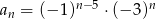 . Piąty wyraz tego ciągu ma wartość
. Piąty wyraz tego ciągu ma wartość
A) 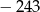 B) 243 C) 0 D)
B) 243 C) 0 D) 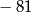
Drugi wyraz ciągu 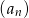 danego wzorem
danego wzorem 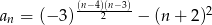 jest równy
jest równy
A) 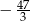 B)
B) 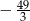 C) -13 D) -19
C) -13 D) -19
Dany jest ciąg o wzorze ogólnym 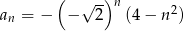 , gdzie
, gdzie 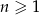 . Szósty wyraz tego ciągu jest równy
. Szósty wyraz tego ciągu jest równy
A) -256 B) 256 C) 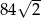 D)
D) 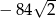
Ciąg 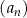 jest określony wzorem
jest określony wzorem 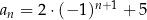 dla każdej liczby naturalnej
dla każdej liczby naturalnej 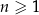 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ciąg 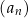 jest malejący. jest malejący. | P | F |
Ciąg 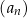 jest geometryczny. jest geometryczny. | P | F |
Ciąg 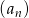 jest określony wzorem
jest określony wzorem 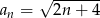 dla
dla 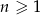 . Wówczas
. Wówczas
A) 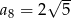 B)
B) 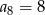 C)
C) 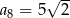 D)
D) 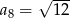
Ciąg 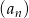 jest określony wzorem
jest określony wzorem 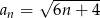 dla
dla 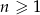 . Wówczas
. Wówczas
A) 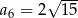 B)
B) 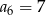 C)
C) 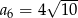 D)
D) 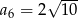
Ciąg 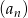 dany jest wzorem,
dany jest wzorem, 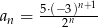 . Ciąg
. Ciąg 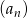 jest ciągiem
jest ciągiem
A) rosnącym B) malejącym C) arytmetycznym D) geometrycznym
Ciąg 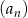 dany jest wzorem,
dany jest wzorem, 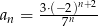 . Ciąg
. Ciąg 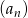 jest ciągiem
jest ciągiem
A) rosnącym B) malejącym C) geometrycznym D) arytmetycznym
Wyrazami ciągu 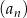 danego wzorem
danego wzorem 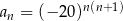
A) są zawsze liczby mniejsze od 1 B) są zawsze liczby dodatnie
C) są zawsze liczby ujemne D) są zarówno liczby dodatnie, jak i ujemne
Wyrazami ciągu 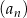 danego wzorem
danego wzorem 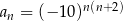
A) są zawsze liczby mniejsze od 1 B) są zawsze liczby dodatnie
C) są zawsze liczby ujemne D) są zarówno liczby dodatnie, jak i ujemne
Ciąg 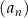 jest określony wzorem
jest określony wzorem 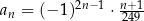 dla każdej liczby naturalnej
dla każdej liczby naturalnej 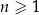 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wśród wyrazów ciągu 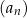 są zarówno liczby dodatnie jak i liczby ujemne. są zarówno liczby dodatnie jak i liczby ujemne. | P | F |
Wśród wyrazów ciągu 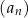 jest co najmniej 10 liczb całkowitych. jest co najmniej 10 liczb całkowitych. | P | F |
Ciąg 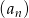 określony jest wzorem
określony jest wzorem 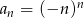 dla
dla 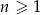 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 232 B) 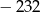 C) 96 D)
C) 96 D)